基于贝叶斯原理的复杂试验不确定度评定方法与流程

本发明涉及一种机械工程试验，特别涉及一种基于贝叶斯原理的复杂试验不确定度评定方法。

背景技术：

随着机械工业的发展，人们对产品质量的要求越来越高，因此很多产品均需进行相关试验来检验产品的合格性和可靠性。而这些试验很多都是复杂试验，复杂试验的一般特征是试验结果的影响因素众多，各因素的微小变动都将造成试验结果的不确定性，若试验结果的不确定性没有明确的度量标准，将使试验结果的可信度降低。因此，需要研究针对复杂试验结果不确定度分析方法，以提高试验结果的可信度。

目前常用的不确定度评定方法是由《测量不确定度指南》(gum)提出的a类和b类评定。但是当测量模型是复杂的非线性系统，且样本数不多时，采用gum方法对测量不确定度进行评价将导致结果不准确。而基于贝叶斯原理的不确定度评价方法能够充分利用现有信息、样本信息、经验信息等，将统计推断建立在实验分布的基础上，特别适用于小样本试验不确定度的评定。因此针对复杂非线性系统试验测量不确定度的评定，采用基于贝叶斯原理的试验测量不确定度评价将得到更加合理的结果。

技术实现要素：

本发明是针对对于要依赖复杂试验来验证产品品质的复杂试验的可靠性的问题，提出了一种基于贝叶斯原理的复杂试验不确定度评定方法，在复杂试验给出试验结果的同时，能够给出其试验不确定度，并对实验结果进行评价，从而制定实验改进方案。

本发明的技术方案为：一种基于贝叶斯原理的复杂试验不确定度评定方法，具体包括如下步骤：

1)、确定复杂试验被测量y，以及主要影响因素x＝[x1,x2,...,xn]；

2)、获得复杂试验影响因素xi的概率密度分布函数gxi(ξi)，ξi为影响因素的测量值；

3)、采用拉丁超立方抽样方法根据影响因素的概率密度函数gxi(ξi)进行试验抽样，得到影响因素的试验设计表dn，根据设计表的参数进行试验，得到各输入参数下复杂试验的结果yi；

4)、基于贝叶斯原理对复杂试验的不确定度进行评价：

4.1)以步骤3)试验结果yi的部分数据作为先验样本，另一部分作为当前测量样本；

4.2)计算先验样本的均值μ0和均值的标准差τ，以及当前测量样本的均值和标准差s；

4.3)利用所示公式计算被测量真值的估计

其中n为当前测量样本总数；

4.4)利用所示公式计算标准不确定度σ

4.5)由得到的被测量真值的估计和标准不确定度σ计算对应包含概率p的包含区间[ylow,yhigh]，其中ylow和yhigh计算分别为区间中最小值与最大值；

5)、输出步骤4.4)和4.5)结果作为不确定度评定。

本发明的有益效果在于：本发明基于贝叶斯原理的复杂试验不确定度评定方法，在复杂试验给出试验结果的同时，能够给出其试验不确定度，根据此对实验结果进行评价，从而制定实验改进方案。提高产品检验水平的同时保证品质要求高产品的质量。

附图说明

图1为本发明基于贝叶斯原理的复杂试验不确定度评定方法流程图；

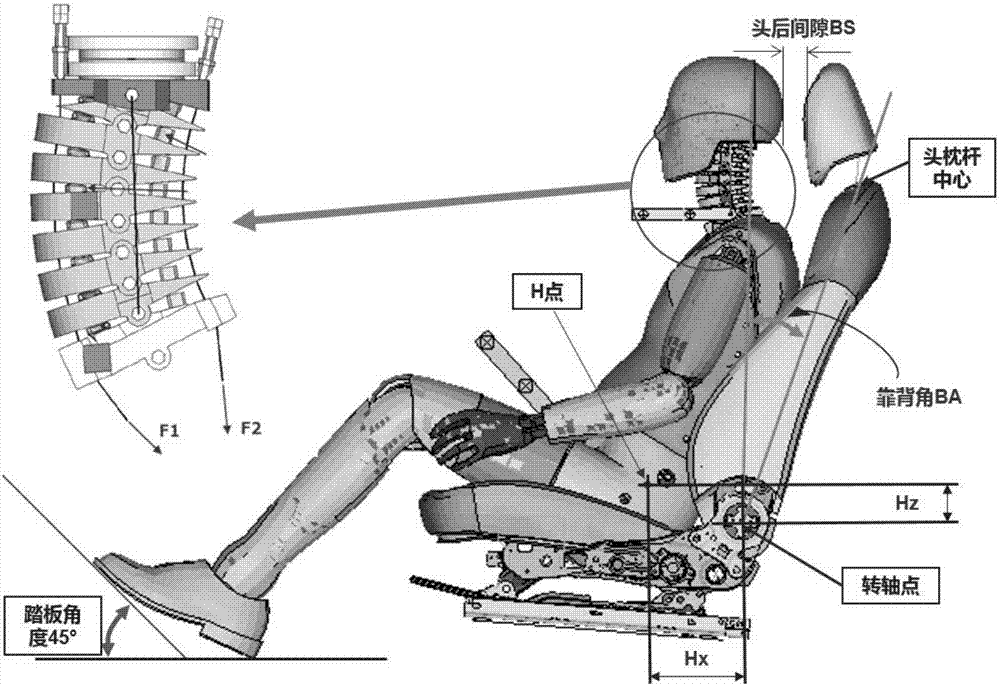
图2为本发明鞭打试验主要影响因素示意图；

图3为本发明h点x轴坐标概率密度分布函数图；

图4为本发明h点z轴坐标概率密度分布函数图；

图5为本发明头后间隙bs概率密度分布函数图；

图6为本发明座椅靠背角ba概率密度分布函数图；

图7为本发明f1的分布概率密度函数图；

图8为本发明f2的分布概率密度函数图。

具体实施方式

如图1所示基于贝叶斯原理的复杂试验不确定度评定方法流程图，具体方案如下：

1、确定复杂试验被测量y，以及主要影响因素x＝[x1,x2,...,xn]。

2、获得复杂试验影响因素xi的概率密度分布函数gxi(ξi)，ξi为影响因素的测量值。

3、采用拉丁超立方抽样方法根据影响因素的概率密度函数gxi(ξi)进行试验抽样，得到影响因素的试验设计表dn，根据设计表的参数进行试验，得到各输入参数下复杂试验的结果yi。

4、基于贝叶斯原理对复杂试验的不确定度进行评价：

4.1以步骤3试验结果yi的部分数据作为先验样本，另一部分作为当前测量样本。

4.2计算先验样本的均值μ0和均值的标准差τ，以及当前测量样本的均值和标准差s。

4.3利用所示公式(1)计算被测量真值的估计

其中n为当前测量样本总数

4.4利用所示公式(2)计算标准不确定度σ

4.5由得到的被测量真值的估计和标准不确定度σ计算对应包含概率p的包含区间[ylow,yhigh]，其中ylow和yhigh计算分别为区间中最小值与最大值。

5、输出4.4和4.5结果作为不确定度评定。

本发明以某一型号的汽车座椅鞭打试验评分不确定度评定进行说明，具体步骤如下：

(1)确定鞭打试验主要影响因素。

如图2所示鞭打试验主要影响因素示意图，选取对鞭打试验评分影响较大的影响因素，包括座椅本身参数的靠背角ba，假人本身参数的颈部预紧力f1和颈部预紧力f2，安装参数的假人h点相对转轴点x轴坐标差hx、假人h点相对转轴点z轴坐标差hz和头后间隙bs。

(2)各影响因素概率密度分布的确定。

根据历史数据对各输入参数进行统计，得出如图3所示h点x轴坐标概率密度分布函数图、如图4所示h点z轴坐标概率密度分布函数图、如图5所示头后间隙bs概率密度分布函数图，三者均符合正态分布，如图6所示座椅靠背角ba概率密度分布函数图，符合矩形分布。

正态分布函数的一般表达式如式(3)所示，记为其概率密度函数为正态分布的期望值θ决定了其位置，其标准差决定了分布的幅度。

在本次示例中，假人h点相对转轴点x轴坐标差hx的标准值为216.06，假人h点相对转轴点z轴坐标差hz的标准值为53.78，头后间隙bs的标准值为27。经过对数据进行处理后得出h点x轴坐标、h点的z轴坐标、头后间隙、座椅靠背角的概率密度函数分别如式(4)-(7)所示。

hx～n(216.21，1.2378²)(4)

hz～n(46.30，4.0527²)(5)

bs～n(26.89，0.7377²)(6)

ba～u(14.5，19.5)(7)

假人颈部预紧力由于没有传感器，不能通过历史数据得出，只能通过标定试验仿真得出其分布。通过改变f1和f2的值进行多次标定仿真试验，得出假人标定合格的条件是f1的取值范围要在(33.51,82.68)n的范围内，f2的取值范围要在(99.48,166.04)n的范围内。根据标定试验历史数据统计出各输出项的概率密度分布均符合正态分布，由此推论出在标定实验中的可调参数假人颈部预紧力f1与f2也符合正态分布规律。若考虑到f195％的置信区间为(33.51,82.68)，f295％的置信区间为(99.48,166.04)，可得到f1和f2的分布概率密度函数分别表示为(8)和(9)，对应概率分布密度函数如图7和图8所示。

f1～n(58.095，12.543²)(8)

f2～n(132.76，16.98²)(9)

(3)拉丁超立方抽样方法设计鞭打试验。

鞭打试验的目的是测试座椅对乘员颈部的保护效果，而针对某一具体型号的座椅对其进行试验的次数较少，直接利用测试结果进行不确定度评价将造成结果的不精确。因此需利用有限元代替物理试验来进行大量试验的方法来对该型号座椅鞭打试验不确定度进行评价。此时试验设计参数应符合概率密度分布，因此采用拉丁超立方抽样方法对设计参数进行抽样选取，该抽样方法属于分层抽样，得到的样本符合其概率密度分布，且能布满整个设计空间。在本次示例中选取的试验次数n为50次，抽样结果见附表1，由附表1的设计参数得到的试验结果，如表2所示鞭打试验有限元仿真评分结果。

表1

表2

(4)基于贝叶斯原理的不确定度评定。

贝叶斯方法是一种基于统计学理论的推断方法，它能充分利用现有信息、样本信息、经验信息等，建立贝叶斯不确定度评定模型，最后通过后验分布得到试验不确定度。具体评定步骤如下：

4.1)选取仿真试验前30组作为先验样本，后20组数据作为当前样本。

4.2)计算先验样本的均值和均值的标准差由于评分结果属于正态分布，则均值μ的先验密度函数为：

式中：nf为先验测量样本的总数，yi^f为先验测量样本的测量值。

4.3)计算当前样本的均值和标准差则当前样本的联合密度函数(似然函数)为

式中：n为当前测量样本的总数，yj为当前测量样本的测量值。

4.4)根据贝叶斯推断h(μ|y)∝p(μ)l(μ|y)可得后验分布

式中

由此计算可得出被测量真值的估计以及标准不确定度σ。

4.5)由得到的被测量真值的估计和标准不确定度σ计算对应包含概率p＝1-α的包含区间[ylow,yhigh]。

其中zα/2可通过查询标准正态分布函数表得到，其中zα/2在标准正态分布函数表中代表临界值，α是分位点。

(5)不确定度评定结果。

根据步骤(4)所示评定方案以及附表2的试验结果计算出先验样本的均值μ0＝3.8573和均值的标准差τ＝0.0626；当前样本的均值和标准差s＝0.2520；最后计算出的后验分布的估计值和标准不确定度σ，并得到对应于不同包含概率p的包含区间[ylow,yhigh]，具体分析结果如下表3所示基于贝叶斯理论的鞭打试验评分不确定度分析结果。

表3