一种弹性边界条件下拉索弯曲振动频率的求解方法与流程

本发明涉及一种拉索弯曲振动频率的求解方法，尤其是涉及一种弹性边界条件下拉索弯曲振动频率的求解方法。

背景技术

目前，为了保证桥梁的安全使用，通常需要对桥梁的各项指标进行监测。而拉索的弯曲振动作为桥梁工程的重要监测指标之一，通常假设拉索两端的边界条件为理想的固支或简支条件来计算得到拉索的振动频率。然而，事实上，拉索两端的边界条件并非理想的简支和固支，而是介于简支和固支之间，例如斜拉桥拉索的端部是通过锚具与主梁和索塔相连接的，在工程中锚具方式较为复杂，将拉索两端的边界条件假定为固支或简支边界，这种假定与实际边界约束存在较大的误差，由此导致得到的拉索弯曲振动频率存在较大的误差，准确度不高。

技术实现要素：

本发明所要解决的技术问题是提供一种准确度较高的弹性边界条件下拉索弯曲振动频率的求解方法。

本发明解决上述技术问题所采用的技术方案为：一种弹性边界条件下拉索弯曲振动频率的求解方法，包括以下步骤：

(1)获取待检测拉索的性能参数并基于获取到的拉索的性能参数构建拉索振动偏微分方程：

式(1)中，x表示待检测拉索的振动位移，x∈[0,l]，l表示待检测拉索的长度，t表示待检测拉索的索力的设计值，e表示待检测拉索的弹性模量，i表示待检测拉索的截面惯性矩，ρ表示待检测拉索的密度，a表示待检测拉索的截面积，t表示待检测拉索的振动时间，u(x,t)表示待检测拉索的各点随时间t变化的位移函数，表示u(x,t)对时间t求二阶偏导数；表示u(x,t)对x求二阶偏导数，表示u(x,t)对x求四阶偏导数；

(2)采用分离变量法对步骤(1)构建的拉索振动偏微分方程进行化简，具体化简过程为：

a.将u(x,t)分解为时间函数和空间函数间的乘积关系，得到：

式(2)中y(x)为拉索的振型函数，sin(*)为正弦函数，ω为拉索的振动频率，为拉索振动的相位角；

b.将式(2)代入式(1)中得到拉索振动微分方程：

eiy⁽⁴⁾(x)-ty⁽²⁾(x)-ρaω²y(x)＝0(3)

其中，y⁽⁴⁾(x)表示y(x)对x求四阶导数，y⁽²⁾(x)表示y(x)对x求二阶导数；

(3)建立拉索振动的弹性边界条件：

c.假设拉索的左端分别连接有弹性刚度为k1的拉伸弹簧和弹性刚度为k2的扭转弹簧，拉索的右端分别连接有弹性刚度为k3的拉伸弹簧和弹性刚度为k4的扭转弹簧，由此得到：

式(4)中，u”'|x＝0表示在x＝0处u(x,t)对x求三阶偏导数，u|x＝0表示在x＝0处u(x,t)的函数值，u”|x＝0表示在x＝0处u(x,t)对x求二阶偏导数，u'|x＝0表示在x＝0处u(x,t)对x求一阶偏导数，u”'|x＝l表示在x＝l处u(x,t)对x求三阶偏导数，u|x＝l表示在x＝l处u(x,t)的函数值，u”|x＝l表示在x＝l处u(x,t)对x求二阶偏导数，u'|x＝l表示在x＝l处u(x,t)对x求一阶偏导数，k1为弹性刚度为k1的拉伸弹簧刚度无量纲化系数，k2为弹性刚度为k2的扭转弹簧刚度无量纲化系数，k3为弹性刚度为k3的拉伸弹簧刚度无量纲化系数，k4为弹性刚度为k4的扭转弹簧刚度无量纲化系数，k1，k2，k3和k4的取值分别为：

式(5)中，符号“/”为除运算符号；k1，k2，k3和k4的取值范围均为[0,10⁴]，且同时满足以下三个条件：一、k1，k2，k3和k4的取值不能同时为0；二、k1，k2，k3和k4的取值不能同时为10⁴；三、当k1和k3的取值同时为10⁴，且k2的取值为0时，k4的取值不能为10⁴，当k1和k3的取值同时为10⁴，k4的取值为0时，k2的取值不能为10⁴；

d.将(2)式代入(4)式中得到拉索的弹性边界条件为：

式(6)中：y”'|x＝0表示在x＝0处y(x)对x求三阶导数，y|x＝0表示在x＝0处y(x)的函数值，y”|x＝0表示在x＝0处y(x)对x求二阶导数，y'|x＝0表示在x＝0处y(x)对x求一阶导数，y”'|x＝l表示在x＝l处y(x)对x求三阶导数，y|x＝l表示在x＝l处y(x)的函数值，y”|x＝l表示在x＝l处y(x)对x求二阶导数，y'|x＝l表示在x＝l处y(x)对x求一阶导数；

(4)将拉索的振型函数y(x)采用切比雪夫级数的形式进行展开，得到y(x)的展开式：

式(7)中：∑(*)表示对*进行求和，n为切比雪夫级数的最高阶，n为大于等于1的整数，i＝1，2，…，n；φi(x)为利用切比雪夫级数构造的满足边界条件式(6)的第i阶位移函数，ai为第i阶位移函数φi(x)的系数，为待定系数，其中

φi(x)＝h(x)ti(x)+g(x)(8)

其中，ti(x)为第i阶切比雪夫级数，h(x)和g(x)为构造的辅助函数，ti(x)的表达式为：

式(9)中：cos(*)表示余弦函数，arccos(*)表示反余弦函数；

h(x)和g(x)的表达式分别表示如下：

(5)根据虚位移原理令拉索在虚位移δy(x)上所作的功为零，其中δ表示变分，δy(x)的表达式为：

拉索在虚位移δy(x)上所作的功：

根据式(12)和式(13)，可以得到：

其中φi⁽⁴⁾(x)表示φi(x)对x求四阶导数，φi⁽²⁾(x)表示φi(x)对x求二阶导数，φj(x)表示第j阶位移函数，j＝1，2，…，n；整理式(14)后可得方程：

式(15)中：

将式(15)写成矩阵形式，即为拉索振动的特征方程：

(d-ω²m)h＝0(16)

式(16)中，d表示刚度矩阵，m表示质量矩阵，h表示系数矩阵，dij表示矩阵d的第i行第j列元素，mij表示矩阵m的第i行第j列元素，即：

(6)求解拉索振动的特征方程式(16)，得到频率方程为：

|d-ω²m|＝0(17)

其中|*|表示矩阵*的行列式，对频率方程(17)进行求解得到不同边界约束条件下拉索的振动频率ω。

与现有技术相比，本发明的优点在于首先通过获取待检测的拉索的性能参数并基于获取到的拉索的性能参数构建拉索振动偏微分方程，然后采用分离变量法对拉索振动偏微分方程进行化简，得到拉索振动微分方程，建立拉索振动的弹性边界条件，该弹性边界条件中排除了拉索左右两端的边界条件均为固支(k1，k2，k3和k4的取值同时为10⁴)的情况、拉索左右两端处于自由状态(k1，k2，k3和k4的取值同时为0)的情况、拉索左右两端的边界条件均为简支(当k1和k3的取值同时为10⁴时，k2和k4的取值同时为0)的情况、拉索左右两端的边界条件为固支-简支(当k1和k3的取值同时为10⁴，k2的取值为10⁴，k4的取值为0)的情况以及拉索左右两端的边界条件为简支-固支(当k1和k3的取值同时为10⁴，k2的取值为0，k4取值为10⁴)的情况，使拉索的左右两端边界条件为：简支-弹性边界、弹性-简支边界、固支-弹性边界、弹性-固支边界和弹性-弹性边界中的一种，然后将拉索的振型函数采用切比雪夫级数的形式进行展开，接着基于拉索的振型函数和弹性边界条件得到拉索振动的特征方程，最后基于拉索振动的特征方程得到拉索的频率方程，求解该频率方程得到拉索的振动频率，本发明的方法中，拉索的频率方程为弹性边界约束条件下拉索弯曲振动的模型，同时考虑了弯曲刚度和不同边界约束对拉索弯曲振动频率的影响，并且采用chebyshev多项式的方法(即切比雪夫级数)对拉索振形函数进行逼近，进一步提高测量结果的精确性和收敛性，获取到准确度较高的拉索振动频率。

附图说明

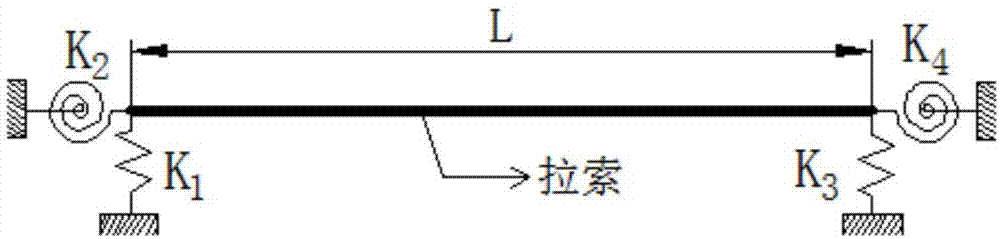
图1为本发明构建的弹性边界条件的实现结构。

具体实施方式

以下结合附图实施例对本发明作进一步详细描述。

实施例：一种弹性边界条件下拉索弯曲振动频率的求解方法，包括以下步骤：

(1)获取待检测拉索的性能参数并基于获取到的拉索的性能参数构建拉索振动偏微分方程：

式(1)中，x表示待检测拉索的振动位移，x∈[0,l]，l表示待检测拉索的长度，t表示待检测拉索的索力的设计值，e表示待检测拉索的弹性模量，i表示待检测拉索的截面惯性矩，ρ表示待检测拉索的密度，a表示待检测拉索的截面积，t表示待检测拉索的振动时间，u(x,t)表示待检测拉索的各点随时间t变化的位移函数，表示u(x,t)对时间t求二阶偏导数；表示u(x,t)对x求二阶偏导数，表示u(x,t)对x求四阶偏导数；

(2)采用分离变量法对步骤(1)构建的拉索振动偏微分方程进行化简，具体化简过程为：

a.将u(x,t)分解为时间函数和空间函数间的乘积关系，得到：

式(2)中y(x)为拉索的振型函数，sin(*)为正弦函数，ω为拉索的振动频率，为拉索振动的相位角；

b.将式(2)代入式(1)中得到拉索振动微分方程：

eiy⁽⁴⁾(x)-ty⁽²⁾(x)-ρaω²y(x)＝0(3)

其中，y⁽⁴⁾(x)表示y(x)对x求四阶导数，y⁽²⁾(x)表示y(x)对x求二阶导数；

(3)建立拉索振动的弹性边界条件，如图1所示：

c.假设拉索的左端分别连接有弹性刚度为k1的拉伸弹簧和弹性刚度为k2的扭转弹簧，拉索的右端分别连接有弹性刚度为k3的拉伸弹簧和弹性刚度为k4的扭转弹簧，由此得到：

式(4)中，u”'|x＝0表示在x＝0处u(x,t)对x求三阶偏导数，u|x＝0表示在x＝0处u(x,t)的函数值，u”|x＝0表示在x＝0处u(x,t)对x求二阶偏导数，u'|x＝0表示在x＝0处u(x,t)对x求一阶偏导数，u”'|x＝l表示在x＝l处u(x,t)对x求三阶偏导数，u|x＝l表示在x＝l处u(x,t)的函数值，u”|x＝l表示在x＝l处u(x,t)对x求二阶偏导数，u'|x＝l表示在x＝l处u(x,t)对x求一阶偏导数，k1为弹性刚度为k1的拉伸弹簧刚度无量纲化系数，k2为弹性刚度为k2的扭转弹簧刚度无量纲化系数，k3为弹性刚度为k3的拉伸弹簧刚度无量纲化系数，k4为弹性刚度为k4的扭转弹簧刚度无量纲化系数，k1，k2，k3和k4的取值分别为：

式(5)中，符号“/”为除运算符号；k1，k2，k3和k4的取值范围均为[0,10⁴]，且同时满足以下三个条件：一、k1，k2，k3和k4的取值不能同时为0；二、k1，k2，k3和k4的取值不能同时为10⁴；三、当k1和k3的取值同时为10⁴，且k2的取值为0时，k4的取值不能为10⁴，当k1和k3的取值同时为10⁴，k4的取值为0时，k2的取值不能为10⁴；d.将(2)式代入(4)式中得到拉索的弹性边界条件为：

式(6)中：y”'|x＝0表示在x＝0处y(x)对x求三阶导数，y|x＝0表示在x＝0处y(x)的函数值，y”|x＝0表示在x＝0处y(x)对x求二阶导数，y'|x＝0表示在x＝0处y(x)对x求一阶导数，y”'|x＝l表示在x＝l处y(x)对x求三阶导数，y|x＝l表示在x＝l处y(x)的函数值，y”|x＝l表示在x＝l处y(x)对x求二阶导数，y'|x＝l表示在x＝l处y(x)对x求一阶导数；

(4)将拉索的振型函数y(x)采用切比雪夫级数的形式进行展开，得到y(x)的展开式：

式(7)中：∑(*)表示对*进行求和，n为切比雪夫级数的最高阶，n为大于等于1的整数，i＝1，2，…，n；φi(x)为利用切比雪夫级数构造的满足边界条件式(6)的第i阶位移函数，ai为第i阶位移函数φi(x)的系数，为待定系数，其中

φi(x)＝h(x)ti(x)+g(x)(8)

其中，ti(x)为第i阶切比雪夫级数，h(x)和g(x)为构造的辅助函数，ti(x)的表达式为：

式(9)中：cos(*)表示余弦函数，arccos(*)表示反余弦函数；

h(x)和g(x)的表达式分别表示如下：

(5)根据虚位移原理令拉索在虚位移δy(x)上所作的功为零，其中δ表示变分，δy(x)的表达式为：

拉索在虚位移δy(x)上所作的功：

根据式(12)和式(13)，可以得到：

其中φi⁽⁴⁾(x)表示φi(x)对x求四阶导数，φi⁽²⁾(x)表示φi(x)对x求二阶导数，φj(x)表示第j阶位移函数，j＝1，2，…，n；整理式(14)后可得方程：

式(15)中：

将式(15)写成矩阵形式，即为拉索振动的特征方程：

(d-ω²m)h＝0(16)

式(16)中，d表示刚度矩阵，m表示质量矩阵，h表示系数矩阵，dij表示矩阵d的第i行第j列元素，mij表示矩阵m的第i行第j列元素，即：

(6)求解拉索振动的特征方程式(16)，得到频率方程为：

|d-ω²m|＝0(17)

其中|*|表示矩阵*的行列式，对频率方程(17)进行求解得到不同边界约束条件下拉索的振动频率ω。