一种线性高阶比例制导系统脱靶量的幂级数解的制作方法

本发明提供了一种线性高阶比例制导系统脱靶量的幂级数解，属于航天技术、武器技术领域。

背景技术

比例导引是最经典的制导律，由于其简洁、有效和易于物理实现，目前世界上战术导弹几乎都采用比例导引制导。导弹通常包含导引头、弹体环节、自动驾驶仪等系统，数学上最简化的导弹制导系统也要三阶微分方程来描述，很难得到这些高阶微分方程的解析解(有限项初等函数显示表示)，所以一般采用计算机数值仿真的方法来研究比例导引制导系统。

脱靶量是衡量导弹拦截目标或者目标逃逸策略的最重要最直观的性能指标，也是设计分析制导系统的关键核心。利用伴随法进行数值仿真是评估导弹系统设计和求解脱靶量的通用方法。对于线性一阶比例导引制导系统，当有效导引比为正整数时，利用伴随方程可直接得到脱靶量的解析解；但是对于一般的高阶制导系统，并不存在脱靶量的解析解。

幂级数法是求解常微分方程组的有效手段，通常先假设微分方程的解为系数待定的收敛的幂级数，然后将其代入微分方程，利用幂级数恒等条件，得到待定系数序列的递推关系；通常还要求出该幂级数的收敛半径，以确定幂级数解的适用区间。幂级数法在求解特殊线性微分方程、非线性微分方程和实际工程问题中都有重要应用。但是利用幂级数法来研究比例制导系统的工作还很少。

技术实现要素：

本发明的目的是提供一种线性高阶比例制导系统脱靶量的幂级数解，以填补现有技术中利用幂级数法来研究比例制导系统的空白。

本发明首先建立通用的线性高阶比例导引制导系统模型，由伴随构造得到相应的伴随系统，并对伴随系统的状态量和输出量(即脱靶量)进行无量纲化或归一化。假设伴随系统的状态量和脱靶量为幂级数和指数函数乘积的形式，得到幂级数系数的递推关系，并求出了幂级数解的收敛半径。由于脱靶量幂级数解是无穷级数表示的精确解，但实际应用中只能取级数的部分和来近似计算，还分析了参数对一般高阶制导系统幂级数解收敛速度的影响，并给出了参数的选择方案，从而得到了脱靶量的幂级数解。

本发明为一种线性高阶比例制导系统脱靶量的幂级数解，它包括以下三个步骤：

步骤一：线性高阶比例制导系统建模；

考虑一般的线化比例导引制导系统，研究目标阶跃机动和导弹初始瞄准误差角引起的脱靶量。伴随系统的微分方程为：

其中，n为有效导引比，t表示剩余飞行时间或总的飞行时间；z1、z2、zu和ζ是伴随系统的状态量，其初值分别为z1(0)＝1、z2(0)＝0、zu(0)＝0和ζ(0)＝0，其中z1的初值为1是由伴随系统的脉冲输入转化而来。伴随系统的输出量，即脱靶量为

其中，nt为目标机动水平大小，vm为导弹速度，θhe为导弹初始瞄准误差角；mnt表示目标阶跃机动引起的脱靶量，mhe表示导弹初始瞄准误差角引起的脱靶量。

g(s)为表征制导系统动态特性的稳定传递函数，包含导引头动力学、噪声滤波、飞控系统等环节；通常g(s)可以表示成如下形式

其中，q为制导系统阶数，t为参考时间常数或总制导系统时间常数，λq(q＝0,1,...q)是多项式系数。

进一步，将伴随系统的微分方程进行无量纲化，以得到归一化的脱靶量便于应用。引入如下无量纲变量，将伴随系统的状态量、脱靶量以及时间变量转化为无量纲和归一化变量：

传递函数替换为：

因此，为了简化表达式，如无特别说明，后文中无量纲或归一化的变量仍使用原变量符号，方程的求解和结果讨论都是针对无量纲化的变量。

步骤二：求解伴随系统的微分方程的幂级数解；包括求解幂级数解系数递推公式和幂级数收敛半径。

1.幂级数解的系数递推公式

假设无量纲方程有如下形式的幂级数解

其中，an、bn、cn、dn分别为各级数的待定系数，e表示自然指数，参数k表示指数项衰减常数，可用来调节幂级数解整体收敛速度。注意ζ的级数解中含有t^q项，这是因为关于ζ动态是由传递函数g(s)来描述的，等价于如下微分方程

其中ζ^(q)表示变量ζ的q阶导数。

利用关于时间多项式各次幂的系数相等，并结合伴随系统的微分方程的状态初值，可以得到如下递推关系

当n≥1时，

其中

这里bn和pn都是中间变量，用于简化表达式书写；a和c及其上下标表示排列数和组合数。cn和dn分别是归一化脱靶量mhe和mnt幂级数的系数。

2.幂级数解的收敛半径

首先求k＝0时，幂级数的收敛半径，其中an,0代表k＝0时幂级数系数an的值。

记状态向量

则伴随系统的微分方程可以写成如下状态空间描述

其中

式中，oq×1，oq×q，o1×q分别代表q行1列，q行q列，1行q列的零矩阵。

以及状态初值

x(0)＝[000...01]^t

显然，矩阵r的特征值只有0，任何正整数都不是r的特征值；函数矩阵a(t)是常值矩阵，在t＝0处是解析的，而且其幂级数展开收敛半径为无穷大，则可得，上述微分方程的解可以表示为收敛半径为无穷大的幂级数

其中xn是向量值级数系数，维数与x相同。，利用幂级数恒等条件，可以得到递推关系

式中，i是大小为(q+1)×(q+1)的单位矩阵。

由此系数序列xn唯一确定。向量xn中最后一个分量是状态z1幂级数的系数，通过递推关系消掉xn其它分量，可以验证最后一个分量序列与幂级数递推关系在k＝0时所确定的序列an,0相同，由此可得k＝0时z1的级数是收敛的且收敛半径无穷大。

其次，证明k为任意数时，幂级数是收敛的。设当为任意数时，幂级数系数序列记为和级数正是k＝0时收敛的级数与e^kt的麦克劳林级数的柯西积：

级数和同理。所以，当为任意数时，幂级数仍然收敛。事实上，e^-kt麦克劳林级数收敛半径为无穷大，只要k取某一值幂级数解收敛，则k取其它值时相应的幂级数解仍收敛，且收敛半径相同。

步骤三：选择合适指数项衰减常数k；

前两个步骤得到了伴随系统的微分方程的幂级数解，解中包含一个指数项，其随时间的衰减速度由参数k决定，为了使幂级数解能够尽快收敛，需要进一步分析参数k对幂级数解收敛速度的影响，给出选取参数k的方案。

引入用来衡量幂级数解的收敛速度指标变量ncr，其意义是使得部分和逼近误差余式rn小于指定精度ε的索引变量n的最小值，换句话说，至少需要ncr+1项部分和，才会使得逼近精确解的误差小于ε；ncr与k有关，我们将ncr表示成关于k的函数形式

从定义可以看出ncr越小越好，意味着收敛速度越快。使得ncr取值最小的k是最优的，记为

同时考虑幂级数精度、收敛速度和递推关系的简化，可以按照如下方案选取参数k：一阶制导系统选取k＝1，欠阻尼二阶制导系统选取k＝ξ/β，q阶二项式系统选取k＝q，对于一般的高阶系统可选取

上述各式中，αi(i＝1,2,...q1)为一阶环节特征参数，ξj(j＝1,2,...q2)和βj(j＝1,2,...q2)为二阶环节特征参数。

而相应的部分和项数可由式(15)确定。

本发明的优点在于：

(1)推导了一般比例高阶制导系统脱靶量的幂级数解系数的递推关系；对于不同有效导引比、不同形式的高阶制导系统，幂级数解系数递推求解过程具有一致性。

(2)求出了幂级数的收敛半径并给出了指数型衰减常数的选取方案；利用收敛幂级数的部分和可以得到脱靶量解析的、形式统一的逼近公式。

(3)给出的幂级数解是脱靶量一种精确的解的形式，可以用来研究脱靶量的性质以及寻找某些特殊条件下的解析解。

附图说明

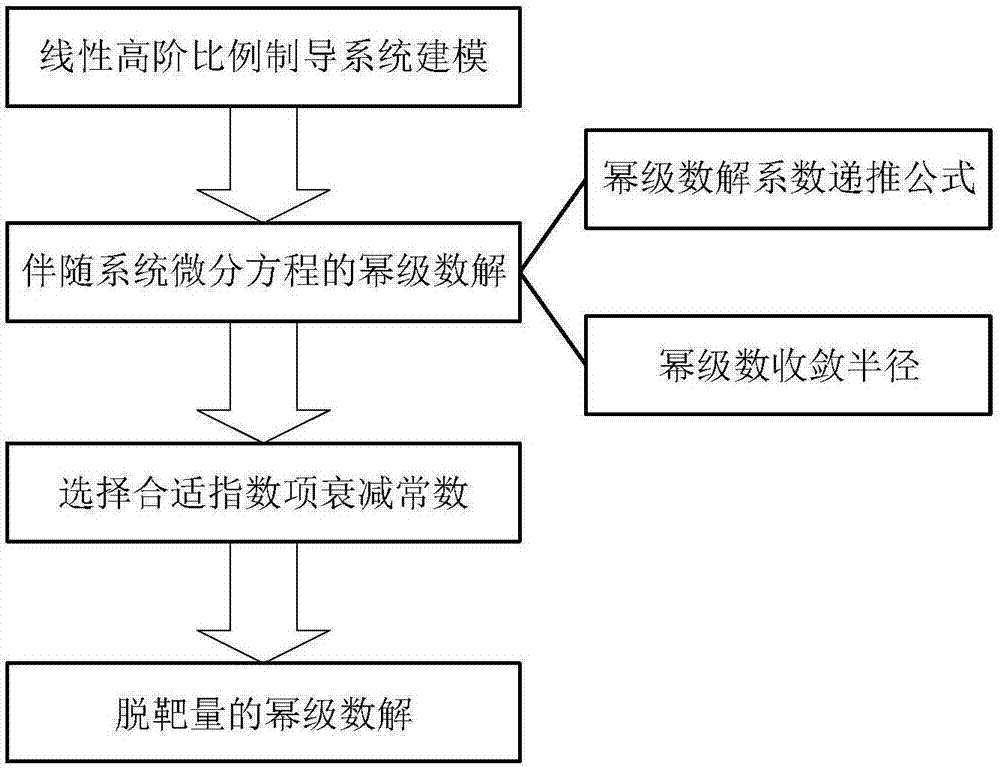
图1是本发明流程图。

图2是线性比例制导系统及其伴随系统框图。

图3a是k＝3时含有一个二阶环节的五阶制导系统目标阶跃机动脱靶量的伴随仿真结果与幂级数解部分和对比图。

图3b是k＝7时含有一个二阶环节的五阶制导系统目标阶跃机动脱靶量的伴随仿真结果与幂级数解部分和对比图。

图3c是k＝10时含有一个二阶环节的五阶制导系统目标阶跃机动脱靶量的伴随仿真结果与幂级数解部分和对比图。

图4a是t＝10，ε＝10^-4的一阶制导系统，不同的有效导引比n得到ncr(k)的曲线图。

图4b是n＝4，t＝10，ε＝10^-4的欠阻尼二阶制导系统，不同的阻尼比ξ得到ncr(k)的曲线图。

图4c是n＝4，t＝10，ε＝10^-4的欠阻尼二阶制导系统，不同的系统阶数q得到ncr(k)的曲线图。

图4d是n＝4，t＝10，ε＝10^-4的一般的五阶制导系统，时间常数分布不同的传递函数g(s)得到ncr(k)的曲线。

图4e是n＝4，t＝10的含有一个二阶环节的五阶制导系统，不同误差精度ε得到ncr(k)的曲线。

图4f是n＝4，t＝10的含有一个二阶环节的五阶制导系统，在不同时间t处得到ncr(k)的曲线。

图5a是二项式形式的五阶制导系统目标阶跃机动脱靶量的伴随仿真结果与幂级数解部分和对比图。

图5b是二项式形式的五阶制导系统初始瞄准误差脱靶量的伴随仿真结果与幂级数解部分和对比图。

图5c是各时间常数不等的一阶环节乘积形式的五阶制导系统目标阶跃机动脱靶量的伴随仿真结果与幂级数解部分和对比图。

图5d是各时间常数不等的一阶环节乘积形式的五阶制导系统初始瞄准误差脱靶量的伴随仿真结果与幂级数解部分和对比图。

图5e是含有一个二阶环节的五阶制导系统目标阶跃机动脱靶量的伴随仿真结果与幂级数解部分和对比图。

图5f是含有一个二阶环节的五阶制导系统初始瞄准误差脱靶量的伴随仿真结果与幂级数解部分和对比图。

上述图中，涉及到的符号、代号说明如下：

n为有效导引比，伴随系统中t表示剩余飞行时间或总的飞行时间，nt为目标机动水平大小，vm为导弹速度，θhe为导弹初始瞄准误差角；mnt表示目标阶跃机动引起的脱靶量，mhe表示导弹初始瞄准误差角引起的脱靶量。z1、z2、zu和ζ为伴随系统状态。

具体实施方式

下面将结合附图和实施案例对本发明作进一步的详细说明。

本发明为一种线性高阶比例制导系统脱靶量的幂级数解，包括三个步骤，具体流程如图1所示，下面我们具体介绍上述三个步骤。

步骤一：线性高阶比例制导系统建模；考虑一般的线化比例制导系统，研究目标阶跃机动和导弹初始瞄准误差角引起的脱靶量。图2给出了原线化比例制导系统以及其伴随系统的框图，则可得到如下伴随系统的微分方程：

其中，n为有效导引比，t表示剩余飞行时间或总的飞行时间；z1、z2、zu和ζ是伴随系统的状态量，其初值分别为z1(0)＝1、z2(0)＝0、zu(0)＝0和ζ(0)＝0，其中z1的初值为1是由伴随系统的脉冲输入转化而来。伴随系统的输出量，即脱靶量为

其中，nt为目标机动水平大小，vm为导弹速度，θhe为导弹初始瞄准误差角；mhe是由于导弹初始航向误差造成的脱靶量，mnt是由于目标造成的脱靶量。

g(s)表示一般的稳定传递函数，包含导引头动力学、噪声滤波、飞控系统等环节；通常g(s)可以表示成如下形式

即g(s)是由q1个一阶环节和q2个二阶环节组成，αi(i＝1,2,...q1)为一阶环节特征参数，ξj(j＝1,2,...q2)和βj(j＝1,2,...q2)为二阶环节特征参数，均为无量纲的正数；不失一般性，令

t为参考时间常数或总制导系统时间常数，具有时间的量纲。为了推导一般形式的脱靶量的解，将g(s)关于s分母多项式展开得到

其中q＝q1+2q2；λq(q＝1,2,...q)是多项式系数，由式(3)中的αi、ξj和βj唯一确定，结合式(4)可以得到

λ0＝1,λ1＝1(6)

进一步，将伴随系统的微分方程(1)和输出方程(2)进行无量纲化，以得到归一化的脱靶量便于应用。注意到脱靶量具有长度的量纲，由(2)可得z2具有时间的量纲，zu具有平方时间的量纲，z1和ζ无量纲；因此，引入如下无量纲变量，将时间变量、伴随系统的状态量和输出量(脱靶量)转化为无量纲和归一化变量：

经过简单求导运算可以得出，无量纲的伴随系统状态量关于无量纲的时间的微分方程与(1)相同，只需将传递函数替换为：

因此，为了简化表达式，如无特别说明，后文中无量纲或归一化的变量仍使用原变量符号，方程的求解和结果讨论都是针对无量纲化的变量。

步骤二：求解伴随系统的微分方程的幂级数解；包括求解幂级数解的系数递推公式和幂级数解的收敛半径。

1.幂级数解的系数递推公式

一般地，伴随系统的微分方程(1)不存在由有限项初等函数构成的解析解，但是当g(s)为一阶环节且有效导引比n为正整数时，利用laplace变换可以得到方程(1)解析解(归一化后结果)为

注意式(10)中解析解都是e指数与多项式函数乘积的形式，受此启发，当n不是正整数或者制导系统的阶数是高阶时，我们可以求解和探讨无量纲方程(1)如下形式的幂级数解

其中an、bn、cn、dn分别为各级数的待定系数，参数k表示指数项衰减常数，可用来调节幂级数解整体收敛速度。注意ζ的级数解中含有t^q项，这是因为关于ζ动态是由传递函数(9)来描述的，等价于如下微分方程

其中ζ^(q)表示变量ζ的q阶导数。对z1、ζ、z2和zu级数求导可得

其中a和c及其上下标分别表示排列数和组合数。

将式(11)及其相应的导数式(13)代入微分方程(1)和(12)，等号两侧的指数部分消掉，利用关于时间多项式各次幂的系数相等，并结合伴随系统状态量的初值，可以得到如下递推关系

当n≥1时，

其中

这里bn和pn都是中间变量，用于简化表达式书写；a和c及其上下标仍然表示排列数和组合数。cn和dn分别是归一化脱靶量mhe和mnt幂级数的系数。

2.幂级数解的收敛半径

首先求k＝0时，幂级数解的收敛半径。因为代表脱靶量的级数z2和zu可以由z1积分得到，故只需求解k＝0时z1的级数的收敛半径即可，其中an,0代表k＝0时幂级数系数an的值。

记状态向量

x＝[ζζ⁽¹⁾ζ⁽²⁾…ζ^(q-1)z1]^t(16)

则微分方程(1)和(11)可以写成如下状态空间描述

其中

式中，oq×1，oq×q，o1×q分别代表q行1列，q行q列，1行q列的零矩阵。

以及状态初值

x(0)＝[000…01]^t(20)

显然，矩阵r的特征值只有0，任何正整数都不是r的特征值；函数矩阵a(t)是常值矩阵，在t＝0处是解析的，而且其幂级数展开收敛半径为无穷大，则可得，微分方程(17)的解可以表示为收敛半径为无穷大的幂级数

其中xn是向量值级数系数，维数与x相同。将(21)代入(17)，利用幂级数恒等条件，可以得到递推关系

式中，i是大小为(q+1)×(q+1)的单位矩阵。

由此系数序列xn唯一确定。向量xn中最后一个分量是状态z1幂级数的系数，通过递推关系消掉xn其它分量，可以验证最后一个分量序列与递推关系(15)在k＝0时所确定的序列an,0相同，由此可得k＝0时z1的级数是收敛的且收敛半径无穷大。

其次，证明k为任意数时，由递推关系(14)和(15)所确定的幂级数(11)是收敛的。设当k为任意数时，由递推关系(14)和(15)得到的序列记为和容易验证

满足递推关系(14)和(15)，再由该递推关系生成的序列是唯一的，所以式(23)恒成立。仔细观察发现级数正是k＝0时收敛的级数与e^kt的麦克劳林级数的柯西积：

级数和同理。所以，当k为任意数时，幂级数(11)仍然收敛。事实上，e^-kt麦克劳林级数收敛半径为无穷大，只要k取某一值幂级数解收敛，则k取其它值时相应的幂级数解仍收敛，且收敛半径相同。

步骤三：选择合适指数项衰减常数k。

前两个步骤得到了伴随系统的微分方程的幂级数解，解中包含一个指数项，其随时间的衰减速度由参数k决定，为了使幂级数解能够尽快收敛，需要进一步分析参数k对幂级数解收敛速度的影响，给出选取参数k的方案。

首先来看一下不同参数k对同一制导系统幂级数解的影响，这里选取含有一个二阶环节的五阶制导系统

式中，α1＝0.1，α2＝0.2，α3＝0.56，ξ＝0.7，β＝0.1。

图3a、b、c给出了k分别取3、7和10时脱靶量幂级数解(部分和sn)与伴随仿真结果，算例中n＝4。

从图中可以看出，k＝7时大约需要60项部分和(即s60)就可以很好地逼近精确解，而k＝10时大约80项，k＝3时则要超过150项，k＝7时幂级数解收敛速度要快于k＝3和k＝10时。这可以从幂级数解zu的假设形式(13)来给出解释，具体地，zu是由常规幂级数和指数函数e-^kt乘积组成。当k较大时，指数函数随着t的衰减速度很快，部分和sn(t)中指数部分占主导(在n较小时)，比如k＝10时s60(t)的曲线在t＝8处就衰减到0附近，导致偏离脱靶量精确解。当k较小时，指数函数随着t的衰减速度要小于脱靶量精确解的实际衰减速度，而多项式在t较大时随着t的增大是发散的，此时部分和sn(t)中多项式部分在t较大处可能占主导，比如k＝3时s80(t)、s100(t)、s120(t)的曲线随着t的增加严重偏离脱靶量精确解。

我们讨论幂级数部分和sn来逼近脱靶量精确解的误差都是指截断误差，也就是余式rn，理论上，rn随着n的增加趋于0。为了进一步准确客观分析，引入用来衡量幂级数收敛速度指标变量ncr，其意义是使得部分和逼近误差余式rn小于指定精度ε的索引变量n的最小值，换句话说，至少需要ncr+1项部分和，才会使得逼近精确解的误差小于ε；ncr与k有关，我们将ncr表示成关于k的函数形式

从定义可以看出ncr越小越好，意味着收敛速度越快。使得ncr取值最小的k，是最优的，记为

注意ncr和kopt与整个制导系统的参数和分析条件有关，包括制导系统阶数、时间常数分布、有效导引比n和分析时间t、误差精度ε等。图4a～图4f给出了不同参数和条件下幂级数解收敛速度指标ncr(k)的曲线，为了保证数值精度，采用四精度甚至更高精度浮点数运算，并且用级数前1001项(足够精确了)部分和s1000(t)作为脱靶量精确解来计算余式，即rn(t)＝s1000(t)-sn(t)。

综上分析，同时考虑幂级数收敛速度和递推关系的简化，可以按照如下方案选取参数k：一阶制导系统选取k＝1，欠阻尼二阶制导系统选取k＝ξ/β，q阶二项式系统选取k＝q，对于一般的高阶系统可选取

上述各式中，αi(i＝1,2,...q1)为一阶环节特征参数，ξj(j＝1,2,...q2)和βj(j＝1,2,...q2)为二阶环节特征参数。

而相应的部分和项数可由式(26)确定。通常取值k大一些更好，这时不同制导系统收敛速度几乎相同，而且数值运算稳定性更好，避免双精度浮点数运算舍入误差累积发散；另外，k较大时系数序列dn在n充分大时同号，而且dn/dn-1随着n的增大单调趋于0，则对于任意小的正数q，存在正整数l，使得当n＞l时，有

利用此式我们可以得到简单的余式估计

这里t需要满足qt＜1。考虑到收敛速度，k取值一般不超过10。

实施案例

为了验证此幂级数解的精度，研究五阶制导系统，将数值仿真得到的脱靶量与其幂级数解进行对比。比例导引有效导引比n＝4，总飞行时间tf＝10s。

传递函数g(s)分别选取二项式形式：

各时间常数不等的一阶环节乘积形式：

其中，α1＝0.0667，α2＝0.133，α3＝0.2，α4＝0.267，α5＝0.333。

以及三个一阶环节和一个二阶环节乘积形式：

其中，α1＝0.1，α2＝0.2，α3＝0.56，ξ＝0.7，β＝0.1。由以上传递函数可知，总时间常数均为t＝1s。

对于传递函数g1(s)，指数项衰减常数取k＝5，目标阶跃机动引起的脱靶量和导弹初始瞄准误差引起的脱靶量的幂级数解部分和sn(t)与伴随仿真结果的对比分别如如图5a、b所示。随着n增加，部分和sn(t)都逐渐逼近脱靶量伴随仿真结果(或者精确解)，s40已经与伴随结果相差无几。

对于传递函数g2(s)，指数项衰减常数取k＝15，目标阶跃机动引起的脱靶量和导弹初始瞄准误差引起的脱靶量的幂级数解部分和sn(t)与伴随仿真结果的对比分别如如图5c、d所示。随着n增加，部分和sn(t)都逐渐逼近脱靶量伴随仿真结果(或者精确解)，s130已经与伴随结果相差无几。

对于传递函数g3(s)，指数项衰减常数取k＝10，目标阶跃机动引起的脱靶量和导弹初始瞄准误差引起的脱靶量的幂级数解部分和sn(t)与伴随仿真结果的对比分别如如图5e、f所示。随着n增加，部分和sn(t)都逐渐逼近脱靶量伴随仿真结果(或者精确解)，s90已经与伴随结果相差无几。