一种基于时态图的时间最小生成树的增量方法与流程

本发明涉及时态网络
技术领域：
，更具体地，涉及一种基于时态图的时间最小生成树的增量方法。
背景技术：
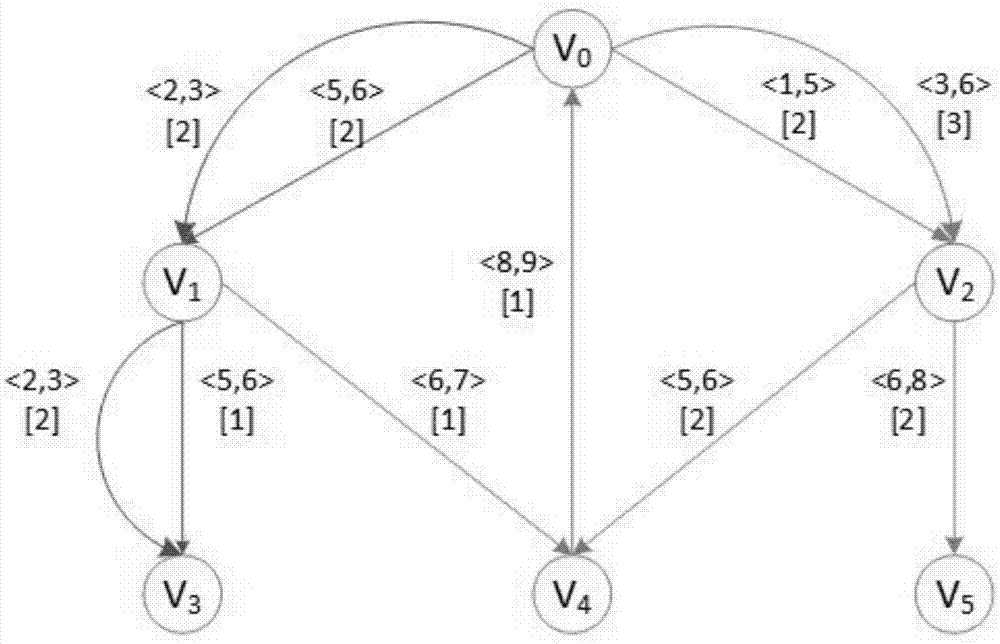
：近年来，各种大型网络越来越受到研究人员的重视。在以往，人们关注的大多是静态网络。但其实很多静态网络中都包含时间信息，这些时间信息对网络分析具有十分重要的意义，而这种带有时间信息的网络就称为时态网络。时态网络中一个重要的类型就是社交网络，其中每条边代表两个团体或者个体之间的一次联络。另一个常用于研究的类型是交通网络，每条边上的时间标签代表某项交通工具的出发和到达时间。还有很多其他时态网络的例子，比如大脑神经网络、经济网络等。考虑公交网络中行驶路线作为时态图的一个例子。每条行驶路线包含起始站点、到达站点、起始时间、到达时间和费用信息。可以用一个有向图g＝(v,e)来表示，其中e中的每条边e可以表示为(u,v,tu,tv,w)，其中e连接起始节点u和到达节点v，出发时间是tu，到达时间是tv，代价为w。在g中一条路径p是一些边的序列<e1,e2,…,ek>，k≤|v|，其中边ei的到达节点是边ei+1的起始节点。时态图中路径需要满足以下条件，ei+1的起始时间不小于ei的到达时间，领域内将这个条件称为时间约束。时间约束条件给研究带来了挑战。最小生成树问题是图论中的一个经典问题，它在现实中的应用也十分广泛。在社交网络中，最小生成树问题应用于信息传播、病毒营销、谣言传播等方面的研究；在公交路网中，最小生成树问题可以应用于路径规划、最优选址等问题的研究。而在时态图下，最小生成树也是一个十分重要的问题。根据时态图的特性，最小生成树可以分为基于时间最优的时间最小生成树和基于代价最优的代价最小生成树。下面主要考虑时间最优时间最小生成树。siluhuang、adawai-cheefu、ruifengliu在sigmod2015的论文minimumspanningtreesintemporalgraphs中给出了时态图g中时间最小生成树的求解方法。通过该方法，能够找到时态图的时间最小生成树。不过，已有方法变不支持动态变化的时态图。但是在现实情况中，时态图往往是动态变化的。比如公交网络，经常会发生公交线路增加、删除等情况。如果要在改变后的时态图中，查找新的时间最小生成树，一种简单的方法是重新运行一次原来的查找算法。然而，技术人员发现时间最小生成树往往只是图g的一小部分，尤其在图g很大，而对g的改变又比较小的时候更是明显，这个时候如果再去重新运行原算法就很不明智了，这是因为很多没有变化的边需要重新检测计算，效率变得很低下。如果技术人员可以对初始的最小生成树加以充分利用，并在时态图中寻找造成影响的部分，只对这部分进行计算就能够快速更新最小生成树。因此，本发明提供了时态图下时间最小生成树的增量算法，来快速更新时间最小生成树。技术实现要素：本发明针对时态图发生改变的情况，提出一种基于时态图的时间最小生成树的增量方法，对原来的最小生成树加以利用，快速找到新的最小生成树。为实现以上发明目的，采用的技术方案是：一种基于时态图的时间最小生成树的增量方法，包括增加边的情况和删除边的情况，包括以下内容：一、增加边的情况(1)根据原图g和变化δg更新图的存储结构，保持每个节点的出边按出发时间从大到小顺序；(2)判断插入的新边是否会对其到达节点v造成影响；如果不造成影响，那么不需要更新最小生成树msta，结束；如果造成影响，执行下一步；(3)更新a(v)和p(v)，a(v)更新为这条边的到达时间tv，p(v)更新为这条边的起始节点u；其中，p(v)表示在时间最小生成树中节点v的父亲节点，a(v)表示在时间最小生成树中点v的最早到达时间，然后按照v的出边邻接列表中的顺序扫描v的出边，若是新边满足时间约束的就加入栈s中；(4)取出栈s中的一条边，判断其是否会对这条边的到达节点造成影响；如果没有造成影响，则继续取栈s中的边，直到其有影响或栈s为空；如果造成了影响，执行下一步；(5)更新该节点的最早到达时间和其父节点；然后判断该节点的出边，新边满足时间约束则加入栈s；(6)循环步骤(4)、(5)直到栈s为空，即没有节点的最早到达时间改变；此时，时间最小生成树更新完毕；二、删除边的情况(1)先根据原图g和变化δg更新图的存储结构，保持每个节点的出边按出发时间从大到小顺序；(2)对δg中的所有边进行判断，如果是初始最小生成树msta中的边，则将该边的到达节点加入集合vs，并将在初始最小生成树msta中以这些点为根的子树中的点也加入到vs中；(3)对vs中的节点进行初始化，最早到达时间初始化为无穷大，父结点初始化为-1，pos值初始化为1(用pos(v)记录在v的出边中当前扫描的位置)；(4)将满足以下两个条件的边先放入栈s中：(i)这条边的起始节点不在集合vs中，到达节点在集合vs中；(ii)这条边满足时间约束，即这条边的出发时间大于该边起始节点的a值；(5)取出栈s中的一条边，判断其是否会对这条边的到达节点造成影响；如果没有造成影响，则继续取栈s中的边，直到其有影响或栈s为空；如果造成了影响，执行下一步；(6)根据这条边更新该节点的最早到达时间和其父节点，即a和p值，a值更新为这条边的到达时间，p值更新为这条边的起始节点；然后判断该节点的出边，满足时间约束则加入栈s；(7)循环步骤(5)和(6)，直到栈s为空，即没有节点的最早到达时间改变；此时，时间最小生成树更新完毕。优选地，所述第二部分删除边的步骤(2)中，将节点加入到vs中后，对vs中的节点进行剪枝处理：(1)用vd表示删除边的目的节点集，且按节点在初始msta中的层数由大到小排列；(2)如果从根节点r到节点v的路径上包含vd中的其他节点，对vs中节点v和它的子孙节点进行标记；如果从根节点r到节点v的路径上不包含vd中的其他节点，执行下一步；(3)对v进行标记；(4)估算v的新的最早到达时间值，将估算值表示a′(v)；(5)检查v的最到达时间估算值a′(v)是否会对v的未标记的孩子节点造成影响，即判断在初始msta中，v到它的孩子节点的边是否还满足时间约束；如果不满足时间约束，说明会对该孩子节点造成影响，将以该孩子节点为根的子树中的点均标记；如果依然满足时间约束，说明对孩子不造成影响，那么不标记，以这些节点为根的子树可以进行剪枝，从vs中剔除这些节点；(6)当依次遍历完vs中所有节点后，vs中剩下被标记的节点就是剪枝后依然受影响的节点。优选地，所述时间最小生成树msta是一棵树t＝(vr,er)，其满足以下条件：(1)节点集vr包含图g中所有根节点r可到达的节点；(2)且v≠r，v都只有一条入边，r没有入边；(3)且v≠r，从r到v的路径p(r,v)使得点v的到达时间最早，节点v的最早到达时间用a(v)表示。附图说明图1时态图g的示意图。图2时态图g的时间最小生成树的示意图。图3时态图g增加边的示意图。图4时态图g增加边后的时间最小生成树的示意图。图5时态图g删除边的示意图。图6时态图g删除边后的时间最小生成树的示意图。图7时态图最小生成树的示意图。具体实施方式附图仅用于示例性说明，不能理解为对本专利的限制；以下结合附图和实施例对本发明做进一步的阐述。实施例1本发明是针对时态图发生改变的情况，提出一种基于时态图的时间最小生成树的增量方法，对原来的最小生成树加以利用，快速找到新的最小生成树。首先给出本发明的相关定义：定义1(时态图)：给定一个时态图g＝(v,e)，其中v是时态图的节点集，e是时态图的边集。边e用一个五元组来表示，即e＝(u,v,tu,tv,w)，其中u是边e的起始节点，v是边e的到达节点，tu是边e的出发时间，tv是边e的到达时间，w是这条边的代价。本发明称节点u是节点v的一个前驱节点，节点v是节点u的一个后继节点。同时，为了下面叙述方便，边e的起始节点、到达节点、出发时间、到达时间、代价也可以分别表示为e.u、e.v、e.tu、e.tv、e.w。例子1：图1是一个是时态图，节点集v＝{v0,v1,v2,v3,v4,v5}，其中边e＝(v0,v1,2,3,2)是图中的一条边，表示这条边在时间2从节点v0出发，在时间3到达节点v1，代价为2。该图中v1的入边是(v0,v1,2,3,2)和(v0,v1,5,6,2)；v1的出边是(v1,v3,2,3,2)、(v1,v3,5,6,1)和(v1,v4,6,7,1)。所以v1的前驱节点是v0，v1的后继节点是v3和v4。定义2(路径)：时态图g＝(v,e)中的路径指的是一个边序列p＝<e1,e2,…,ek>，ei的到达节点是ei+1的起始节点，且ei的到达时间不大于ei+1的出发时间(1≤i≤k)。本发明认为ei+1是满足时间约束的，所以才能和ei一起构成一条路径。同时，本发明用p(u,v)表示从节点u到节点v的路径。如果节点u到节点v存在一条路径，那么称从u到v是可达的。例子2：在图1所示的时态图中，p(v0,v3)表示从节点v0到节点v3的路径，此例中p(v0,v3)＝<(v0,v1,2,3,2),(v1,v3,5,6,1)>。定义3(时间最小生成树msta)：在时态图g中，给定一个根节点r，g的时间最小生成树msta是一棵树t＝(vr,er)，其满足以下条件：(1)节点集vr包含图g中所有根节点r可到达的节点；(2)且v≠r，v都只有一条入边，r没有入边；(3)且v≠r，从r到v的路径p(r,v)使得点v的到达时间最早，节点v的最早到达时间用a(v)表示。例子3:对于图1中的时态图，给定根节点为v0，图2所示是图1的时间最小生成树。该生成树中节点v1,v2,v3,v4,v5的最早到达时间分别是3,5,6,6,8.下面的定义4是本发明中关于时态图中时间最小生成树的增量问题的具体定义。定义4：已知一个时态图g＝(v,e)，根节点r，以及图g求得的初始时间最小生成树msta，增量问题就是当图g发生变化δg(即增加边δe+和删除边δe-)时，寻找一个算法tδ，来找到受影响节点，从而快速更新时间最小生成树，而算法tδ就是本发明中所提出的增量算法。为了方便后续的说明，本发明继续给出如下定义。定义5(受影响节点)：给定一个时态图，一个根节点r，及初始时间最小生成树，根据定义3，每个节点都会有个最早到达时间(如果不可达即为无穷大)，当图g发生变化δg时，图中最早到达时间发生变化或者在树中的父节点发生变化的节点称为受影响节点。为了解决时态图上时间最小生成树的增量问题，本发明提出了以下技术方案。本发明提出的增量算法关键在于对初始的时间最小生成树msta加以利用，使得在图g发生变化δg时，可以迅速更新时间最小生成树。siluhuang等人在sigmod2015上提出了一种算法来计算时态图上的时间最小生成树，其计算出的最小生成树即为初始msta。因为初始msta已知，所以对a(v)和p(v)已知，其中p(v)表示在初始msta中节点v的父亲节点。而初始的时态图g也是已知的，以邻接边列表格式存储，对任意一个节点v，将其所有出边按其出发时间非递增排序，用eo(v)存储v的所有出边，|eo(v)|即为节点v的出度。本发明将时态图上时间最小生成树的增量问题分成两部分来讨论：时态图g增加边和删除边两种情况。part1：增加边的情况这一部分讨论时态图g增加边的情况。本发明先以增加一条边为例进行介绍，下面部分增加的边用e＝(u,v,tu,tv,w)∈δe+表示，本发明先给出引理1。引理1：当且仅当增加的边e＝(u,v,tu,tv,w)中的到达时间tv小于a(v)，并且起始时间tu大于等于a(u)时(即tv<a(v)且tu≥a(u))，初始的时间最小生成树才会改变。证明：通过以下四种情况可以证明：(1)tv<a(v)且tu≥a(u)。根据定义2，可以知道p(r,u)∪e满足时间约束，是一条路径。因为新增加的边的到达时间tv小于初始msta中点v的最早到达时间a(v)，因此增加的这条边e应该替换初始msta中到达节点v的边。此时，初始msta发生变化。(2)tv≥a(v)且tu≥a(u)。此时，p(r,u)∪e虽然满足时间约束，但是因为tv>a(v)，说明这条路径到达节点v的时间并不是最早的。因此，初始msta不发生变化。(3)tv<a(v)且tu<a(u)。p(r,u)∪e不满足时间约束，不是一条路径，因此从节点r不能经过p(r,u)和e到达节点v。此时初始msta不发生变化。(4)tv≥a(v)且tu<a(u)。初始msta不发生变化，原因同(3)。根据引理1，当tv<a(v)且tu≥a(u)，那么e应该插入到msta中，代替初始msta中的到达节点v的边。此时可能出现以下情况：以v为起始节点的一些边在增加边e前，不满足时间约束，但是在增加边e后，因为v的最早到达时间a(v)变小，此时可满足时间约束。令vs表示受影响节点集，如果a(v)变小，则将v加入到vs中，并针对v的出边中新满足时间约束且到达时间更小的边，将其对对应的到达节点也加入vs中，对vs中每个新加入的节点都如此判断，迭代下去，直到没有新节点加入，就找到了本问题的受影响节点集。下面介绍具体更新时间最小生成树的步骤。(1)先根据原图g和变化δg更新图的存储结构，要保持每个节点出边按出发时间从大到小的顺序不变。(2)判断插入的新边是否会对其到达节点v造成影响(即v的到达最早到达时间是不是会变小)。如果不造成影响，那么不需要更新msta，结束；如果造成影响，执行下一步。(3)更新a(v)和p(v)，a(v)更新为这条边的到达时间tv，p(v)更新为这条边的起始节点u。然后按照v的出边邻接列表中的顺序扫描v的出边，即eo(v)中的边(按出发时间由大到小排列)，若是新满足时间约束的就加入栈s中(例如对于边<v,v’,tv,tv′,w>，满足时间约束表示tv>a(v))。(4)取出栈s中的一条边，判断其是否会对这条边的到达节点造成影响(即这条边的到达时间是否比这条边到达节点的a值小)。如果没有造成影响，则继续取栈s中的边，直到其有影响或栈s为空；如果造成了影响，执行下一步。(5)更新该节点的最早到达时间和其父节点(即a和p值)。然后判断该节点的出边，新满足时间约束则加入栈s。(6)循环步骤(4)、(5)，直到栈s为空，即没有节点的最早到达时间改变。此时，时间最小生成树更新完毕。当δg中包含多条边时，时间最小生成树增量算法只需要按照增加一条边的方法依次判断δg中每一条边更新msta即可，需要说明的是，本发明维护一个变量pos(v)，其表示的是目前在eo(v)中扫描的位置，这样本发明就不会对一条边重复判断。下面本发明给出增量算法中边增加部分的伪代码。可以看到算法1中第1行将δg的边集插入到邻接边列表中，更新图的邻接边列表。第2-3行依次判断改变的δg中的每一条边是否满足时间约束，并且有更小的到达时间，如果是的话再一次判断每条出边对其子孙节点是否造成影响，正如第4-14行。其中第11行判断边是否满足时间约束，第7行判断该边是否有更小的到达时间，如果有，则进行更新，确保了a值只会更新为更小的到达时间。定理1：算法1在时间o(|e∪δe+|)内返回一个更新的msta，其中|e∪δe+|是新时态图的边数。证明：本发明首先证明算法的正确性。当δe+中只有一条边e＝(u,v,tu,tv,w)的时候，如果这条边不满足时间约束，或者这条边满足时间约束但是tv≥a(v)，那么此时v的最早到达时间和他在树中的父节点都不会改变，此时时间最小生成树不变。如果这条边满足时间约束，且tv<a(v)，那么根据算法1中第8行会更新v的最早到达时间a(v)和他的父节点p(v)。a(v)变小之后将其出边中符合时间约束的都入栈(第11-14行)，这些边出栈时可以保证其最早到达时间只有在变得更小时才会更新(第7-8行)，同样也才会对其出边做判断是否入栈，这样可以保证所有的受影响节点都被判断到，也能保证受影响节点的最早到达时间最优变得更小时，树才会更新，最终得到新的msta。对于δg中只含有一条边的情况算法1可以得到更新的msta。当δg中有多条边的时候，本发明同样按照增加一条边的方法，每次处理δg中的一条边，并维护每个点的pos()变量并更新msta。算法1就可以获得更新的msta。下面本发明分析算法1的时间复杂度。首先是更新邻接边列表，也就是算法1的第1行，时间复杂度是o(|e∪δe+|)。对于δg中的每一条边e，如果e满足第3行的条件，算法会扫描v的出边，判断并按同样方法，检查v的子孙节点是否需要更新。最坏的情况就是将时态图中所有的边都扫描一遍。因此算法1的时间复杂度是o(|e∪δe+|)。证毕。part2：删除边的情况这一部分介绍时态图删除边的情况，本发明还是以删除一条边为例开始介绍，下面部分删除的边用e＝(u,v,tu,tv,w)∈δe-表示，本发明先给出引理2。引理2：如果从图g中删除一条边e＝(u,v,tu,tv,w)，那么a(v)的值只会增大或者保持不变。证明：假设删除边e后，a(v)变小了。这就意味着，在时态图中存在一条从根节点到v的路径，它满足时间约束，而且能够比a(v)原来的值还要早到达节点v。那么和定义3中时间最小生成树的定义相矛盾。如果所删除的边e不在初始msta中，那么a(v)将保持不变，因为这条边原先本来就没有被选入到树中。如果所删除的边e在初始msta中，并且时态图中不存在既满足时间约束，到达时间又同为a(v)的边，那么此时a(v)比将变大，如果有满足时间约束，并到达时间同为a(v)的边，那么a(v)将保持不变。证毕。定理2：对于且v≠r，在删除边e＝(u,v,tu,tv,w)，后，如果a(v)变大，那么受影响节点为初始最小生成树中节点v以及v的子孙节点。证明：假设删除边e＝(u,v,tu,tv,w)后a(v)变大，且v有一条出边e′到达节点v′。因为a(v)变大，那么e′的起始时间可能会小于a(v)，此时，<e,e′>将不再满足时间约束，因此需要重新找到一条到达v′且满足时间约束的路径，当重新找到符合要求的路径后，更新v′的最早到达时间和它的父节点。如果a(v′)变大，那么按照同样方法可判断它的孩子节点是否需要更新。因此受影响节点集为最小生成树中的以节点v为根的子树中的所有节点，表示为vs，并将时态图中的不受影响节点集表示为vu，即vu＝g-vs。以下本发明证明vu中的节点的确不受影响。由前面vs和vu的定义可知，路径p(r,x)中一定不包含vs中的节点。所以当删除边e时，路径p(r,x)中的节点不受影响，a(x)和p(x)不会变化，由此可证当删除边e时，受影响节点集是初始最小生成树中节点v以及v的子孙节点。证毕。根据引理2和定理2，可以知道，如果要删除的边e不在初始msta中，那么a(v)和p(v)将不会改变，则msta也将保持不变。如果要删除的边e在初始msta中，那么a(v)和p(v)可能会改变。节点v和它的子孙节点都是受影响节点。因此当删除一条边的时候，从这条边的到达节点开始，不断判断它和它的子孙节点是否要更新，至于更新为何值，只需比较受影响节点的所有入边即可。现在讨论δg中包含多条边的情况。和删除一条边的情况相同，要确定受影响节点，然后对这些节点进行更新即可。下面给出具体步骤：(1)先根据原图g和变化δg更新图的存储结构，要保持每个节点出边按出发时间从大到小的顺序不变。(2)对δg中的所有边进行判断，如果是初始最小生成树(初始msta)中的边，则将该边的到达节点加入集合vs，并将在初始msta中以这些点为根的子树中的点也加入到vs中。(3)对vs中的节点进行初始化，最早到达时间初始化为无穷大，父结点初始化为-1，pos值初始化为1(用pos(v)记录在eo(v)当前扫描的位置)。(4)将满足以下两个条件的边先放入栈s中：(i)这条边的起始节点不在集合vs中，到达节点在集合vs中；(ii)这条边满足时间约束(即这条边的出发时间大于该边起始节点的a值)。(满足这两个条件的边属于vs中节点的入边，其起始节点如果也在vs中则该边一定不满足时间约束，因为vs中节点的a值已经初始化为∞。因此只要选择于vs中节点的入边中满足时间约束的即可)。(5)取出栈s中的一条边，判断其是否会对这条边的到达节点造成影响(即这条边的到达时间是否比到达节点的a值小)。如果没有造成影响，则继续取栈s中的边，直到其有影响或栈s为空；如果造成了影响，执行下一步。(6)根据这条边更新该节点的最早到达时间和其父节点(即a和p值)，a值更新为这条边的到达时间，p值更新为这条边的起始节点。然后判断该节点的出边，满足时间约束则加入栈s。(7)循环步骤(5)和(6)，直到栈s为空，即没有节点的最早到达时间(即a值)改变。此时，时间最小生成树更新完毕。下面给出删除边部分的时间最小生成树增量算法的伪代码。定理3：算法2在时间o(|e-δe-|)内返回一个更新的msta，其中|e-δe-|是新时态图的边数。证明：根据定理2，当删除边e的时候，受影响节点为v和它的子孙节点。本发明找到受影响的节点，然后扫描这些节点的入边以及出边，最后会返回一个更新的msta。算法2遍历受影响节点的入边和出边，最坏的情况就是需要遍历新时态图中所有的边。因此时间复杂度是o(|e-δe-|)，其中|e-δe-|是新时态图的边数。本发明还为删除边的部分提出了一种剪枝策略。在删除初始msta中边e＝(u,v,tu,tv,w)后，本发明可以根据上述增量算法更新msta。假设此时a(v)更新后变大，按照算法2，v和它的所有子孙节点都要加入到受影响节点集中。但是事实上，v的部分子孙节点其实并不会受到影响。比如，v′是v的一个孩子节点，e′是初始msta中从v到v′的时态边。在删除边e后，更新节点v的最早到达时间，得到新的a(v)，但此时a(v)仍不大于e′的出发时间，即此时e′仍满足时间约束，那么v′将不受影响。因此以v′为根的子树不会受到影响，v′以及v′的子孙节点不应该划入到受影响节点集中。通过将节点v′以及其子孙节点从受影响节点集中移除，可以减少算法2所需要扫描的边数，从而加快算法速度。基于以上方法，本发明提出了剪枝策略来减少受影响子图的大小。遍历δg中所有需要删除的边，可以得到目的节点集vd。因为可以知道每个节点在初始的msta中的层数，于是将原受影响节点集vs中的节点按照在初始msta中的层数由大到小进行排序(此时vs为vd中的节点及这些节点的子孙节点)。下面结合图7中的最小生成树给出具体的剪枝步骤，假设删除图7中的v0,v2之间的边和v2，v4之间的边，则vd包含v2和v4。如果从根节点r到节点v的路径p(r,v)上包含节点u，其中u∈vd且u≠v，那么对vs中节点v和它的子孙节点进行标记。因为当从根节点r到节点v的路径p(r,v)上存在其他受影响节点时，那么v就无法直接判定是否受影响。那么图7的树中p(v0,v4)包含节点v2，所以v4无法直接判定是否受影响，标记以v4为根的子树。如果从根节点r到节点v的路径p(r,v)上不包含节点u，其中u∈vd且u≠v，那么当删除以v为目的节点的边时，它的子孙节点可能会不受影响。然后剪枝策略进行下面步骤进一步判断v的子孙节点是否可以被剪枝。那么图2的树中p(v0,v2)不含vd中的节点，所以v2的子孙节点有可能可以剪枝。(1)对v进行标记，即图2中的v2。(2)估算v的新的最早到达时间值，将估算值表示a′(v)。取v-vs中节点到点v的边中到达时间最小的为a′(v)，即a′(v)＝min(tv|(u,v,tu,tv,w),u∈v-vs)。对应于本例即为删除边后的时态图中v0,v1,v3到达v2的最早时间作为估计值。(3)检查v的最到达时间估算值a′(v)是否会对v的未标记的孩子节点造成影响，即判断在初始msta中，v到它的孩子节点的边是否还满足时间约束。如果不满足时间约束，说明会对该孩子节点造成影响，将以该孩子节点为根的子树中的点均标记；如果依然满足时间约束，说明对孩子不造成影响，那么不标记，以这些节点为根的子树可以进行剪枝，那么从vs中剔除这些节点。对应于本例，孩子节点v5未标记，若满足时间约束即可剪枝，否则要进行标记。(4)当依次遍历完vs中所有节点后，vs中剩下被标记的节点就是剪枝后依然受影响的节点。通过以上剪枝方法能够减少受影响节点数，从而减少算法2需要扫描的边数，达到加快速度的目的。实施例2为了使本发明的技术方案更加清楚明白，下面结合实验结果、具体实施以及附图对本发明做进一步说明。实验结果：本发明的实验环境如下：cpu为intel(r)core(tm)i3-6100cpu@3.70ghz，内存为8gb，操作系统为windows1064位，实验所采用的编程语言为c++。本实验使用的数据为slashdot，facebook，hepph，epinions和enron，这些都是真实网络数据。数据集slashdot是从技术网站slashdot收集的的用户交流的网络。数据集facebook是facebook上用户发送给其它用户信息的图。数据集hepph是由高能物理的科学论文作者的合作网络，其中的节点代表作者，边代表两个作者之间的合作出版物。数据集epinions记录了线上产品评级，其中边表示用户之间信任和不信任的链接。数据集enron记录了enron公司员工在1999年到2003年间的电子邮件通信。下表为数据集的简单情况。其中|v|表示节点数，|e|表示边数，deg表示该数据集中节点的最大度数，π表示时态图任意两个节点之间的最大边数，time表示数据集中最大时间间隔。表1数据集dateset|v||e|degπtimeslashdot131k140k36221781590764facebook46k877k2696157137494859hepph28k9193k11134262345306368epinions131k717k3622181590438enron87k1135k3878515661401194717这些数据都是时态图，本发明使用数据中的时间作为起始时间，然后随机增加一个数值作为到达时间。有一些数据是无代价的，本发明将每条边的代价设置为w(e)＝log|di(v)|,其中|di(v)|为边e的到达节点v的入边数量。至于生成树根节点的选取，本发明选择以该节点为根的的生成树中，至少能覆盖数据集中10％节点树的节点为根。本实施例将本发明的增量算法与siluhuang等人在sigmod2015中计算时间最小生成树的方法(对于增量问题，他需要将论文中的算法重新运行一遍)作对比，本发明分别增加、删除1％、5％、10％、15％的边，然后分别运行100次，取平均时间作为最终结果，为了测试本发明算法的有效性，增加的边均是会对最小生成树造成影响的(即增加的边e＝(u,v,tu,tv,w)满足tv<a(v)且tu≥a(u))，删除的边也均是会对最小生成树造成影响的(即删除的边均是初始最小生成树中的边)。本发明用msta+、msta-、msta-pruning分别表示本发明的处理增加、删除和剪枝删除的增量算法，用baseline+和baseline-分别表示用siluhuang等人的算法来解决增加边和删除边的情况。在五个数据集上更新最小生成树的运行时间结果分别如下表所示，能够看到增量算法msta+明显要快于baseline+。因为每次增加边的时候，msta+算法利用已有的初试最小生成树，大大减少了要遍历边的数量，因此能够快速更新msta。增量算法msta-和msta-pruning也明显要快于baseline-。因为算法msta-和msta-pruning比baseline大大减少了要遍历边的数量，而msta-pruning比msta-要更快，说明本发明的剪枝策略是有效的。表2数据集enron(ms)1％5％10％15％baseline+8704.968737.668278.48339.66msta+8.1534.5861.09101.07baseline-8163.128883.927947.377053.3msta-845.512382.443963.114968.66msta-pruning212.11958.552201.623254表3数据集hepph(ms)1％5％10％15％baseline+24682.820033.926069.525194.8msta+921.683041.213137.683114.88baseline-24734.517422.521966.121987.3msta-3257.5713397.619262.727780.9msta-pruning605.214798.1310308.5114596表4数据集facebook(ms)表5数据集slashdot(ms)1％5％10％15％baseline+198.89138.12154.12172.4msta+0.572.202.27.03baseline-214.72143.17143.17185.6msta-21.61103.58103.58218.33msta-pruning8.2147.7647.76143.21表6数据集epinions(ms)1％5％10％15％baseline+875.89845.62862.09870.37msta+0.774.7510.6615.47baseline-868.55663.25761.57814.16msta-51.19303.21571.48698.87msta-pruning27.84161.76356.88478.74实验例1：已知时态图g如图1所示，令节点0为根，g的时间最小生成树如图2所示，图1中的时态图增加边(v0,v1,1,2,1)，增加后新的时态图如图3所示。因为已知时态图g的时间最小生成树，因此知道每个节点的最早到达时间、父节点和扫描到节点出边的位置(即对于节点u的出边(u,v,tu,tv,w)中，tu<a(u)的第一条边的位置)，即已知以下数据：a(v0)＝0p(v0)＝v0pos(v0)＝5a(v1)＝3p(v1)＝v0pos(v1)＝3a(v2)＝5p(v2)＝v0pos(v2)＝3a(v3)＝6p(v3)＝v1pos(v3)＝1a(v4)＝6p(v4)＝v2pos(v4)＝1a(v5)＝8p(v5)＝v2pos(v5)＝1当增加边，首先更新时态图的邻接边列表，依然保持出发时间非递增排序，更新后结果为：v0,<v1,5,6,2><v2,3,6,3><v1,2,3,2><v2,1,5,2><v1,1,2,1>v1,<v4,6,7,1><v3,5,6,1><v3,2,3,2>v2,<v5,6,8,2><v4,5,6,2>v4,<v0,8,9,1>增加的边e＝(v0,v1,1,2,1)满足条件和tv0＝1≥a(v0)＝0，即增加的这条边是满足时间约束的，并且这条边到达节点的到达时间，比初始时间最小生成树中的最早到达时间要小。那么，就把(v0,v1,2)放入到栈s中，开始更新时间最小生成树，如算法1中的第4行。从栈s中取出第一条边，判断它是否具有更小的到达时间，如果有，则更新。此时，取边为(v0,v1,2)，更新节点1的最早到达时间，更新后a(v1)＝2,p(v1)＝1。然后开始检查1的出边，如果有满足时间约束的边，则放入到栈s中。通过检查发现(v1,v3,2,3,2)满足时间约束，因此将(v1,v3,3)放入到栈s中。重复上述过程即可更新时间最小生成树。更新后的时间最小生成树如图4所示。实验例2：已知时态图g如图1所示，令节点v0为根，g的时间最小生成树如图2所示，在如图1所示的时态图中删除边(v0,v2,1,5,2)、(v2,v4,5,6,2)，删除后的新时态图如图5所示。因为和实施例1中时态图相同，所以每个节点的最早到达时间、父节点和扫描到节点出边的位置(即对于节点u的出边(u,v,tu,tv,w)中，tu<a(u)的第一条边的位置)，即已知以下数据：a(v0)＝0p(v0)＝v0pos(v0)＝5a(v1)＝3p(v1)＝v0pos(v1)＝3a(v2)＝5p(v2)＝v0pos(v2)＝3a(v3)＝6p(v3)＝v1pos(v3)＝1a(v4)＝6p(v4)＝v2pos(v4)＝1a(v5)＝8p(v5)＝v2pos(v5)＝1当删除边，首先更新时态图的邻接边列表，依然保持出发时间非递增排序，更新后结果为：v0,<v1,5,6,2><v2,3,6,3><v1,2,3,2>v1,<v4,6,7,1><v3,5,6,1><v3,2,3,2>v2,<v5,6,8,2>v4,<v0,8,9,1>其次，从删除的边集可以得到受影响节点集vs为{v2,v4,v5}。并将这些节点进行初始化：a(v2)＝∞p(v2)＝-1pos(v2)＝1a(v4)＝∞p(v4)＝-1pos(v4)＝1a(v5)＝∞p(v5)＝-1pos(v5)＝1然后在时态图中节点v2,v4,v5的入边中找到满足时间约束的边，放入栈s中。满足时间约束的边有两条(v0,v2,3,6,3)(v1,v4,6,7,1)，于是将(v0,v2,6)(v1,v4,7)放入栈s中。下面进行出栈操作，扫描边。和实验1中出栈部分操作相同。最后得到更新的时间最小生成树，如图6所示。实施例3下面对实施例1的剪枝方法进行说明。删除边的到达节点集d＝{v4,v2}，并将节点按照所在最小生成树的层数由大到小进行排列。根据删除边的到达节点集合，先初始化受影响节点集vs＝{v2,v4,v5}。下面通过剪枝策略进一步减少受影响节点。1、从d中层数最大的节点开始，即v4。如果从根节点v0到v4之间有其他删除节点，即v2。那么以该节点v4为根节点的子树不能剪枝，将节点v4和其子孙节点在vs中标记。vs＝{v2,v4√,v5}2、从d中取下一个节点v2。从根节点v0到这个节点v2之间没有其他的删除节点，那么这个节点的子树可能会剪枝。3、首先将这个节点在vs中进行标记vs＝{v2√,v4√,v5}4、估算节点v2的最小到达时间，从v-vs中的节点{0,1,3}中，找是v2的前驱节点，且到达时间最小的，所以a′(v2)＝min(tv|(u,v2,tu,tv,w),u∈{v0,v1,v3}}，所以取u为0，a′(v2)为6。5、判断a′(v2)对vs中没有标记的孩子是否有影响。v2的孩子有两个v4,v5。节点v4已经被标记，跳过。节点v5未被标记，若a′(v2)对v5不影响，则能剪枝，v5和v5的子孙节点不标记，并从vs中剔除。最终确定的受影响节点为vs＝{v2,v4}。然后继续执行算法2中第5-19行进一步更新时间最小生成树。但是因为减少了受影响节点数，所以剪枝策略能够更快的更新时间最小生成树。显然，本发明的上述实施例仅仅是为清楚地说明本发明所作的举例，而并非是对本发明的实施方式的限定。对于所属领域的普通技术人员来说，在上述说明的基础上还可以做出其它不同形式的变化或变动。这里无需也无法对所有的实施方式予以穷举。凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明权利要求的保护范围之内。当前第1页12