一种应用量子线路计算超图Ramsey数的方法与流程

本发明涉及图的ramsey数领域，特别是一种应用量子线路计算超图ramsey数方法。

背景技术：

量子计算与量子信息的研究对象是用量子力学系统能够完成的信息处理任务，是将量子力学原理和计算机理论结合起来而产生的一门交叉学科。量子计算是一种不同于经典计算的计算方式,具有重大的基础理论作用，并促进高新技术迅猛发展。对于量子计算的研究有助于使得计算进入一种新的境界。

量子计算科学领域令人振奋的结果是,发现了一些量子算法能够比已知经典算法更快地解决问题。目前已知三个这样的量子算法：shor因子分解算法，grover搜索算法和量子仿真算法。其中，grover算法的提出对量子计算的发展起到了重要的作用。进一步的研究表明，量子搜索可以用于加速np复杂类中的问题求解，而np完全问题类一般认为在经典计算机上不可解。

求解ramsey数问题便属于np完全问题，ramsey理论是组合数学的一个重要分支，而图的ramsey数是ramsey理论的一个重要研究方向。然而，到目前为止，只有很少的ramsey数的精确值被确定，已知的上下界大多相距很远，进一步的工作，即使给出较好的上下界，面对的都是非常巨大的计算量。利用经典计算，目前仍没有一种合理的通用方法求出ramsey数的所有值。

许多量子算法设计的本质在于，精心选择函数和最终变换，以便有效地确定有关函数的有用全局信息，而经典计算机上无法快速得到。

技术实现要素：

本发明所要解决的技术问题是现有技术计算ramsey数需要大量计算时间的问题而提供一种应用量子线路计算超图ramsey数的方法。本发明针对给出的r-齐次超图ramsey数的组合优化问题，对该问题进行重新描述，将代价函数映射到搜索问题的布尔函数，进而将求解代价函数转化成求解搜索问题解的个数问题；

本发明为解决上述技术问题采用以下技术方案：

根据本发明所述的一种应用量子线路计算计算超图ramsey数方法，包括以下步骤：

(1)通过r-齐次超图在ramsey数的运算机制中建立量子线路数模；

(2)对量子线路数模中r-齐次超图求解获得ramsey数的最优组合参数；

(3)通过如下公式(2.1)将ramsey数的最优组合参数与量子线路数模中grover算法建立映射关系获得r(m,n；r)的量子线路参数；

其中，给定的正整数n,m,nandr，定义布尔函数fm,n:{0,1}^b(n,r)→{0,1}，当且仅当n≥r(m,n；r)时，fm,n解的个数

(4)通过r(m,n；r)的量子线路参数分别采用量子搜素算法oracle的线路框架、g迭代的线路框架及量子计数的线路框架获得r(m,n；r)的量子线路框架；

(5)通过量子算法对r(m,n；r)的量子线路框架求解获得需要的ramsey的数。

所述步骤(2)中ramsey数的最优组合参数通过如下步骤实现：

2.1从n<r(m,n；r)开始求解上述布尔函数解的个数，则有

2.2每次对n加1，重新进行计算，直到第一次得到则此时的n便为r(m,n；r)。

所述步骤(4)中采用如下步骤分别实现量子搜素算法oracle的线路框架、g迭代的线路框架及量子计数的线路框架构建：

4.1所述oracle的线路框架通过如下公式(1.2)构建可逆的量子算子，

4.2所述g迭代的线路框架通过应用如上所述标记并识别搜索问题的解，使状态空间逐渐向问题解空间收缩；

4.3所述量子计数线路的框架通过对θ的估计满足以下公式(2.3)；

所述步骤(5)中采用如下步骤实现r(m,n；r)的量子算法：

5.1输入给定的m,n和r，r(m,n；r)的已知下界l；

5.2l→n；

5.3对于n，m,n和r，构建并执行上述量子计算线路，确定以的概率得到还是

5.4如果则表明n<r(m,n；r)，将n加1后，执行第(2)步；否则，执行下一步；

5.5n→r(m,n；r)。

有益效果

1、本发明通过设计量子计数线路的具体线路框架，分别对量子搜索算法中的黑箱oracle进行线路设计，对grover迭代进行线路设计，对基于grover迭代和相位估计的量子计数线路进行线路设计，同时，并阐述各个线路框架的运行机制，最后给出了量子计数线路的误差分析；设计应用量子计数线路求解r-齐次超图ramsey数的量子算法，最后，给出了量子计数算法的性能分析。

2、本发明设计的量子算法，对求解r-齐次超图ramsey数具有二次加速作用，即该算法渐近地需要经典算法平方根的运算次数，相对经典算法，在计算性能上有了本质上的提高。尽管，二次加速作用不是特别惊人，但对于计算相对较小的ramsey数，本算法仍然是非常有意义的，比经典算法将有明显的加速。

3、本发明对于计算一些相对较小的ramsey数，将具有非常显著的帮助，例如r(4,6),r(4,5；3)等。由于求解ramsey数属于完全np问题，对于该问题的加速，将对ramsey数求解的研究产生深远意义；与此同时，通过研究量子计算机可有效解决哪类问题及不可有效解决哪类问题，可以对定义量子计算机的复杂类有重要的促进作用，对研究复杂类间的集合和包含关系有重要的影响。

附图说明

图1是应用量子线路计算超图ramsey数方法的流程示意图；

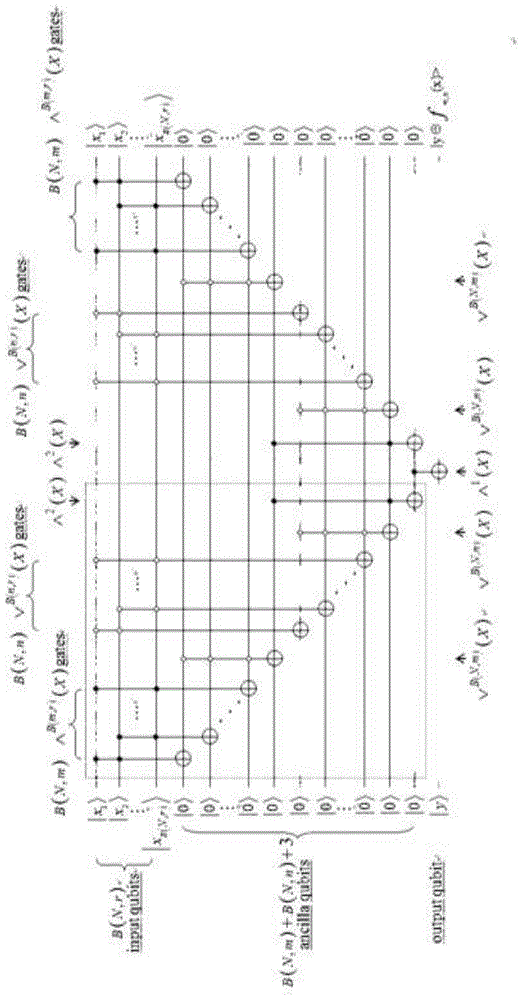
图2是线路框架设计图；

图3是grover迭代gm,n的线路框架设计图；

图4是量子计数的线路框架设计图。

具体实施方式

下面结合附图对本发明的技术方案做进一步的详细说明：

本发明是一种应用量子线路计算超图ramsey数方法，具体流程图如图1，图2是线路框架设计图；图3是grover迭代gm,n的线路框架设计图；图4是量子计数的线路框架设计图。它的实现有如下步骤：

(1)分析r-齐次超图的ramsey数的运算机制，研究r-齐次超图从图表示到代数表示的转化，进而给出求解r-齐次超图的ramsey数的组合优化问题。具体方法如下：

1)r-齐次超图从图表示到代数表示的转化

作为普通图的推广，类似的，对于给定的n和r，可以建立n个顶点的r-齐次超图和二进制串{0,1}^b(n,r)之间的一一对应的关系，其中b定义为二项式系数。为方便起见，定义n个顶点的序列为v≡{1,2,…,n}，定义n个顶点的r齐次超图的集合为和|a|分别定义为a的幂集和基数。对于每一个超图将存在一个唯一的阶矩阵a(g)与之对应，a(g)中的元素为

其中，i1,i2,…,ir∈v，由于图g为无向图，有δ(i1,i2,…,ir)定义为i1,i2,…ir的置换。并且如果|{i1,i2,…ir}|<r，则因此，可以建立如下一一对应的关系gn,r:其满足：

其中，且存在t∈{1,2,…,r}使得当且仅当j<k。称为v的第k个r-相关子集合。对于二进制串x≡x1x2…xb(n,r)∈{0,1}^b(n,r)，当且仅当第k个r-相关子集合在x的对应超图中是一个超边时，xk＝1。

根据上述公式，可以得出

例：如果r＝2，r-齐次超图将退化为普通图，则有

gn,2(g)＝a2,1a3,1…an,1a3,2a4,2…an,2…an,n-1。

对于r＝3，则有：

gn,3(g)＝a3,2,1a4,2,1…an,2,1a4,3,1a5,3,1…an,3,1…an,n-1,1

a4,3,2a5,3,2…an,3,2a5,4,2a6,4,2…an,4,2…an,n-1,2…an,n-1,n-2

2)r-齐次超图的ramsey数r(m,n；r)有如下定义：

对于任意的正整数n,n大于等于r(m,n；r)当且仅当n个顶点的每个r-齐次超图都包含一个m个顶点的完全r-均匀子超图或一个n个顶点的孤立集。

根据该定义，可将求解r-齐次超图的ramsey数问题，映射成如下组合优化问题。

首先，确定超图g中存在m个顶点的完全子超图的个数。对于任意gn,r(g)，从v中选择m个顶点形成子集sα＝{k1,k2,...,km,}，进一步构成如下积形式：

注意到，当且仅当sα中m个顶点构成的图是r-齐次完全超图时，cα＝1。

由于从n个顶点集中选择m个顶点有b(n,m)种情况，则g中包含m个顶点的r-齐次完全子超图的总数量为

类似的，从v中选择n个顶点形成子集tα，可以得到如下公式：

注意到，当且仅当tα中n个顶点构成的图是n个顶点的孤立集时，iα＝1。

由于从n个顶点中选择n个顶点有b(n,n)种情况，则在g中包含n个顶点的孤立集的总数量为

紧接着，定义

hm,n[gn,r(g)]≡cm[gn,r(g)]+in[gn,r(g)]公式(3.7)

注意到，当且仅当g既不包含m个顶点的r-齐次完全子超图也不包含n个顶点的孤立集时，hm,n[gn,r(g)]＝0。

最后，将hm,n[gn,r(g)]设置为组合优化问题的代价函数。对于给定的正整数n,m,n和r，在所有二进制串x∈{0,1}^b(n,r)中，推导出hm,n(x)的全局最小量，设该最小量对应的二进制串为s∈{0,1}^b(n,r)，其对应于n个顶点的超图g*。显然，如果n<r(m,n)，则全局最小量h(s)＝0；当且仅当n≥r(m,n；r)时，hm,n(s)>0。因此，对于给定的m,n和r，取n<r(m,n；r)开始，此时有hm,n(s)＝0；然后每次计算对n加1，直到第一次出现hm,n(s)>0时，此时n＝r(m,n；r)。

3)组合问题重描述，具体方法如下：

对于给定的正整数n,m,nandr，定义布尔函数fm,n:{0,1}^b(n,r)→{0,1}，使其满足

显然，当且仅当n≥r(m,n；r)时，fm,n解的个数

于是，上述组合优化问题可以重新定义如下：

首先，从n<r(m,n；r)开始求解上述布尔函数解的个数，则有

其次，每次对n加1，重新进行计算，直到第一次得到则此时的n便为r(m,n；r)。

因此，计算即解的个数很重要。公式(1.1)所示布尔函数可以看成是对2^b(n,r)个元素的搜索问题。其中，如果x是搜索问题的解，fm,n(x)＝1，否则fm,n(x)＝0。因此，求解ramsey数问题进一步转化为求解对应搜索问题解的个数引入量子搜索算法，搜索问题解的个数的求解可以利用量子计数算法实现，该算法对最好的经典算法有二次加速作用。

(2)求解r(m,n；r)的量子线路框架，具体包括量子搜素算法oracle的线路框架、g迭代的线路框架及量子计数的线路框架。

1)oracle的线路框架设计，实现oracle，需要构建可逆的量子算子，附图2给出了线路框架图。线路的运行机制，具体包括以下步骤：

①定义工作空间，工作空间包括输入输出量子比特，辅助量子比特；

输入量子比特：附图2中前b(n,r)个量子比特，分别代表二进制串x≡x1x2…xb(n,r)∈{0,1}^b(n,r)中的一位，对于任意k∈{1,2,...,b(n,r)}，|xk>代表v中的第k个r-子集，称其为与|xk>相关的r-子集。当n个顶点超图中r-子集包含的顶点存在一条超边连接时，|xk>＝|1>，否则|xk>＝|0>。输入量子比特均初始化为|0>。

输出量子比特：附图2中最后一个量子比特y，用于存储计算结果初始化为|0>。

辅助量子比特：附图2中其余量子比特，提供计算所需的工作空间。辅助量子比特的数量为b(n,m)+b(n,n)+3，均初始化为|0>。

②fm,n(x)的实现，包括如下步骤：

由公式(1.1)可知，求解fm,n(x)必须先求解hm,n(x)。下面逐步求解hm,n(x)，之后求解fm,n(x)并保存fm,n(x)的计算结果，线路构建附图2中红色点框所示。

i.求解超图中m个顶点的r-齐次完全子超图cα

下面公式

可用一个受控非门∧^b(m,r)(x)实现cα。从输入量子比特中选b(m,r)个比特作为受控非门∧^b(m,r)(x)的控制量子比特，选择依据为：如果某量子比特的相关r-子集对应的点集为sα的子集，则其便为∧^b(m,r)(x)的控制量子比特。从前b(n,m)个辅助量子比特中选择一个作为∧^b(m,r)(x)的目标量子比特，用来存储cα的值。当且仅当∧^b(m,r)(x)的控制量子比特为时，目标量子比特才会从|0>翻转到|1>，即n个顶点的超图中存在一个m个顶点的r-齐次完全子超图。

ii.求解超图中m个顶点的r-齐次完全子超图总个数：

下面公式

可用b(n,m)个∧^b(m,r)(x)门和一个v^b(n,m)(x)门确定，∧^b(m,r)(x)的目标量子比特作为v^b(n,m)(x)门的控制比特，即前b(n,m)个辅助量子比特作为v^b(n,m)(x门的控制量子比特。第b(n,m)+1个辅助量子比特作为v^b(n,m)(x)门的目标量子比特。当且仅当v^b(n,m)(x)的控制量子比特为时，目标量子比特的状态从|0>翻转到|1>，所以，当且仅当cm(x)＝0时，v^b(n,m)(x)目标量子比特的状态为|1>。即n个顶点的超图中不存在m个顶点的r-齐次完全子超图。

iii.求解超图中n个顶点的孤立集iα

由公式

可用一个受控非门v^b(n,r)(x)实现iα。从输入量子比特中选b(n,r)个比特作为受控非门v^b(n,r)(x)的控制量子比特，选择依据为：如果某量子比特的相关r-子集对应的点集为tα的子集，则其便为v^b(n,r)(x)的控制量子比特。从第b(n,m)+2至b(n,m)+b(n,n)+1个辅助量子比特中选择一个作为v^b(n,r)(x)的目标量子比特，用来存储iα的值。当且仅当v^b(n,r)(x)的控制量子比特为时，目标量子比特才会从|0>翻转到|1>，即n个顶点的超图中存在一个n个顶点的孤立集。

iv.求解超图中n个顶点的孤立集的总个数

由下面公式

可用b(n,n)个v^b(n,r)(x)门和一个v^b(n,n)(x)门确定，v^b(n,r)(x)的目标量子比特作为v^b(n,n)(x)门的控制比特，即第b(n,m)+2至b(n,m)+b(n,n)+1个辅助量子比特作为v^b(n,n)(x)门的控制量子比特。第b(n,m)+b(n,n)+2个辅助量子比特作为v^b(n,n)(x)门的目标量子比特。由公式(4-4)可知，当且仅当v^b(n,n)(x的控制量子比特为时，目标量子比特的状态从|0>翻转到|1>，所以，当且仅当in(x)＝0时，v^b(n,n)(x)目标量子比特的状态为|1>。即n个顶点的超图中不存在n个顶点的孤立集。

v.求解fm,n(x)

由公式

hm,n[gn,r(g)]≡cm[gn,r(g)]+in[gn,r(g)]公式(3.13)

可知，hm,n(x)＝cm(x)+in(x)，由上文可知，当且仅当cm(x)＝0并且in(x)＝0时，hm,n(x)＝0，此时fm,n(x)＝1，即超图中既不存在m个顶点的r-齐次完全子超图也不存在n个顶点的孤立集；否则fm,n(x)＝0。

可使用一个toffoli门∧²(x)实现上述过程，∧²(x)门的控制量子比特分别为v^b(n,m)(x)门和v^b(n,n)(x)门的目标量子比特，图4-2中最后一个辅助量子比特作为∧²(x)门的目标量子比特。∧²(x)的控制量子比特均为1，即in(x)＝0且cm(x)＝0时，目标量子比特从|0>转换为|1>，否则不变。因此∧²(x)门实现把目标量子比特从|0>转换为|fm,n(x)>。

③将fm,n(x)的结果存储在输出比特中，使用一个标准受控非门∧¹(x)门来计算∧¹(x)的控制量子比特和目标量子比特分别为最后一个辅助量子比特和输出量子比特。

④根据线路fm,n(x)构建即绿色点框中的线路，因此的所有辅助量子比特均变回状态|0>，即是可逆线路。

因此，可以得出，的作用如下：

注意到，输出比特的状态并没有发生变化，为方便起见，的作用可写成如下形式

因此，实现了量子搜索算法中oracle的功能，即可以识别并标记搜索问题的解。

2)接下来设计grover迭代线路框架，附图3给出了grover迭代gm,n的线路框架，包括以下设计：

①输出比特初始化：在输出比特y上先后作用x门和hadamard门，将输出比特状态从|0>转换到

②应用应用如上所述标记并识别搜索问题的解。

③执行条件相移：对输入比特执行条件相移，该线路的作用是2|ψ><ψ|-i，其中|ψ>为均衡叠加态，形式如下

i为单位线性算子^[1]，形式如下

该线路执行grover迭代中第二步至第四步所示操作。

④恢复输出比特：为保证grover迭代的可逆性，在输出比特上先后作用hadamard门和x门,使输出比特恢复至初始状态|0>。

3)然后是量子计数线路的框架设计，附图4给出了量子计数线路的框架设计，包括以下设计：

①基本原理如下，

图4所示线路，主要实现对θ的估计，实现以至少1-ε的成功概率估计θ到m比特精度，其中θ满足以下公式，

因此，通过估计θ，可根据公式(3.18)得到解的个数的一个估计

可证明得，grover迭代可看作是由开始向量和搜索问题组成的均衡叠加态所张成的二维空间的一个旋转。具体地，采用∑x″表示所有x上的搜索问题解的和，∑x′表示所有x上的所有非搜索问题解的和。定义归一化状态

由此，搜索算法的初态可重新表示为

将公式(3.18)代入到公式(3.21)，有

可证明得，一次grover的作用为

即g是|α>和|β>定义的二维空间的一个旋转，旋转角为θ。

进一步，设|a>和|b>是|α>和|β>所张成空间中grover迭代的两个特征向量，可知其相应的特征值为e^iθ和e^i(2π-θ)。因此对grover迭代的算子gm,n应用相位估计线路，可以求解出对θ的一个估计。

②求解过程如下：

如每个相位估计算法，如附图4所示，寄存器1包含个量子比特，寄存器2包含b(n,r)+b(n,m)+b(n,n)+4个量子比特，即的工作空间。寄存器2通过hadamard变换初始化，将初态转换成所有可能输入的均衡叠加态∑x|x>，该状态是本征态(特征向量)|a>和|b>的叠加。

以寄存器1中的的各个量子比特分别作为对寄存器2中比特应用受控grover迭代的控制量子比特，各受控grover迭代的目标量子比特均为寄存器2中的量子比特，grover迭代的次数分别为2⁰,2¹,…,2^t-1。

对寄存器1应用逆fourier变换，并通过在计算基下的测量读出第一寄存器状态，该测量结果便是对θ的一个相当好的估计。

总之，根据相位估计原理，附图4线路在|δθ|≤2^-w精度内，至少以1-ε的概率给出θ或2π-θ的一个估计。进一步，2π-θ和θ在同一精度水平上的估计显然是等价的，因此，实际上，该量子计数算法以1-ε概率在精度2^-w内确定θ，进一步可确定解的个数

③误差分析如下：

利用及对θ的估计，可得到解的个数的一个估计设该估计的误差为

计算表明并且由三角不等式得

代入上式有

将和|δθ|≤2^-w代入公式(3.10)，将得出关于的最终估计，

本文中，选择(注意到，可以取ε→0)，则有因此由附图4知，量子计数算法需要grover迭代的次数为将w及ε代入公式(3.27)得，

特别的，当时，有即该算法必以至少概率给出估计0。反之，估计非0的概率至少是

4)接下来是求解r(m,n；r)的量子计数算法，包括算法描述和性能分析。

①算法描述如下：

求解r(m,n；r)的量子算法

输入：给定的m,n和r，r(m,n；r)的已知下界l^[38]。

输出：r(m,n；r)

过程：

i.l→n。

ii.对于n，m,n和r，构建并执行上述量子计算线路，确定以的概率得到还是

iii.如果则表明n<r(m,n；r)，将n加1后，执行第(2)步；否则，执行下一步。

iv.n→r(m,n；r)

②性能分析如下：

对于给定的n，m,n和r，根据对上节各个线路框架分析，量子计数线路包含个工作量子比特，如果n＝r(m,n；r)，则l[r(m,n；r)]是量子计数线路所需量子比特数的最大值。例如：如果有min(m,n)>r≥3，则对于r-齐次超图最小的ramsey数是r(4,4；3)＝13，应用本算法求解r(4,4；3)＝13将需要1867个量子比特。

上述量子计数线路中需要调用grover迭代次，即调用次oracle，而经典计算机上需要θ(2^b(n,r))次对oracle的调用。因此，在量子计算机上，通过把grover迭代和相位估计技术相结合，能够以比经典计算机要快得多的方式估计出解的数目。该算法能够实现对经典算法的二次加速。

尽管，二次加速作用不是特别惊人，但对于计算相对较小的ramsey数，本算法仍然是非常有意义的。例如，检查r(3,4)＝9的正确性，需要在经典计算机上检查共2^b(9,2)＝2³⁶个包含9个顶点的图，而在量子计算机上，应用本文的算法只需要次grover迭代，比经典算法有明显的加速。

特别的，本算法对于计算一些相对较小的ramsey数，将具有非常显著的帮助，例如r(4,6),r(4,5；3)等。由于求解ramsey数属于完全np问题，对于该问题的加速，将对ramsey数求解的研究产生深远意义。

本发明方案所公开的技术手段不仅限于上述实施方式所公开的技术手段，还包括由以上技术特征任意组合所组成的技术方案。应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也视为本发明的保护范围。