一种考虑运动气动力的尾流下弹性支撑圆柱驰振分析方法与流程

本发明涉及模拟分析技术领域，特别是涉及一种考虑运动气动力的尾流下弹性支撑圆柱驰振分析方法。

背景技术：

输电线尾流驰振的相关研究一般均采用风洞试验和计算流体力学方法。这些方法均不需要明确尾流振动的气动力模型。simpson通过runge-kutta法预测了输电线路的振幅，采用了不考虑气动阻尼的简单近似解析函数对尾流驰振进行了初步的非线性研究。其他采用采用数值模拟研究尾流作用下圆柱由流体诱发振动仍不够充分。

技术实现要素：

本发明的目的在于克服现有技术的不足，提供一种考虑运动气动力的尾流下弹性支撑圆柱驰振分析方法，本方法概念明确，气动力荷载模型简单，能够有效求解下游圆柱的尾流振动。

本发明的目的是这样实现的：

一种考虑运动气动力的尾流下弹性支撑圆柱驰振分析方法，

s1、三分力系数模拟工况

采用计算流体力学软件fluent，分别模拟计算多种t/d工况以及对应的l/d工况下，下游圆柱在尾流中的平均升阻力系数的空间分布，其中，l为圆柱之间沿来流方向的圆心距离，t为圆柱之间垂直于来流方向的圆心距离，d为圆柱直径，得到平均升阻力系数模拟结果：

横流向，多种圆柱间距离和圆柱直径比t/d下的平均阻力系数cd沿着横流向的变化规律；

来流向，多种圆柱间距离和圆柱直径比l/d下的平均阻力系数cd沿着来流向的变化规律；

横流向，多种圆柱间距离和圆柱直径比t/d下的平均升力系数cl沿着横流向的变化规律；

来流向，多种圆柱间距离和圆柱直径比l/d下的平均升力系数cl沿着来流向的变化规律；

s2、升阻力系数拟合分析

采集到一组离散的数据点，采集一组离散的升阻力系数数据点，然后采用matlab多项式进行曲面拟合，拟合出近似的平均阻力系数cd、平均升力系数cl的近似曲面表达式，得到需要的范围空间中任意一点的平均升阻力系数cd、cl的近似值；

s3、尾流驰振运动微分方程建立、求解

对于尾流驰振问题，可以先将上游结构假定为固定不动，将下游结构进行模态分析，分别得到广义质量、广义刚度、广义阻尼和广义力等，这样将一个实际三维结构简化为一种二维的振子计算模型。该模型将上游圆柱假设为固定不动，将下游圆柱简化为一个拥有两个自由度的弹簧振子。以下游圆柱中心为原点，以来流方向为x轴，横风向为y轴，假定下游圆柱的两个自由度分别沿着x轴和y轴两个方向建立质量系数为m，刚度系数分别为kx和ky，结构阻尼系数分别为cx和cy，广义力分别为fx和fy，下游圆柱相对上游圆柱的运动位移分别为x和y的弹簧振子模型，在弹簧振子模型上建立气动力微分方程为：

这里下游圆柱相对于上游圆柱运动的加速度和速度分别为以及。

假设下游圆柱受到的局部相对风速为ur,local，则下游圆柱受到的相对于以局部风速为x轴的局部坐标系的阻力fd和升力fl表示为：

假设下游圆柱受到的局部相对风速为ur,local，则下游圆柱受到的相对于以局部风速为x轴的局部坐标系的阻力fd和升力fl可以表示为：

其中，ρ为空气密度；d为下游圆柱的直径；cd,local为以局部风速ulocal进行无量纲化的平均阻力系数；cl,local为以局部风速ulocal进行无量纲化的平均升力系数。

下游圆柱受到的局部相对风速ur,local可以由局部风速ulocal以及下游圆柱的运动速度表示：

假设整体坐标系与局部坐标系的夹角为θ，则局部坐标系下的fd、fl与整体坐标系下的fx和fy关系为：

同时，假设cd是以来流风速u进行无量纲化的平均阻力系数,cl为以来流风速u进行无量纲化的平均升力系数，则有：

cl,localu²local＝clu²,cd,localu²local＝cdu²(7)

其中夹角θ与局部风速ulocal,局部相对风速ur.local关系为：

将式5、7、8带入式6可得：

同时，来流风速为u，有：

cd,localu²local＝cdu²(10)

令：

得到：

则将式10、式11和式12带入式9可得：

将式13带入式3可得：

式14即为下游圆柱的运动微分方程，根据s2中得到的平均阻力系数cd、平均升力系数cl的表达式，通过直接求解其运动微分方程模拟其运动相关数据。

优选地，s1中，采用流体力学软件fluent,模拟计算了分别为t/d＝0，t/d＝0.5，t/d＝1，t/d＝1.5，t/d＝2对应l./d＝1.5，l./d＝2，l./d＝2.5，l./d＝3，l./d＝3.5，共30个工况，用于计算平均升阻力系数在空间的分布。

优选地，s2中，平均阻力系数cd采用x五次y四次曲面拟合，平均升力系数cl采用x三次y五次曲面拟合。

优选地，s2中，用fluent建模，考虑流固耦合进行两个圆柱在运动状态下的平均升阻力分析，得到的真实的平均升阻力系数cd、cl，对原平均升阻力系数进行差值修正。

优选地，尾流驰振运动微分方程数值求解方法为：

对建立的运动微分方程组采用四阶的runge-kutta法进行数值方法求解，过程如下：

给定的微分方程表示为：

这里t表示时间，将二阶非线性微分方程转换为一阶，令：

其中初值条件为：

又有：

那么方程组可转化为：

然后使用runge-kutta同时求解，对于式23和式25迭代方程为：

对于式24和式26则迭代方程组为：

这里h为时间间隔，可以自行确定。根据迭代方程组式，使用matlab编制迭代程序进行求解。

由于采用了上述技术方案，本发明具有如下有益效果：

本发明首先模拟特定间距比下的下游圆柱的升阻力系数，通过多项式拟合升阻力系数近似的空间分布，获得导线运动的荷载。建立下游导线运动的微分方程。使用四阶runge-kutta法迭代求解下游圆柱运动微分方程。并讨论不同初值条件对下游导线运动收敛的影响，分析初值条件对收敛极限环的影响规律。对比采用流固耦合动网格方法和采用求解运动微分方程模拟的下游圆柱运动参数及气动力荷载的异同。

本发明提出通过不同位置的固定绕流数值模拟，得到特定间距比下的下游圆柱的升阻力系数，通过多项式拟合升阻力系数近似的空间分布，获得导线运动的荷载。获得尾流下的输电导线的平均升阻力系数空间分布，采用包含了气动力高阶项的准定常方法表示了下游导线的气动力，建立尾流驰振理论模型来研究尾流驰振。建立下游导线运动的微分方程。使用四阶runge-kutta法迭代求解下游圆柱运动微分方程。可以有效实现在前方固定圆柱干扰情况下，后端弹性支承的圆柱的气动弹性振动。

对处于尾流作用下，固定的圆柱气动荷载以及弹性支撑的圆柱的气动荷载进行研究，有助于对输电线路中多分裂导线的尾流驰振问题的分析研究。本方法概念明确，气动力荷载模型简单，能够有效求解下游圆柱的尾流振动。

附图说明

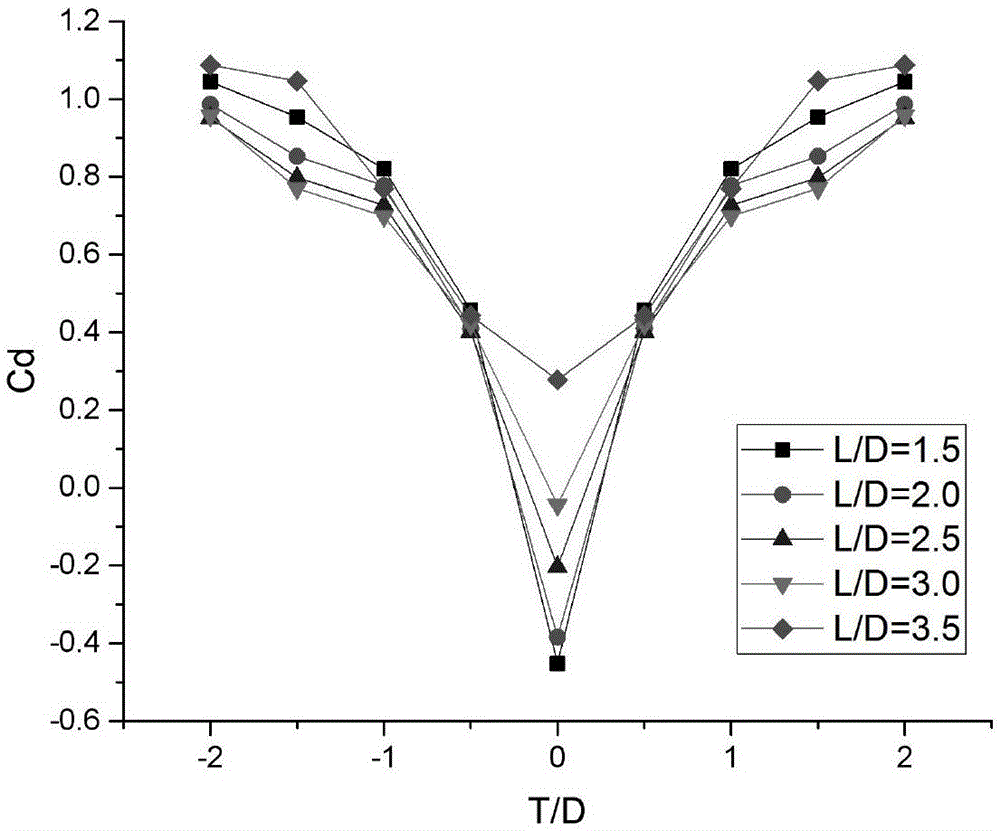
图1为下游圆柱平均阻力系数随t/d变化示意图；

图2为下游圆柱平均阻力系数随l/d变化示意图；

图3为下游圆柱平均升力系数随t/d变化示意图；

图4为平均阻力系数多项式拟合效果示意图；

图5为尾流圆柱质心轨迹对比；

图6为x向位移时程对比；

图7为y向位移时程对比；

图8为x向速度对比；

图9为y向速度对比；

图10为振型分解法示意图；

图11为平均阻力系数修正差随位置变化柱状图；

图12为平均升力系数随位置变化柱状图。

具体实施方式

simpson首先通过runge-kutta法预测了输电线路的振幅，采用了不考虑气动阻尼的简单近似解析函数对尾流驰振进行了初步的非线性研究。上世纪80年代，allnutt等使用线性理论预测存在以一个动平衡位置为中心的极限环，并将极限环用正弦函数来表达。之后，price通过风洞试验获得尾流下的输电导线的平均升阻力系数空间分布，采用包含了气动力高阶项的准定常方法表示了下游导线的气动力，建立尾流驰振理论模型来研究尾流驰振。

本发明将首先模拟特定间距比下，下游圆柱的升阻力系数，通过多项式拟合升阻力系数近似的空间分布，获得导线运动的荷载。建立下游导线运动的微分方程。使用四阶runge-kutta法迭代求解下游圆柱运动微分方程。并讨论不同初值条件对下游导线运动收敛的影响，分析初值条件对收敛极限环的影响规律。对比采用流固耦合动网格方法和采用求解运动微分方程模拟的下游圆柱运动参数及气动力荷载的异同。

一种考虑运动气动力的尾流下弹性支撑圆柱驰振分析方法，包括：

计算工况

圆柱的直径为30mm。取相对风速vr为50，即来流风速u为14m/s。流体入口采用入口边界(velocity-inlet)，来流速度设置为14m/s，湍流强度设置为5％；出口采用压力出口(pressure-outlet)；上下壁面设置为对称边界条件(symmetry)；湍流模型选择sstk-ω模型；时间步设置为0.0004s。

如图10所示，基于振型分解法分别取横向和竖向振型，可将多自由度的三维模型转化为两自由度的二维模型。默认圆柱二维模型的长度为1。为了获取三分力系数(升阻力系数)的表达式，分别模拟计算了分别为t/d＝0，t/d＝0.5，t/d＝1，t/d＝1.5，t/d＝2对应l./d＝1.5，l./d＝2，l./d＝2.5，l./d＝3，l./d＝3.5等30个工况计算三分力系数在空间的分布，从而拟合出对应的三分力系数表达式，其中，l为圆柱之间沿来流方向的圆心距离，t为圆柱之间垂直于来流方向的圆心距离，d为圆柱直径，两个圆柱之圆心连线与来流风向(x轴)形成的夹角为α。

表1主要参数

升阻力系数模拟结果

图1给出了下游圆柱在尾流中在横流向(y方向)圆柱间距离和圆柱直径比t/d从-2变化到2，变化步长0.5，共36个截面下的平均阻力系数cd沿着横流向的变化规律(设后方圆柱位于前方圆柱下方时，t为负；后方圆柱位于前方圆柱上方时，t为正)。从图1中可以看出，尾流圆柱的平均阻力系数在x轴上具有对称性，越接近x轴平均阻力系数越小，在t/d＝0的时候阻力系数达到最小值。在t/d＝0时，l/d＝1.5、l/d＝2.0、l/d＝2.5、l/d＝3.0这四种间距工况，由于下游圆柱离上游圆柱距离较近，下游圆柱的平均阻力系数值为负，在力上表现为吸力。在-1≤t/d≤0以及0≤t/d≤1范围内，下游圆柱平均阻流系数随着t/d的增大(或减小)变化较快，说明这个距离上，下游圆柱受到上游圆柱的尾流影响较大。

图2给出了下游圆柱在尾流中来流向(x方向)圆柱间距离和圆柱直径比l/d从1.5变化到3.5，变化步长0.5，共25个截面下的平均阻力系数cd沿着来流向的变化规律。从图2中，可以看出在1.5≤l/d≤3.0范围内，t/d＝0.5、t/d＝1.0、t/d＝1.5、t/d＝2.0这四种工况下游圆柱的平均阻力系数随着l/d的增加而小幅度降低。而同样在1.5≤l/d≤3.0范围内，t/d＝0工况下，下游圆柱的平均阻力系数随着l/d的增加而大幅度的增加，同时都为负数。说明在t/d＝0这种下游圆柱正对上游圆柱这种工况中，下游圆柱受到的是的是类似一种上游圆柱的吸力。在3.0≤l/d≤3.5范围内，所有工况下游圆柱的平均阻力系数均有上升，说明下游圆柱离上游圆柱距离变大之后，下游圆柱受上游圆柱的影响变小。

图3给出了下游圆柱在尾流中在横流向(y方向)圆柱间距离和圆柱直径比t/d从0变化到2.0，变化步长0.5，共25个截面下的平均升力系数cl沿着横流向的变化规律。从图3中可以看出，在t/d＝0.5的时候,所有l/d的情况升力系数达到最小值，并都为负数，变现为向y轴负方向的力。从工况t/d＝0到工况t/d＝0.5，所有l/d的情况下，升力系数都是呈现下降的趋势，说明在t/d＝0.5这种间距下，上游圆柱的尾流对下游圆柱的影响较大。在0.5≤t/d≤1范围内，所有l/d的工况下的升力系数都表现为上升，说明在此范围内，上游圆柱对下游圆柱升力系数的影响慢慢地减少，下游圆柱的升力系数逐渐像单圆柱下的升力系数靠近，即升力系数逐渐向0靠近。

升阻力系数拟合分析

曲面拟合是一种非常常用的技术手段，在工程、实验、统计、和计算机图形方面都有着非常广泛的应用。在应用中。我们通过测量或其他手段采集到一组离散的数据点，然后采用多项式进行拟合，拟合通常采取插值和逼近两种方式。通过插值方式得到的方程，所有离散的数据点都会在这个拟合得到的方程所表示的曲面之上，但是因为误差需求，要求我们需要的数据范围接近我们离散点的数据范围。通过逼近方式得到的方程。并不会要求所有的离散数据点都在拟合方程所表示的曲面之上，只要在可接受范围内，方程表示的曲面接近这些离散数据点即可，如图4所示意。

本发明在模拟获得的平均气动力系数cd、cl的基础上，使用matlab多项式拟合出近似的平均气动力系数cd、cl的近似曲面表达式。考虑到曲面拟合整体广顺性要求，平均阻力系数cd采用x五次y四次曲面拟合，平均升力系数cl采用x三次y五次曲面拟合。多次拟合的表达式如式1和2所示，系数见表2平均阻力系数多项式拟合系数、表2平均升力系数多项式拟合系数。

表2平均阻力系数多项式拟合系数

表3平均升力系数多项式拟合系数

根据式1和式2以及其系数表、表3中的平均气动力系数cd、cl的近似拟合的多项式，我们可以得到需要的范围空间中任意一点的平均升阻力系数cd、cl的近似值。

进一步地，用fluent建模，考虑流固耦合进行两个圆柱在运动状态下的平均升阻力分析，得到的真实的平均升阻力系数cd、cl，对原平均升阻力系数进行差值修正。典型的平均升阻力系数差值δcd、δcl修正图形如图11、图12所示。

尾流驰振运动微分方程建立

建立运动微分方程时，将上游圆柱假设为固定不动，将下游圆柱简化为一个拥有两个自由度的弹簧振子。以下游圆柱中心为原点，以来流方向即顺风向为x轴，垂直于来流方向即横风向为y轴。假定下游圆柱的两个自由度分别沿着x轴和y轴两个方向建立刚度系数分别为kx和ky、阻尼系数分别为cx和cy、位移分别为x和y的弹簧振子模型。所以在此运动力学模型上可以建立气动力微分方程为：

假设下游圆柱受到的局部相对风速为ur,local，则下游圆柱受到的相对于以局部风速为x轴的局部坐标系的阻力fd和升力fl可以表示为：

其中，ρ为空气密度；d为下游圆柱的直径；cd,local为以局部风速ulocal进行无量纲化的平均阻力系数；cl,local为以局部风速ulocal进行无量纲化的平均升力系数。

下游圆柱受到的局部相对风速ur,local可以由局部风速ulocal以及下游圆柱的运动速度表示：

假设整体坐标系与局部坐标系的夹角为θ，则局部坐标系下的fd、fl与整体坐标系下的fx和fy关系为：

同时，假设cd是以来流风速u进行无量纲化的平均阻力系数,cl为以来流风速u进行无量纲化的平均升力系数，则有：

cl,localu²local＝clu²,cd,localu²local＝cdu²(7)

其中夹角θ与局部风速ulocal,局部相对风速ur.local关系为：

将式5、7、8带入式6可得：

同时，来流风速为u，有：

cd,localu²local＝cdu²(10)

令：

可得：

则将式10、式11和式12带入式9可得：

将式13带入式3可得：

式14即为下游圆柱的运动微分方程。可以看出，下游圆柱的气动荷载不仅仅与其运动速度有关，同时还与其所处的位置有关的cd、cl系数有关。在上一节中，我们已经获得了升阻力系数cd、cl在空间中近似的分布函数。则我们可以通过直接求解其运动微分方程模拟其运动相关数据。

尾流驰振运动微分方程数值求解

本文对建立的运动微分方程组将采用四阶的runge-kutta法进行数值方法求解。runge-kutta法是由卡尔龙格和马丁威尔海姆库塔提出的用于非线性常微分方程解的迭代方法。四阶runge-kutta法是十分常用的高精度单步算法，在已知方程的导数和初值信息时可以非常方便的利用计算机进行编程求解。

基本过程如下，当初值为：

y′＝f(t,y),y(t0)＝y0(15)

而有：

这样，yn+1的值等于由现在的值加上估算斜率和时间间隔h的乘积。在四阶中，估算的斜率为：

则该问题的下一个值为：

上述公式的局部截断误差为o(h⁵)。

尾流下部圆柱的失稳通常表现为具有良好光滑性质的极限环运动。因为runge-kutta法推导基于泰勒展开式，对于这类拥有光滑性质的方程具有很好的精度。计算yn+1时只需要知道前面的yn的计算结果，可以编程实现自动迭代计算。同时，时间间隔h可以由我们人为进行选择，可以选择在不同情况下选择最优的时间间隔进行计算。对于本文问题，给定的微分方程可以表示为：

方程为二阶非线性微分方程组，则我们需要将二阶非线性微分方程转换为一阶。我们令：

其中初值条件为：

又有：

那么方程组可转化为：

即将原来的二元二阶方程组转化为了四个独立的一阶微分方程，然后使用runge-kutta同时求解。对于式27和式29迭代方程为：

对于式28和式30则迭代方程组为：

根据迭代方程组式，使用matlab编制runge-kutta迭代程序进行求解。

分析结果和数值结果的对比分析

在双圆柱绕流问题的研究中，准定常方法是常用的研究尾流失稳的方法。而使用flunet动网格来模拟尾流失稳问题也是个相对可靠的方法。对于特定的尾流失稳问题，采用准定常方法和采用fluent动网格方法求解的结果比较接近。但对于在准定常方法求解下游圆柱运动方程时采用的荷载模型与，本节将比较准定常方法和flunet动网格模拟的结果中气动荷载的异同。

极限环运动参数对比

如图5-图9所示，流固耦合方法和采用求解动力学方程方法的最终收敛的极限环的x和y方向的位移时程曲线幅值和频率接近，x方向和y方向的速度时程曲线也同样相似，除了在极限环远端其x、y的位移有一点差异，其他位置都吻合较好，可能是由于在远端处，拟合生阻力系数时处于拟合数据点的边缘，拟合数据有一定的误差所导致的。

最后说明的是，以上优选实施例仅用以说明本发明的技术方案而非限制，尽管通过上述优选实施例已经对本发明进行了详细的描述，但本领域技术人员应当理解，可以在形式上和细节上对其作出各种各样的改变，而不偏离本发明权利要求书所限定的范围。