一种面向超材料的等几何拓扑优化方法与流程
本发明属于材料结构优化领域,更具体地,涉及一种面向超材料的等几何拓扑优化方法。
背景技术:
近几年来,超材料作为新材料技术的重要组成部分,所表现出的超常物理特性受到了广泛的关注。在声、光、热、力、电磁学领域特殊性能,使其在工业、军事等领域具有十分广阔的应用前景,人们通过设计材料微结构,可以人工调控原有材料的机械属性,从而获得自然界中不存在的机械属性。
拉胀超材料通常表现出轻质、高阻尼、吸声、隔热等物理特性,在功能材料中扮演重要角色,对航空航天、半导体器件、光学元件、精密仪器以及建筑材料等领域的发展具有重大意义,作为拉胀超材料的核心,超材料内的微结构将对整体性能起着至关重要的作用。
拓扑优化作为结构优化方法之一,对微结构设计有着特有的优势,由于设计目标越来越具有多样化、复杂化等特点,因此对优化的精度和效率等方面都有了更高的要求,而目前在材料微结构设计过程中常用的有限元方法在进行细化网格划分时,会产生大量的单元,使过程更加繁琐、耗时,因此,有限元分析法在拓扑优化设计中的网格依赖问题较突出,以致于对优化结果产生棋盘格问题、非平滑的“zig-zag”边界以及局部极小值等问题,从而严重影响微结构的优化设计,以及所获得的超材料性能。
技术实现要素:
针对现有技术的以上缺陷或改进需求,本发明提供了一种面向超材料的等几何拓扑优化方法,通过采用基于nurbs函数的方法构建材料密度的优化设计模型,其基于等几何分析,确保nurbs曲面的cad模型与cae模型一致,避免在在材料微结构设计过程中采用有限元方法进行细化网格划分,简化计算,降低计算复杂度,缩短计算时间,快速高效的实现多孔材料单胞结构向拉胀超材料的转化,计算精度高。
为实现上述目的,按照本发明,提供了一种面向拉胀超材料的等几何拓扑优化方法,其特征在于,该方法包括下列步骤:
(a)选取多孔材料的单胞结构作为待优化对象,其中,多孔材料作为宏观材料,单胞结构作为微结构,选择与该微结构相应的nurbs基函数和控制顶点,以此构建与待优化微结构设计域对应的nurbs曲面;
(b)通过渐进均匀化方法等效材料属性,以此获得多孔材料的弹性张量矩阵,根据该弹性张量矩阵建立微结构密度的优化设计模型,使得微结构在体积减小的同时具有负泊松比,即使宏观材料具有拉胀超材料属性;
(c)建立微结构密度的优化准则,根据该优化准则计算优化模型,直至获得收敛的密度值,以此获得优化后的微结构的密度值,从而实现多孔材料的微结构的拓扑优化。
进一步优选地,在步骤(b)中,密度的优化设计模型优选按照下列表达式进行:
其中,ρi,j是点(i,j)处的密度,(i,j)是微结构设计域上点的坐标,n,m分别是在构建nurbs曲面的过程中建立的两个参数方向上的控制顶点的总数量,ω是微结构即设计域,u是设计域上的位移场,
进一步优选地,多孔材料的弹性张量矩阵dh优选按照下列表达式进行:
其中,|ω|是微结构的面积,d是弹性张量,ε(u0)是线性独立的单元测试应变场,ε(u)是微结构内的应变场。
进一步优选地,ε(u)是按照下列表达式计算获得:
其中,u是设计域上的位移场,v是微结构可允许的位移场空间hper,
进一步优选地,高斯积分点处的密度
其中,
进一步优选地,光滑后的控制顶点密度
其中,ρi,j是控制顶点(i,j)处的密度,w(ρi,j)是控制顶点(i,j)处的权重,
进一步优选地,双变量nurbs基函数
其中,ni,p(ξ)是在参数方向上定义的一个b样条基函数,是第i个p次基函数,n是ni,p(ξ)中基函数的个数,p为基函数的次数,由节点向量ξ={ξ1,ξ2,…,ξn+p+1}构成;mj,q(η)是在另一个参数方向上定义的b样条基函数,表示第j个q次基函数,m代表mj,q(η)中基函数的个数,q为基函数的次数,由节点向量
进一步优选地,在步骤(c)中,优化准则优选按照下列表达式进行:
其中,
总体而言,通过本发明所构思的以上技术方案与现有技术相比,能够取得下列有益效果:
1、本发明提供的方法基于nurbs函数构建材料密度函数,有效避免对微结构设计过程中常见的棋盘格问题、网格依赖问题等数值不稳定问题,从而确保面向拉胀超材料结构优化设计方法的有效性;
2、本发明提供的方法基于等几何分析,确保nurbs曲面的cad模型与cae模型一致,对采用传统有限元方法产生的误差能够有效解决,提高了计算精度和求解效率;
3、本发明提供的方法快速高效地实现从多孔材料的单胞结构向拉胀超材料的转化,计算简单,精度高,适用于面向材料微结构优化设计问题研究,如寻找刚度最优材料微结构以及后续多相负泊松比结构优化设计问题,等等。
附图说明
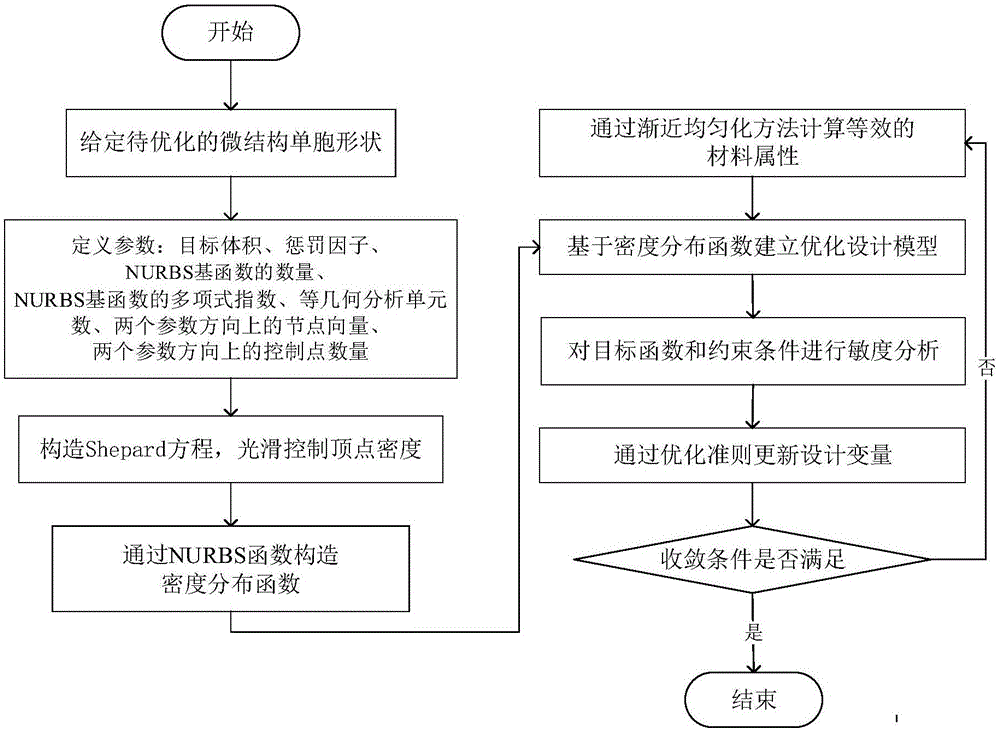
图1是按照本发明的优选实施例所构建的面向超材料的等几何拓扑优化方法流程图;
图2是按照本发明的优选实施例中待优化的微结构初始设计示意图;
图3按照本发明的优选实施例中的结构优化后得到的结微构示意图;
图4按照本发明的优选实施例中的微结构优化过程的收敛结果示意图。
具体实施方式
为了使本发明的目的、技术方案及优点更加清楚明白,以下结合附图及实施例,对本发明进行进一步详细说明。应当理解,此处所描述的具体实施例仅仅用以解释本发明,并不用于限定本发明。此外,下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。
图1是按照本发明的优选实施例所构建的等几何材料密度场结构拓扑优化方法流程图,如图1所示,具体流程如下:
(1)给定待优化多孔材料的单胞结构作为设计域,其中,多孔材料作为宏观材料,单胞结构作为微结构;
(2)定义参数:定义nurbs基函数的多项式指数、nurbs基函数的数量、等几何分析单元、两个参数方向上的节点向量,两个参数方向上的控制点数量为,根据上述参数确定nurbs基函数和控制顶点,并以此建立与设计域对应的nurbs曲面;接着设定设计域的目标体积和惩罚因子;两个节点向量的方向即为参数方向ξ,η。
(3)用shepard函数光滑控制顶点密度,光滑后的控制顶点密度可表示为:
式中,
(4)通过nurbs函数构造密度分布函数:
其中,(ξ,η)为参数坐标,
ni,p(ξ)是在参数方向上定义的一个b样条基函数,表示第i个p次基函数,n代表ni,p(ξ)中基函数的个数,p为基函数的次数,由节点向量ξ={ξ1,ξ2,…,ξn+p+1}构成;mj,q(η)是在另一个参数方向上定义的b样条基函数,表示第j个q次基函数,m代表mj,q(η)中基函数的个数,q为基函数的次数,由节点向量
(5)通过渐近均匀化方法等效材料属性:
|ω|代表微结构的面积,d是弹性张量,
υ表示微结构可允许的位移场空间hper。
(6)基于密度分布函数构建结构优化设计模型:
其中,ρi,j是点(i,j)处的密度,(i,j)是待优化微结构设计域上点的坐标,n,m分别是在构建nurbs曲面的过程中建立的两个参数方向上的控制顶点的总数量,ω是微结构设计域,u中设计域上的位移场,
具体地,平衡方程是通过虚功原理建立的,定义为:
a是双线性能量函数,l是线性载荷函数。u是在结构设计域ω的位移场,δu是在sobolev空间h1(ω)的虚位移场。d表示弹性张量矩阵。
(7)对目标函数和约束条件进行敏度分析求解,即目标函数和约束条件分别对设计变量进行求导,求导公式如下:
(8)通过优化准则更新设计变量,得到更新后的密度值。优化准则表达形式为:
其中,
(9)判断收敛条件是否满足:若满足,则输出当前设计结果作为最优结构,否则,返回步骤(5)继续进行优化,直到满足条件。
收敛条件定义为:
其中,
下面结合图2~4所示的一个具体实施例来对本发明的上述步骤进行详细说明:
如图2所示:
(1)待优化微结构设计域为1×1的正方形,
(2)定义参数如下:nurbs基函数的多项式指数为2、nurbs基函数的数量为102*102、等几何分析单元数100*100、两个参数方向上的节点向量ξ={0,0,0,0.01,…,0.99,1,1,1}、
(3)用shepard函数光滑控制顶点密度,光滑后的控制顶点密度可表示为:
式中,
(4)通过nurbs函数构造密度分布函数:
其中,(ξ,η)为参数坐标,
ni,p(ξ)是在参数方向上定义的一个b样条基函数,表示第i个p次基函数,n代表ni,p(ξ)中基函数的个数,p为基函数的次数,由节点向量ξ={ξ1,ξ2,…,ξn+p+1}构成;mj,q(η)是在另一个参数方向上定义的b样条基函数,表示第j个q次基函数,m代表mj,q(η)中基函数的个数,q为基函数的次数,由节点向量
(5)通过渐近均匀化方法等效材料属性:
|ω|代表微结构的面积,d是弹性张量,
v表示微结构可允许的位移场空间hper。
(6)基于密度分布函数构建结构优化设计模型:
其中,ρi,j是点(i,j)处的密度,(i,j)是待优化微结构设计域上点的坐标,n,m分别是在构建nurbs曲面的过程中建立的两个参数方向上的控制顶点的总数量,ω是微结构设计域,u中设计域上的位移场,
具体地,平衡方程是通过虚功原理建立的,定义为:
a是双线性能量函数,l是线性载荷函数。u是在结构设计域ω的位移场,δu是在sobolev空间h1(ω)的虚位移场。d表示弹性张量矩阵。
(7)对目标函数和约束条件进行敏度分析求解,即目标函数和约束条件分别对设计变量进行求导,求导公式如下:
(8)通过优化准则更新设计变量,得到更新后的密度值。优化准则表达形式为:
其中,
(9)判断收敛条件是否满足:若满足,则输出当前设计结果作为最优结构,否则,返回步骤(5)继续进行优化,直到满足条件。
收敛条件定义为:
其中,
优化后的微结构如图3所示。其优化过程可简述为,通过构造shepard方程,光滑控制点密度,用以构造密度分布函数,通过渐近均匀化方法等效材料属性,进而对单元刚度矩阵进行求解,以构造密度分布函数构建的结构优化设计模型。通过优化设计模型,对目标函数和约束条件进行灵敏度分析,得到设计变量,再通过优化准则对设计变量进行更新,得到优化的结构,进而判断是否满足收敛条件,即相邻两次迭代的设计变量的最大变化值小于0.01,若满足则输出优化结构,若不满足,则返回步骤求解单元刚度矩阵,继续进行优化,直到满足收敛条件,输出最优结果。
图4为目标函数的迭代曲线,从曲线可以看出,初始时由于体积分数未达到约束时,目标函数有波动。当体积分数达到约束值,目标函数开始稳定变化,逐渐收敛,在迭代37次后完成优化。表明了该设计方法能够快速的收敛并达到稳定值,且最终的结构边界光滑,效果显著。
本领域的技术人员容易理解,以上仅为本发明的较佳实施例而已,并不用以限制本发明,凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等,均应包含在本发明的保护范围之内。
- 还没有人留言评论。精彩留言会获得点赞!