基于自学习权重的多视图投影聚类方法与流程

本发明属机器学习技术领域，具体涉及基于自学习权重的多视图投影聚类方法。

背景技术：

聚类问题属于机器学习和数据挖掘领域重点研究的基础问题之一，其目的是将具有相似特征的数据点聚到同一类。在过去的几十年中，已经提出了许多聚类方法，例如k均值聚类，谱聚类，谱嵌入聚类，多视图聚类等。目前，随着数据采集设备的发展和新采集手段的出现，获得了大量产生于不同的数据源或特征子集的数据，其中每一个数据源或特征子集构成一个视图。例如，在网络文本数据中，不同的文档可以用不同的语言编写；在生物学数据中，可以使用不同的技术来测量不同的基因；在视觉数据中，可以使用不同的视觉特征来呈现每个图像或视频，这样就形成了多视图数据。多视图学习则是处理这类数据的有效手段。

多视图聚类算法主要有三类：基于张量的方法、基于子空间的方法和基于图的多视图聚类方法。其中，基于图的多视图聚类方法较另外两种方法通常能够取得更好的效果。大多数传统的基于图的多视图聚类方法包含两个步骤：首先根据一定的构图方法为每一个视图的特征构建一个相似度矩阵，其次运用权重或罚项来整合这些相似度矩阵得到指示向量，最后，以这些指示向量为输入，利用k均值方法进行聚类。

为有效整合多视图的优势，xia等人在文献“multiviewspectralembedding[j].ieeetransactionsonsystemsman&cyberneticspartb,2010,40(6):1438-1446.”以及karasuyama等人在文献“multiplegraphlabelpropagationbysparseintegration[j].ieeetransactionsonneuralnetworksandlearningsystems,2013,24(12):1999-2012.”分别提出了一种自适应权重学习策略，并广泛应用到了多视图学习中。以上所提到的这两种方法明确定义了每个视图的权重，并将其看成一组变量去优化。然而，由于这些方法同时需要引入正则化参数来避免平凡解的产生，而最终聚类的结果对正则化参数较为敏感，使得该参数难以调节。因此，传统的权重学习策略不实用。同时，传统方法直接将原始的高维数据用于聚类任务的输入，而忽略了高维数据中包含的噪声和冗余信息，这可能导致学习性能的下降以及计算复杂性的增加。为了解决这个问题，最直接的方法应该是首先对原始的高维数据进行降维，然后对投影后的低维数据进行聚类。

另外，虽然基于图的方法较能取得较好的聚类结果，但由于图的构造和聚类任务的分离，它主要有两个缺点：(1)算法最终的聚类结果取决于初始输入相似度矩阵的质量，不可靠的相似度矩阵会导致不好的聚类结果。(2)最终的聚类结果还依赖于k均值聚类或其他离散化程序。可以认为，如果将相似度矩阵看成一个变量并使其能直接揭示数据集的聚类结构，聚类的性能将得到极大的改善。在结构化图学习的启发下，可以将相似度矩阵看作一变量，并通过秩约束去优化。也就是说，可以通过获得的相似度矩阵来得到数据的聚类结构，而不需要再采用其他离散化程序进行聚类任务。此外，本发明提出了两种无参数的权重学习策略，构造了两种目标函数，有效地整合不同视图的有效信息，通过交替进行结构图优化和子空间学习，以在低维空间中聚类原始的高维数据。

技术实现要素：

要解决的技术问题

为了避免现有技术的不足之处，本发明提出一种基于自学习权重的多视图投影聚类方法。

技术方案

一种基于自学习权重的多视角投影聚类方法，其特征在于步骤如下：

步骤1：投影结构图学习

令x＝[x1，…，xn]t∈rn×d表示数据矩阵，其中n是数据点的数量，d是特征的维数，每个数据点属于c类中的一类；给定数据矩阵x，每个数据点xi表示为亲和图上的顶点，并且每个边表示一对顶点的相似关系；xi和xj之间的边的权重定义为sij，表示相似度矩阵；结构图学习模型首先将相似度矩阵s定义为变量，并且可以通过解决以下问题来优化：

其中μ是正则化参数，1表示所有元素都是一的列向量；对于每个数据点xi，所有数据点{x1，x2，…，xn}都以sij大小的概率可以作为xi的近邻；

在上式的基础上添加秩约束：

将上式进一步扩展到以下问题：

其中表示投影矩阵，m是投影维度；st＝x^tx表示总散度矩阵，增加约束w^tstw＝i表示投影后的子空间上的数据统计不相关；

步骤2：建立自学习权重的多视图投影聚类框架

对于多视图数据，令x1，x2，…，xv分别表示每个视图的数据矩阵，v为视图数，其中为和v＝1，…，v，dv为第v个视图的特征维度；

为有效利用不同视图的信息，需要对不同视图赋予一定的权重βv(v＝1，…，v)，这样步骤1的求解问题可变为：

由于权重βv并不是人为事先给定的，而是需要通过构造目标函数去求解得到，上式的结果为一个平凡解，即只有最有效的视图对应的权重有值，其它视图对应的权重为零，因此必须通过对权重βv进行合理的约束；于是本发明采用了两种权重自学习的方法去求得不同视图所对应的权重，以有效整合不同视图的有效信息；

利用合适的因子权重与不同视图相结合，有这样步骤1的求解问题可变为：

其中α＝[α1，α2，…，αv]^t，表示投影矩阵，mv为第v个视图的投影维度；

步骤3：采用dwmpc算法求解

令σi(ls)是ls的第i个最小特征值；很容易看出σi(ls)≥0，因为ls是正半无限的；因此，对于足够大的λ值，问题(4)，相当于：

其中λ取值足够大以确保矩阵ls前c个最小的特征值为零，于是矩阵ls的秩为n-c，根据樊畿理论可知：

于是，问题可以转化为求解：

可以通过一个迭代优化算法求解上式；

1、固定αv与s，求解wv和f；由于变量wv和f相互独立，其取值可分别由以下两式求得：

公式可改写为：

由于上式对于不同的v是相互独立的，可通过下式单独求解每一视图对应的wv：

上式wv的最优解是由前mv个最小特征值所对应的特征向量所组成；公式(9)中f的最优解是由ls前c个最小特征值所对应的特征向量所组成；

2、固定αv、wv和f，求解s；公式(7)的第一项可简化表示为其中然后问题(7)变为：

在谱分析中，有一个重要而基础的公式：

利用上式，对于每一向量si，公式(12)可表示为：

其中表示矩阵s的第i行，

公式(14)可简化表示为：

其中是以第j个元素为的列向量；该公式可以得到闭式解；

3、固定wv和s，求解αv；令公式(7)可表示为：

其对应的拉格朗日函数为：

其中λα为拉格朗日乘子；通过简单的代数变换

通过以上三个步骤，交替迭代更新wv、f、s和αv，不断重复该步骤直至目标函数收敛。

一种基于自学习权重的多视角投影聚类方法，其特征在于步骤如下：

步骤1：投影结构图学习

令x＝[x1，…，xn]^t∈r^n×d表示数据矩阵，其中n是数据点的数量，d是特征的维数，每个数据点属于c类中的一类；给定数据矩阵x，每个数据点xi表示为亲和图上的顶点，并且每个边表示一对顶点的相似关系；xi和xj之间的边的权重定义为sij，表示相似度矩阵；结构图学习模型首先将相似度矩阵s定义为变量，并且可以通过解决以下问题来优化：

其中μ是正则化参数，1表示所有元素都是一的列向量；对于每个数据点xi，所有数据点{x1，x2，…，xn}都以sij大小的概率可以作为xi的近邻；

在上式的基础上添加秩约束：

将上式进一步扩展到以下问题：

其中表示投影矩阵，m是投影维度；st＝x^tx表示总散度矩阵，增加约束w^tstw＝i表示投影后的子空间上的数据统计不相关；

步骤2：对于多视图数据，令x1，x2，…，xv分别表示每个视图的数据矩阵，v为视图数，其中为和v＝1，…，v，dv为第v个视图的特征维度；将每一视图对应的权重定义为：

于是，将步骤1的求解问题变为：

显然，βv依赖于变量wv和s的取值，可同时计算出的wv和s用于更新βv的取值，于是可以以另一种方式优化该问题；

步骤3：采用swmpc算法求解

swmpc将问题(9)转化为通过两步迭代过程求解的过程，通过公式(8)更新变量βv，当βv的取值固定时，求解公式(9)等价于求解：

1、固定s，求解wv和f；wv和f由以下两式求得：

wv的最优解是由前mv个最小特征值所对应的特征向量所组成；f的最优解是由ls前c个最小特征值所对应的特征向量所组成；

2、固定wv和f，求解s；可通过下式求解每一向量si：

其中是以第j个元素为的列向量，有以及同公式(20)一样，该问题依旧可以得到闭式解；公式(20)与公式(27)具有同样的形式，其解也应具有同样的形式；这两式对应的拉格朗日函数为：

通过kkt条件，可以得到sij的最优解为：

其中(x)+＝max{0，x}；不失一般性，假定di1，di2，…，din是从小到大排列的，由于si是只包含k个非零值的稀疏向量，所以有sik＞0，si，k+1＝0，于是有：

由于有约束以及式(29)，可得：

将η取值代入上述不等式(30)，可以得到：

μi最大可取值为：

公式(20)与公式(27)的解可表示为：

有益效果

本发明提出的一种基于自学习权重的多视图投影聚类方法，利用结构化图学习的基本形式，将传统的权重学习方法概括为两种一般形式。通过分析它们的缺陷，最终提出了两种无参数加权多视图投影聚类方法，有效利用了不同视图的高维信息，明显提高了聚类效果。有益效果如下：

1、采用两种自学习权重的多视图投影聚类框架，无需引进难以决策且对数据集敏感的超参数，比以往方法实用性更强，同时可有效处理高维数据。

2、本发明将投影后的低维数据进行聚类，避免了噪声和冗余信息的影响，有效提升了对于高维数据的聚类效果。

3、本发明通过不断迭代优化初始构图，直接得到数据的聚类结构，有效避免了偏远项带来的不良影响，大大提升该方法对异常点的鲁棒性。

附图说明

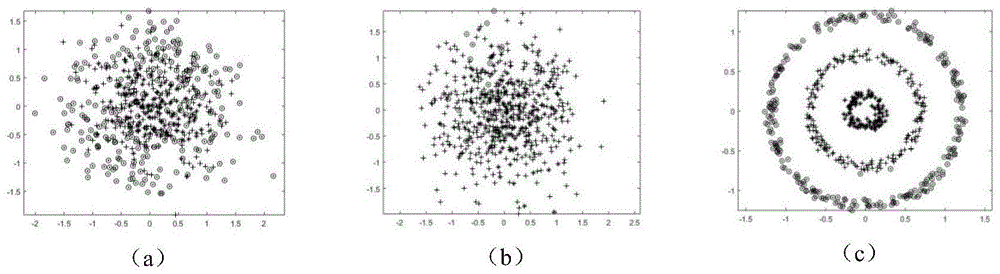
图1是不同的子空间学习方法在三个圆环数据集(包含两个维度的真实的环形数据，三个维度的噪声数据)上进行的投影效果图

图中，(a)-pca二维投影示意图；(b)-lpp二维投影示意图；(c)-本发明设计的投影结构图优化的二维投影示意图。

具体实施方式

现结合实施例、附图对本发明作进一步描述：

本发明设计了自学习权重的多视图投影聚类方法，首先利用结构化图学习的基本形式，设计了一种更为有效的子空间学习方法，之后将传统的权重学习方法概括为两种一般形式，其基本实现过程如下：

步骤一：首先对数据进行预处理，然后为统一为每个视图分配相同权值，以此构建初始的相似度矩阵。

步骤二：将初始相似度矩阵应用到本专业提出的自学习权重多视图聚类方法框架中。不断迭代优化目标函数直到收敛，再利用计算强连通分量方法，找出最优结构图中的不同聚类簇。

具体步骤如下：

1、投影结构图学习

令x＝[x1，…，xn]^t∈r^n×d表示数据矩阵，其中n是数据点的数量，d是特征的维数，每个数据点属于c类中的一类。给定数据矩阵x，每个数据点xi表示为亲和图上的顶点，并且每个边表示一对顶点的相似关系。xi和xj之间的边的权重定义为sij，表示相似度矩阵。结构图学习模型首先将相似度矩阵s定义为变量，并且可以通过解决以下问题来优化：

其中μ是正则化参数，1表示所有元素都是一的列向量。对于每个数据点xi，所有数据点{x1，x2，…，xn}都以sij大小的概率可以作为xi的近邻。较小的欧式应该被赋予较大的概率sij。正则化项用于避免公示的平凡解，即如果没有这个正则化项，只有xi本身以概率为1作为xi的近邻，而所有其他数据点不能xi的近邻。

在聚类任务中，假定需要将数据集划分为c类。如果相似度矩阵s是非负的，其所对应的拉普拉斯矩阵ls满足rank(ls)＝n-c，那么相似度矩阵s可自然将数据集划分为c个连通分量，这样就不需要后续的离散化步骤对数据集进行聚类。受此启发，在上式的基础上添加秩约束：

在许多实际应用中，会经常遇到高维数据，为了对这样的数据进行聚类，可将上式进一步扩展到以下问题：

其中表示投影矩阵，m是投影维度。st＝x^tx表示总散度矩阵，增加约束w^tstw＝i表示投影后的子空间上的数据统计不相关。

2、两种自学习权重的多视图投影聚类框架

对于多视图数据，令x1，x2，…，xv分别表示每个视图的数据矩阵，v为视图数，其中为和v＝1，…，v，dv为第v个视图的特征维度。多视图聚类方法的主要问题在于如何达到最佳的聚类效果，以及体现不同视图之间的关系。为将不同视图的信息有效整合，传统的方法是利用合适的权重将这些不同的视图线性地整合到一起，并利用额外的参数来平滑权重分布。在本发明中，提出了两种自学习权重的多视图投影聚类框架，而不像传统方法那样引入额外的参数。同时，通过将原始的高维数据的低维嵌入用于聚类任务的输入，有效避免了高维数据中包含的噪声和冗余信息的影响，提高了学习性能。

利用合适的因子权重与不同视图相结合，这样求解问题可变为：

其中α＝[α1，α2，…，αv]^t，将此方法称为除权多视图投影聚类(divisor-weightedmulti-viewprojectedclustering，dwmpc)。

接下来，本发明提出另一种无参数方法，称为自加权多视图投影聚类(self-weightedmulti-viewprojectedclustering，swmpc)，其具有以下形式：

上式并没有明确定义权重的形式，其对应的拉格朗日函数可以表示为：

其中，λ是拉格朗日乘子，来源于拉普拉斯矩阵的秩约束，z是由wv和s所组成。将以上拉格朗日函数z求导，然后令其等于0，那么有：

其中有：

显然，βv依赖于变量z的取值，公式(6)并不能直接求解。但是如果βv设置为定值，公式(6)可看成下式的解：

上式问题更容易解决，同时计算出的wv和s可用于更新βv的取值，于是可以以另一种方式优化该问题。

3、优化算法：

(1)dwmpc算法求解

令σi(ls)是ls的第i个最小特征值。很容易看出σi(ls)≥0，因为ls是正半无限的。因此，对于足够大的λ值，问题(4)相当于：

其中λ取值足够大以确保矩阵ls前c个最小的特征值为零，于是矩阵ls的秩为n-c，根据樊畿理论可知：

于是，问题可以转化为求解：

可以通过一个迭代优化算法求解上式。

3、固定αv与s，求解wv和f。由于变量wv和f相互独立，其取值可分别由以下两式求得：

公式可改写为：

由于上式对于不同的v是相互独立的，可通过下式单独求解每一视图对应的wv：

上式wv的最优解是由前mv个最小特征值所对应的特征向量所组成。公式(14)中f的最优解是由ls前c个最小特征值所对应的特征向量所组成。

4、固定αv、wv和f，求解s。公式(12)的第一项可简化表示为其中然后问题(12)变为：

在谱分析中，有一个重要而基础的公式：

利用上式，对于每一向量si，公式(17)可表示为：

其中表示矩阵s的第i行，

公式(19)可简化表示为：

其中是以第j个元素为的列向量。该公式可以得到闭式解。

3、固定wv和s，求解αv。令公式(12)可表示为：

其对应的拉格朗日函数为：

其中λα为拉格朗日乘子。通过简单的代数变换

通过以上三个步骤，交替迭代更新wv、f、s和αv，不断重复该步骤直至目标函数收敛。

(2)swmpc算法求解

swmpc将问题(5)转化为通过两步迭代过程求解的过程：通过公式(8)更新变量βv，再求解问题(9)。这里主要介绍如何求解问题(9)，求解公式(9)等价于求解：

1、固定s，求解wv和f。wv和f由以下两式求得：

wv的最优解是由前mv个最小特征值所对应的特征向量所组成。f的最优解是由ls前c个最小特征值所对应的特征向量所组成。

2、固定wv和f，求解s。可通过下式求解每一向量si：

其中是以第j个元素为的列向量，有以及同公式(20)一样，该问题依旧可以得到闭式解。公式(20)与公式(27)具有同样的形式，其解也应具有同样的形式。这两式对应的拉格朗日函数为：

通过kkt条件，可以得到sij的最优解为：

其中(x)+＝max{0，x}。不失一般性，假定di1，di2，…，din是从小到大排列的，由于si是只包含k个非零值的稀疏向量，所以有sik＞0，si，k+1＝0，于是有：

由于有约束以及式(29)，可得：

将η取值代入上述不等式(30)，可以得到：

μi最大可取值为：

公式(20)与公式(27)的解可表示为：