FRP复合材料复杂非线性弹粘塑性本构的有限元子程序算法的制作方法

本发明涉及复合材料力学性能有限元分析领域，尤其涉及frp复合材料复杂非线性弹粘塑性本构的有限元子程序算法。

背景技术：

虽然大量frp复合材料(纤维增强复合材料)已被成熟应用于航空航天、兵器装备、民用产品等诸多工业领域，但由于frp复合材料材料属性和力学行为的复杂性，现有frp结构的设计仍依赖于经验系数，导致现有frp结构刚强度设计仍趋于保守，造成了成本浪费。通过有限元软件模拟分析frp材料力学特性，是一种能有效降低复合材料结构设计开发、迭代优化的时间成本和经济成本的方式，能帮助设计人员更为精准地优化frp复合材料结构的刚强度和质量。该方法被工程设计人员广为采用，但这也要求了科研人员和工程人员开发出更多能准确地高效地描述frp复合材料复杂非线性力学特性的本构模型及其有限元子程序。

目前，已有较多的描述frp复合材料复杂非线性力学特性的本构及相应的有限元子程序算法被开发出来。近年来随着科研人员和工程人员的深入，frp复合材料在受力加载过程中呈现出的拉伸和压缩屈服行为的不对称特性、应变率相关效应、动态屈服中加载和卸载力学行为的不一致性等复杂力学行为得以发现，并在诸多期刊论文中得以分别建模描述，frp复合材料本构模型也变得愈加丰富。建立一个能综合考虑frp复合材料拉伸压缩屈服不对称性、考虑静水压力对材料屈服影响、材料应变率效应以及动态屈服后加载行为和卸载行为不一致、具有非关联流动特性的粘塑性行为的弹粘塑性本构成为一种趋势，从而用以准确地描述frp复合材料在损伤前受力加载时的复杂非线性力学特性。由于适用于现有frp复合材料非线性弹粘塑性本构的有限元子程序算法仅考虑了部分前述的复杂非线性力学行为，无法适用于求解能综合描述frp复合材料前述所有复杂非线性特性的弹粘塑性本构。

技术实现要素：

本发明提供一种frp复合材料复杂非线性弹粘塑性本构的有限元子程序算法，有效地将描述frp复合材料复杂非线性弹粘塑性力学特性的连续本构模型应用到有限元软件中。

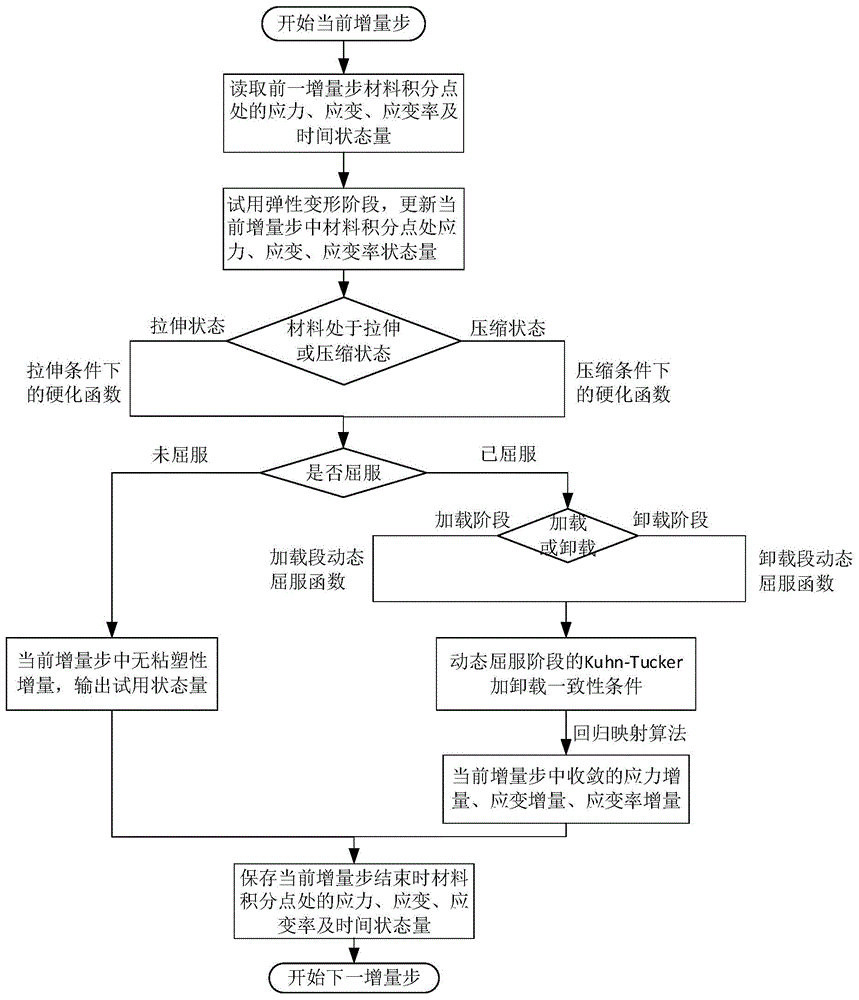
实现本发明目的的技术方案为：一种frp复合材料复杂非线性弹粘塑性本构的有限元子程序算法，包括以下步骤：

步骤1，读取前一增量步结束时材料积分点处的应力、应变、应变率及时间状态量；

步骤2，进入试用弹性变形阶段，更新当前增量步中材料积分点处应力、应变、应变率状态量，此时状态量均称为试用状态量；

步骤3，根据材料应力状态判断当前处于拉伸或压缩状态，并判断材料是否屈服：

若材料处于拉伸状态，则采用拉伸条件下的硬化函数，判断材料是否屈服；若材料处于压缩状态，则采用压缩条件下的硬化函数，判断材料是否屈服；

步骤4，若材料未屈服，则当前增量步无粘塑性应变出现，直接输出试用状态变量；

步骤5，若进入屈服状态，则判断当前材料处于加载状态或卸载状态：

若材料处于加载状态，则采用加载段的过应力函数构成动态屈服函数；若材料处于卸载状态，则采用卸载段的过应力函数构成动态屈服函数；

步骤6，基于动态屈服函数，形成动态屈服阶段的kuhn-tucker加卸载一致性条件；

步骤7，采用回归映射算法求解动态屈服后材料积分点处的应变增量、应变率增量及应力增量，更新积分点处的应力、应变、应变率和时间状态量；

步骤8，保存并输出当前增量步结束时材料积分点处的应力、应变、应变率及时间状态量，结束当前增量步的计算，并在进入下一增量步后重复前述计算过程。

与现有技术相比，本发明的有益效果为：本发明通过在判断材料屈服过程中，考虑frp复合材料拉伸和压缩屈服不对称特性的影响，首先判断材料拉伸、压缩状态，再由相应受力状态下的硬化函数构建的屈服函数判断当前的屈服行为；当材料发生屈服后，考虑frp复合材料在动态屈服后加载和卸载行为不一致的特性，区分了材料继续加载和卸载状态下的动态屈服函数，由相应加载或卸载状态下的过应力函数构建的动态屈服函数形成kuhn-tucker一致性条件，形成了能够适用于一种综合考虑frp复合材料拉伸压缩屈服不对称性、考虑静水压力对材料屈服影响、材料应变率效应以及动态屈服后加载行为和卸载行为不一致、具有非关联流动特性的复杂非线性弹粘塑性本构的有限元子程序算法，从而能更为准确地预测frp复合材料在复杂加载条件下的非线性弹粘塑性行为。

附图说明

图1为本发明frp复合材料复杂非线性弹粘塑性本构的有限元子程序算法流程图。

具体实施方式

一种frp复合材料复杂非线性弹粘塑性本构的有限元子程序算法，包括下述步骤：

步骤1、读取前一增量步结束时材料积分点处的应力、应变、应变率及时间状态量；

步骤2、进入试用弹性变形阶段，更新当前增量步中材料积分点处应力、应变、应变率状态量，此时状态量均称为试用状态量；

步骤3、根据材料应力状态判断当前处于拉伸或压缩状态，并判断材料是否屈服：

若材料处于拉伸状态，则采用拉伸条件下的硬化函数，判断材料是否屈服；若材料处于压缩状态，则采用压缩条件下的硬化函数，判断材料是否屈服；

步骤4、若材料未屈服，则当前增量步中无粘塑性应变出现，直接输出试用状态变量；

步骤5、若进入屈服状态，则判断当前材料处于加载状态或卸载状态：

若材料处于加载状态，则采用加载段的过应力函数构成动态屈服函数；若材料处于卸载状态，则采用卸载段的过应力函数构成动态屈服函数；

步骤6、基于动态屈服函数，形成动态屈服阶段的kuhn-tucker加卸载一致性条件；

步骤7、采用回归映射算法求解动态屈服后材料积分点处的应变增量、应变率增量及应力增量，更新积分点处的应力、应变、应变率和时间状态量；

步骤8、保存并输出当前增量步结束时材料积分点处的应力、应变、应变率及时间状态量，结束当前增量步的计算，并在进入下一增量步后重复前述计算过程。

所述的步骤1中，读取前一增量步即第n步结束时frp材料单元网格积分点上的应力σn、应变εn、弹性应变粘塑性应变等效粘塑性应变等效粘塑性应变率以及当前增量步即第n+1增量步的应变增量δεn+1和时间增量δtn+1，所述字符为粗体的表示矢量，上标含vp的字符表示粘塑性变量，下标含eq的字符表示等效变量；定义直角坐标系1-2-3，方向1沿着frp材料的纤维方向，方向2沿着单层frp材料平面内垂直于纤维走向的方向，方向3垂直于单层frp材料的平面，则应力σn＝[σ11,nσ22,nσ33,nσ12,nσ23,nσ13,n]^t。

所述的步骤2中，假定当前无粘塑性应变增量，材料进入试用弹性阶段，则上标含trail表示试用状态量，上标含e表示弹性变量，根据frp复合材料的宏观刚度矩阵c可得当前试用应力

所述的步骤3中，根据的值判断当前材料积分点处于拉伸还是压缩状态，若则当前材料积分点处于拉伸状态，采用由frp试件拉伸试验结果拟合得出的拉伸条件下的硬化函数以及等效应力函数构成屈服函数若则当前材料积分点处于压缩状态，采用由frp试件压缩试验结果拟合得出的压缩条件下的硬化函数以及等效应力函数构成屈服函数构成屈服函数后，判断材料积分点是否进入屈服状态。

所述的步骤4中，若则材料未进入屈服状态，则当前增量步中无粘塑性应变增量及粘塑性应变率增量出现，则输出状态变量

所述的步骤5中，若则材料进入屈服状态；读取前一增量步结束时的值，判断当前材料积分点处于加载状态还是卸载状态，所述的fn为第n个增量步中的动态屈服函数，下标i、j代表了分量，i＝1,2,3,j＝1,2,3；若则当前材料积分点处于加载状态，采用通过frp试件屈服后持续加载的实验结果拟合得出的过应力函数构建当前增量步的动态屈服函数fn+1；若则当前材料积分点处于动态屈服后的卸载状态，采用通过frp试件动态屈服后卸载的实验结果拟合得出的过应力函数构建当前增量步的动态屈服函数fn+1。

所述的步骤6中，根据构建的动态屈服函数fn+1形成动态屈服阶段的kuhn-tucker加卸载一致性条件f≤0；

所述的步骤7中，采用回归映射算法对kuhn-tucker的加卸载条件进行求解，求取当前增量步中的状态变量增量更新材料积分点处的以及当前增量步结束时的时刻tn+1。

所述的步骤8中，保存当前增量步中的应力、应变、应变率及时间状态量，包括有效应力σn+1、应变εn+1、弹性应变粘塑性应变等效粘塑性应变值等效粘塑性变化率结束当前增量步的计算，进入下一增量步后重复前述计算过程。

下面结合实施例对本发明进行详细说明。

实施例

首先需要说明本发明在实现过程中涉及到有限元软件子程序编写、有限元软件建模计算的技能，考虑到现有公知技术，本发明提供的原理说明足够本领域的技术人员通过应具备的软件编程及软件操作能力实现本发明，而不需要进行额外的创新性劳动。

本实施例提供一种综合考虑frp复合材料拉伸压缩屈服不对称性、考虑静水压力对材料屈服影响、材料应变率效应以及动态屈服后加载行为和卸载行为不一致、具有非关联流动特性的复杂非线性弹粘塑性本构，并通过针对该复杂非线性弹粘塑性本构详细解释本发明有限元子程序算法的实施流程：

所述的frp复合材料复杂非线性弹粘塑性本构如下：

在全局坐标系中建立宏观层面的复合材料应力应变关系：定义全局直角坐标系1-2-3，则纤维增强复合材料单元节点的应力变量σ＝[σ11σ22σ33σ12σ23σ13]^t，应变分量为ε＝[ε11ε22ε33γ12γ23γ13]^t，上标“t”表示矩阵的转置运算；

纤维增强复合材料单元积分处的总应变ε可分解为弹性应变ε^e及粘塑性应变ε^vp，单向复合材料的宏观刚度矩阵为c，则应力应变关系为σ＝c:ε^e＝c:(ε-ε^vp)；

考虑静水压力影响及材料拉伸压缩屈服不对称的粘塑性势函数g及等效应力函数

式中，参数a66,a44分别考虑面内剪切应力以及横向剪切应力对材料屈服的贡献，a11则考虑静水压力对材料屈服的影响。参数γ用于区分材料拉伸屈服和压缩屈服行为的不同，定义材料压缩屈服强度和拉伸屈服强度的比值为α，则γ＝2α/(α+1)。sig(x)为符号函数，若x＞0，则sig(x)＝1；若x＜0，则sig(x)＝-1；若x＝0，则sig(x)＝0。

粘塑性乘子为λ^vp，则非关联流动准则下材料的粘塑性应变增量为

屈服函数为准静态条件下各向同性硬化函数为

上标“*”表示准静态加载的变量。该各向同性硬化函数描述了材料在准静态拉伸和压缩下呈现出的不同硬化行为，kⁱ,nⁱ(i＝t,c)为材料常数。

等效粘塑性应变增量与粘塑性乘子增量之间存在联系：

frp复合材料的动态屈服函数为

其中基于过应力函数h表征等效粘塑性应变的变化率

上式中m,n为材料常数。考虑到当复合材料的应力水平超出准静态的屈服面后，复合材料在继续加载状态和卸载状态下的动态屈服行为不同，故对于材料屈服后的继续加载状态采用常数m^l，n^l，对于屈服后的应力卸载状态采用常数m^un，n^un，即

基于动态屈服面的kuhn-tucker加卸载一致性条件：

如图1所示，本实施例为针对前述上述综合考虑frp复合材料拉伸压缩屈服不对称性、考虑静水压力对材料屈服影响、材料应变率效应以及动态屈服后加载行为和卸载行为不一致、具有非关联流动特性的复杂非线性弹粘塑性本构的有限元子程序算法的具体实施流程，它包括以下流程：

步骤1、读取前一增量步结束时材料积分点处的应力、应变、应变率及时间状态量；

步骤2、进入试用弹性变形阶段，更新当前增量步中材料积分点处应力、应变、应变率状态量，此时状态量均称为试用状态量；

步骤3、根据材料应力状态判断当前处于拉伸或压缩状态，并判断材料是否屈服：若材料处于拉伸状态，则采用拉伸条件下的硬化函数，判断材料是否屈服；若材料处于压缩状态，则采用压缩条件下的硬化函数，判断材料是否屈服；

步骤4、若材料未屈服，则当前增量步中无粘塑性应变出现，直接输出试用状态变量；

步骤5、若进入屈服状态，则判断当前材料处于加载状态或卸载状态：若材料处于加载状态，则采用加载段的过应力函数构成动态屈服函数；若材料处于卸载状态，则采用卸载段的过应力函数构成动态屈服函数；

步骤6、基于动态屈服函数，形成动态屈服阶段的kuhn-tucker加卸载一致性条件；

步骤7、采用回归映射算法求解动态屈服后材料积分点处的应变增量、应变率增量及应力增量，更新积分点处的应力、应变、应变率和时间状态量；

步骤8、保存并输出当前增量步结束时材料积分点处的应力、应变、应变率及时间状态量，结束当前增量步的计算，并在进入下一增量步后重复前述计算过程；

所述的步骤1中，读取前一增量步即第n步结束时frp材料单元网格积分点上的应力σn、应变εn、弹性应变粘塑性应变等效粘塑性应变等效粘塑性应变率以及当前增量步即第n+1增量步的应变增量δεn+1和时间增量δtn+1，所述字符为粗体的表示矢量，上标含vp的字符表示粘塑性变量，下标含eq的字符表示等效变量；定义直角坐标系1-2-3，方向1沿着frp材料的纤维方向，方向2沿着单层frp材料平面内垂直于纤维走向的方向，方向3垂直于单层frp材料的平面，则当前增量步的应力σn＝[σ11,nσ22,nσ33,nσ12,nσ23,nσ13,n]^t。

所述的步骤2中，假定当前无粘塑性应变增量，材料进入试用弹性阶段，则上标含trail表示试用状态量，上标含e表示弹性变量，根据frp复合材料的宏观刚度矩阵c可得当前试用应力

所述的步骤3中，根据材料应力状态的值判断当前材料积分点处于拉伸还是压缩状态，并判断材料是否屈服：若则当前材料积分点处于拉伸状态，采用由frp试件拉伸试验结果拟合得出的硬化函数以及等效应力函数构成屈服函数若则当前材料积分点处于压缩状态，采用由frp试件压缩试验结果拟合得出的硬化函数以及等效应力函数构成屈服函数构成屈服函数后，判断材料积分点是否进入屈服状态。

所述的步骤4中，若则材料未进入屈服状态，则当前增量步中无粘塑性应变增量及粘塑性应变率增量出现，则输出状态变量

所述的步骤5中，若则材料进入屈服状态；求取前一增量步结束时的值(dσij,n为前一增量步中的应力增量)，判断当前材料积分点处于加载状态还是卸载状态，所述的fn为第n个增量步中的动态屈服函数，下标i,j代表了分量，i＝1,2,3,j＝1,2,3,；若则当前材料积分点处于加载状态，采用通过frp试件屈服后持续加载的实验结果拟合得出的过应力函数构建当前增量步的动态屈服函数若则当前材料积分点处于动态屈服后的卸载状态，采用通过frp试件动态屈服后卸载的实验结果拟合得出的过应力函数构建当前增量步的动态屈服函数

所述的步骤6中，根据构建的动态屈服函数fn+1形成动态屈服阶段的kuhn-tucker加卸载一致性条件fn+1≤0；

所述的步骤7中，采用回归映射算法对kuhn-tucker的加卸载条件进行求解，求解当前的粘塑性应变率和应变增量，即求解塑性乘子满足式中e为允许误差值可取值为10^-6，所述的回归映射算法主要基于后向欧拉积分算法和牛顿迭代法，j.c.simo及t.j.r.hughes在他们的著作《computationalinelasticity》中阐明了回归映射算法可分为最近点投影算法和切面算法，此处采用最近点投影算法求解当前增量步中的状态变量增量从而更新材料积分点处的εn+1,σn+1,以及当前增量步结束时的时刻tn+1，具体包括：

a.迭代初始步k＝0中变量初始化

b.基于牛顿迭代法在第k+1步获取则当前迭代步的粘塑性应变为等效粘塑性应变为等效粘塑性应变率为则应力为

c.判断当前迭代步是否满足若满足则求解结果收敛，输出当前迭代步所得出的粘塑性应变、等效粘塑性应变及应力值；若不满足则返回前述步骤七中的求解步b中继续进行迭代求解，直至结果收敛；

d.输出迭代求解的收敛值粘塑性应变等效粘塑性应变总应变εn+1＝εn+δεn+1，弹性应变应力至此粘塑性阶段求解结束；

所述的步骤8中，保存当前增量步中的应力、应变、应变率及时间状态量，包括有效应力σn+1、应变εn+1、弹性应变粘塑性应变等效粘塑性应变值等效粘塑性变化率结束当前增量步的计算，进入下一增量步后重复前述计算过程。