一种地球椭球面上任意图斑的面积计算方法与流程

本发明属于地球椭球面任意图斑面积计算领域，具体地说，为了避免高斯-克吕格投影变形的影响，在面积精度要求较高的应用中，需要计算土地斑块的地球椭球面面积时，使用该发明方法。

背景技术：

地球椭球面上任意图斑面积计算文献主要分为两类：一类是基于坐标直接计算，如，施一民等(2006)利用测地坐标计算了椭球面上凸多边形的面积(施一民，朱紫阳.测地坐标计算椭球面上凸多边形面积的算法[j].同济大学学报(自然科学版)，2006，34(04)：504-507)，林绿等(2007)借助空间直角坐标利用曲面积分的方法对椭球面上区域面积的计算方法进行了研究(林绿，马劲松.地球椭球面上区域面积的算法研究[j].测绘通报，2007，(06)：8-10)；另一类是基于椭球面上两条子午线和两条平行圈为界的梯形间接计算(国务院第二次全国土地调查领导小组办公室.图幅理论面积与图斑椭球面积计算公式及要求[z].2008-3-28)，该计算方法大致可以分为三个层次：顶层、中间层和底层。顶层给出整个图斑多边形的计算思路，即：多边形abcd的每一条边与任意给定经线l0围成一个大梯形图块(见图1，以ab边为例，a、b点两点沿纬线方向在经线l0上的投影点分别为a1、b1，则四边形abb1a1即为ab边与l0围成的大梯形图块)，对围成的所有大梯形图块面积计算其代数和，就得到多边形abcd的面积。中间层给出了单个大梯形图块的计算方法：把单个大梯形图块abb1a1按纬线切割，拆分成许多个小梯形图块ae1f1a1，计算其面积s1，s1累加就得到梯形图块abb1a1的面积。底层给出了小梯形图块的计算方法：转换为两条子午线和两条平行圈为界的椭球面梯形计算，使用近似计算公式计算其面积。两类面积计算方法相比较，后者更易于理解与应用。然而，第二类方法，并没有给出大梯形具体拆分的细节，具体应该拆分成多少个小梯形？或者拆分后的小梯形高等于多少合适？史守正等(2018)对该问题进行了探索性研究，研究表明，随着拆分小梯形图块的高越来越小，可以采用定积分近似计算的思路替代近似计算公式进行大梯形图块的面积计算，且计算精度逐渐增加，并获得样本梯形的高精度可靠值2661732.9601161m²(史守正，石忆邵，赵伟.椭球面上图斑面积计算方法的改进[j].武汉大学学报·信息科学版，2018，43(5)：779-785)。

技术问题：计算任意椭球面图斑面积需要计算大梯形图块面积，而大梯形图块面积计算精度依赖于小梯形的近似无限拆分，以及小梯形的面积计算。椭球面小梯形面积计算实质上是利用椭球面梯形来完成的，椭球面梯形面积公式有精确计算公式和近似计算公式之分，在使用自变量和返回值均为双精度浮点数的系统函数的前提下，采用近似计算公式计算精度较高。然而，双精度浮点数只有15-16位有效数字，对于单个椭球面梯形面积计算而言精度尚可，对于近似无限拆分的小梯形而言，该精度可能影响其累加后的大梯形面积精度。迄今为止，椭球面上任意图斑的面积计算仅仅局限于理论探索阶段，国内主流的gis软件supermap及国际知名gis软件arcgis均没有提供可用的图斑椭球面面积的计算功能。

为此，我整合现有椭球面图斑面积间接计算的知识，发明了一种地球椭球面上任意图斑的面积计算方法，并通过实例验证了该方法的可靠性，若gis软件采用该方法，则可以精确地计算任意图斑的地球椭球面面积。

技术实现要素：

该发明使用椭球面梯形间接计算任意图斑面积，计算方法大致可以分为三个层次：顶层、中间层和底层。

顶层思路与文献相一致(国务院第二次全国土地调查领导小组办公室.图幅理论面积与图斑椭球面积计算公式及要求[z].2008-3-28)，对于任意图斑多边形，拆分成与其边数相等的数个大梯形图块，计算所有大梯形图块的面积代数和，即得到任意图斑的面积。

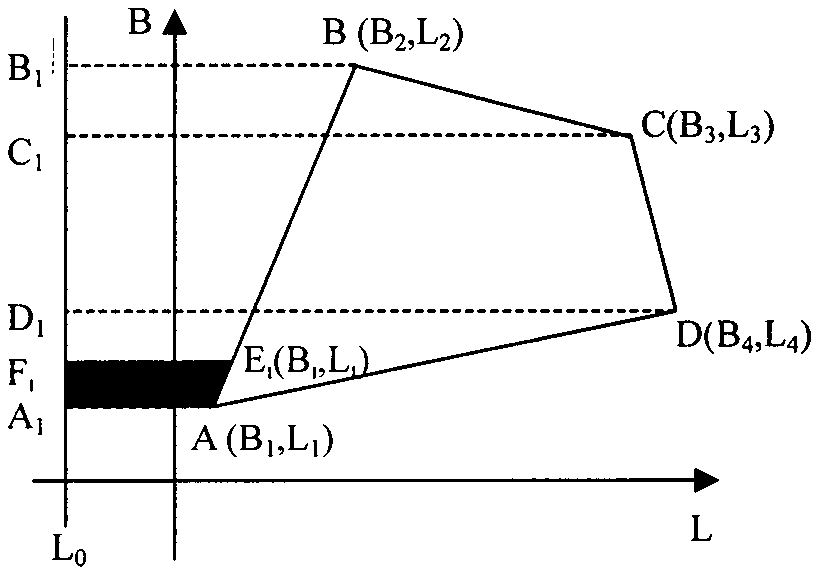
中间层，采用专利申请号201910046051.0的说明书中的方法，计算大梯形图块的面积。不失一般性，以图1中大梯形图块abb1a1为例，说明该方法。取ab边的中点为e((b1+b2)/2，(l1+l2)/2，)，e点沿经线方向在纬线b1、b2上的投影点分别为ea、eb(见图2)，通过经线eaeb对原大梯形图块进行切割，用切割掉的经线右边的阴影三角形δebeb来填补经线左边的空白三角形δeaea，则椭球面大梯形图块变换为椭球面梯形eaebb1a1，该椭球面梯形面积为大梯形图块的近似估计值。换个思路来讲，大梯形图块面积真值可以精确表达为椭球面梯形面积(近似估计值)减去空白三角形面积，再加上阴影三角形面积，即：

s大梯形图块abb1a1＝s梯形eaebb1a1-sδeaea+sδebeb

对阴影三角形和空白三角形再审视发现，二者均可以视为椭球面大梯形的特例，其面积计算方法与常规椭球面大梯形完全一致。阴影三角形和空白三角形的一条经线边可以视为大梯形中的l0边，二者的一条纬线边对应大梯形的一条纬线边，二者斜边的另一个顶点则对应于大梯形的另一条纬线边，只是该边长度退化为0，这样，割补中产生的阴影三角形和空白三角形就可以被视为短底边退化为0长度的大梯形，因此，也可以通过对斜边的割补，转化为椭球面梯形(见图2)，使用大梯形图块面积计算真值表达式进行计算。该算法的实现在于递归，两个底、高均缩小的椭球面大梯形面积(阴影三角形和空白三角形作为大梯形的特例，被归类为椭球面大梯形)递归调用原椭球面大梯形图块面积计算表达式进行计算。

底层给出椭球面梯形的高精度计算方法。椭球面梯形的面积公式主要有四个，一个精确计算公式和三个等价的近似计算公式(史守正，石忆邵，赵伟.椭球面上图斑面积计算方法的改进[j].武汉大学学报·信息科学版，2018，43(5)：779-785)。所有四个公式均来源于以下积分表达式：

式中，t为椭球面梯形面积，l1、l2和b1、b2分别为围成该梯形的两条经线和纬线，a为椭球长半轴(单位：m)，b为椭球短半轴(单位：m)，e为第一偏心率，e²＝(a²-b²)/a²。

对该积分直接进行求解，即得到精确计算公式：

而对该积分公式先进行幂级数展开，再进行分项积分，整理，即可获得三个理论等价的近似计算公式。其中又以国务院第二次全国土地调查领导小组办公室推荐的近似计算公式最为常用，具体公式如下：

其中a、b、c、d、e为常数，按下式计算

a＝1+(3/6)e²+(30/80)e⁴+(35/112)e⁶+(630/2304)e⁸

b＝(1/6)e²+(15/80)e⁴+(21/112)e⁶+(420/2304)e⁸

c＝(3/80)e⁴+(7/112)e⁶+(180/2304)e⁸

d＝(1/112)e⁶+(45/2304)e⁸

e＝(5/2304)e⁸

式中，a为椭球长半轴(单位：m)，b为椭球短半轴(单位：m)，e为第一偏心率，e²＝(a²-b²)/a²，δl为梯形图块经差(单位：弧度)，(b2-b1)为梯形图块纬差(单位：弧度)，bm＝(b1+b2)/2。

与近似计算公式相比较，精确计算公式需要额外使用对数运算、开平方运算等函数。由于计算机默认的系统函数的变量及返回值均为双精度浮点数，只有15-16位有效数字，导致精确计算公式的计算精度不如近似计算公式。

本方法另辟蹊径，全面使用多达28-29位有效数字的十进制变量，提高公式中正弦函数、余弦函数、自然对数函数等所有函数的返回值精度到十进制数变量水平，此时，椭球面精确计算公式的面积计算精度大大提高，而近似计算公式却受制于e的高次方项的舍弃，计算误差改进不明显，纵然近似计算公式取至e¹⁰项，其计算精度也远低于精确计算公式。

面积公式中使用的高精度函数算法如下：

对数函数采用幂级数近似计算，具体公式为：

具体c#代码实现如下：

开平方函数使用牛顿迭代法。计算正数a的平方根等价于计算方程f(x)＝x²-a＝0的解，求取方程近似解的经典算法是牛顿迭代法，其迭代公式为：xn+1＝(xn+a/xn)/2。

牛顿迭代法原理解释为：设函数f(x)上某一点的坐标为(x0，y0)，过该点的切线方程为y＝kx+b，令y＝0，则可以计算出切线与x轴的交点横坐标x＝-b/k，而b＝y0-kx0，y0＝x0²-a，k＝2x0，交点横坐标可以化简为x＝(x0+a/x0)/2。记x1＝(x0+a/x0)/2，继续求过点(x1，f(x1))的切线与x轴的交点的横坐标x2＝(x1+a/x1)/2，显然，x2比x1更靠近f(x)函数曲线与x轴的交点，即：x2比x1更接近方程f(x)＝0的解。继续迭代，平方根的计算精度逐步提高。

令x0＝a，开平方函数的具体c#代码实现如下：

正弦函数计算用到泰勒级数，公式为：

其具体c#代码实现如下：

π常数使用了π值的小数点后30位记忆歌谣：“山巅一寺一壶酒(3.14159)，尔乐苦煞吾(26535)，把酒吃(897)，酒杀尔(932)，杀不死(384)，遛尔遛死(6264)，扇扇刮(338)，扇耳吃酒(3279)。”

定义π值常数为3.141592653589793238462643383279m，共31位有效数字。程序调试过程中变量取值监测显示：系统实际使用的十进制数pai_math2取值为3.1415926535897932384626433833，共29位有效数字。

新方法的计算流程为：

(1)构造函数caltrap(l1，l2，b1，b2)，计算椭球面梯形面积。该函数使用椭球面梯形精确计算公式：

两条经线和两条纬线界定一个椭球面梯形，不妨假设该椭球面梯形的左下角点经纬度坐标为(l1，b1)，右上角点经纬度坐标为(l2，b2)，则(l2-l1)＞0，(b2-b1)＞0，椭球面梯形面积公式计算结果为正。这对于计算单个梯形图块面积没任何问题，但是，任意图斑面积计算思路的顶层需要各大梯形图块的面积代数和，即计算过程中有些梯形的面积值需要负数，为此，对该面积公式进行再审视。

设(l1，b1)和(l2，b2)为椭球面上的任意两点，当(l1-l2)*(b1-b2)＝0时，只有一条经线或者纬线无法真正围成椭球面梯形，即椭球面梯形面积为0值；当(l1-l2)*(b1-b2)＞0时，依公式，椭球面梯形获得正的面积值；而当(l1-l2)*(b1-b2)＜0时，椭球面梯形获得负的面积值。

(2)构造递归函数calpatch(l0，l1，b1，l2，b2，err)，计算大梯形面积。

与椭球面梯形面积计算中的四个参数不同，椭球面大梯形图块面积计算需要六个参数，以图2为例，(b1，l1)为a点坐标，(b2，l2)为b点坐标，l0为图2中的l0经线(不妨假定l0选择在大梯形的左侧，比如：可以使用图层范围的最小经度值作l0)，l0经线与ab边及过ab的两条平行圈围成椭球面大梯形abb1a1，err为精度控制变量，以平方米为单位(比如err＝1m²)。对该大梯形进行割补，转换为椭球面梯形，当转换后的椭球面梯形面积大于控制变量err时，进行递归运算，反之，终止递归。显然，新梯形的两条经线分别为l0，(l1+l2)/2，两条纬线分别为b1，b2，具体递归函数如下：

calpatch(l0，l1，b1，l2，b2，err)

{

//本函数用来计算椭球面大梯形图块的面积

sum＝caltrap(l0，(l1+l2)/2，b1，b2)；//计算椭球面大梯形面积估计值(椭球面梯形面积)

if(math.abs(sum)＜err)//当估计值(包含割补的小三角形)的绝对值小于指定值err时，不再递归returnsum；

else//反之，递归计算

returnsum+calpatch((l1+l2)/2，l1，b1，(l1+l2)/2，(b1+b2)/2，err)+calpatch((l1+l2)/2，(l1+l2)/2，(b1+b2)/2，l2，b2，err)；//大梯形面积真值＝大梯形面积估计值+阴影三角形面积-空白三角形面积。其中，calpatch((l1+l2)/2，l1，b1，(l1+l2)/2，(b1+b2)/2，err)为空白三角形面积，其值为负，calpatch((l1+l2)/2，(l1+l2)/2，(b1+b2)/2，l2，b2，err)为阴影三角形面积，其值为正。

}

(3)构造累加函数calallpatch(l0，ls，bs)，累加各组成大梯形面积的代数和，得到任意图斑的椭球面面积。计算时，需要指定l0经线数值，以及任意图斑各顶点的经纬度坐标(ls，bs)。

calallpatch(l0，ls，bs)

{

l1＝ls[0]；b1＝bs[0]；//图斑的第一个顶点坐标，也是第一个大梯形的顶点

sum＝0；//存放任意图斑面积

for(i＝1；i＜ls.length；i++)//依次求解各组成大梯形面积并累加

{

l2＝ls[i]；b2＝bs[i]；//大梯形的第二个顶点坐标

sum＝sum+calpatch(l0，l1，b1，l2，b2，err)//面积累加

l1＝ls[i]；b1＝bs[i]；//大梯形的第一个顶点坐标

}

l2＝ls[0]；b2＝bs[0]；//最后一个大梯形的第二个顶点，图斑的第一个顶点坐标

sum＝sum+calpatch(l0，l1，b1，l2，b2，err)//面积累加

sum＝-sum；//确保顺时针多边形面积为正，逆时针多边形面积为负

}

新方法的优势：

新方法给出一种简单可行的椭球面上任意图斑的面积计算方法；该方法计算过程易于理解，计算方法易于计算机实现，通过控制变量err的大小，可以方便地控制椭球面上任意图斑的面积计算精度。此外，顺时针多边形面积计算结果为正，逆时针多边形面积计算结果为负，稍作调整，该方法能够适应含岛屿的多边形面积计算。

附图说明

图1：椭球面上任意多边形计算面积(国务院第二次全国土地调查领导小组办公室.2008)

图2：椭球面上大梯形图块计算面积

图3：椭球面上任意图斑计算面积实例

具体实施方式

具体实施分两部分，第一部分验证椭球面梯形面积精确计算公式的精度(算法的底层部分)，第二部分给出一个任意图斑面积计算的例子(算法的中间层和顶层)。

第一部分：不失一般性，使用西安80椭球参数，在史守正等(2018)计算过的四个经纬度点围成的椭球面梯形为计算对象，具体坐标见表1。

表1西安80椭球4个点的坐标经纬度

分别利用精确公式与近似计算公式计算其椭球面面积，运算过程中，近似计算公式也全部使用自编函数提升至十进制数精度水平(或者10^-28精度水平)。近似计算公式选取国务院第二次全国土地调查领导小组推荐的乘积项公式，并计算至e¹⁰项，近似计算公式的计算值为2661732.9601182273781954774308m²，而样本梯形面积的精确公式计算值为2661732.9601182342785799189m²，从高位到低位，二者前14位有效数字相同，且与史守正等(2018)使用系统函数(其函数自变量和返回值均为双精度类型变量)的计算值2661732.9601182m²相同。

从15位有效数字起，精确公式与近似计算公式出现差异。为评判二者精度差异，引入史守正等(2018)使用的改进矩形法公式，抛开精确计算公式和近似计算公式，直接使用定积分的近似算法计算椭球面梯形面积，计算过程中的函数取值仍然使用高精度的自编函数。具体计算结果见表2

表24个点在西安80椭球上的等角航线面积

注：椭球面梯形面积计算过程中，改进矩形法需要指定δb取值大小，乘积项和精确公式则不需要

改进矩形法是参照定积分近似计算思想构建而成，通过缩小切割小梯形的高δb，增加大梯形的切割次数，逐步提高计算精度。较少切割次数与较高切割次数的计算结果相比较，二者相同的有效数字位数为计算结果的可靠值。当δb＝10^-3时(约206″)，样本梯形未被切割；当δb＝10^-4时(约20.6″)，样本梯形被切割两次，改进矩形法计算的可靠值为2661732.9m²；当δb＝10^-5时，改进矩形法计算的可靠值为2661732.960；当δb＝10^-6时，改进矩形法计算的可靠值为2661732.960118m²；当δb＝10^-7时，改进矩形法计算的可靠值为2661732.96011823m²；当δb＝10^-12时，改进矩形法计算的可靠值为2661732.96011823427857992m²；在δb从10^-3缩小到10^-12的过程中，计算结果逐渐增加，而当δb＝10^-13时，笔者电脑程序运行时间大于14小时，计算结果较δb＝10^-12时反而减少，不再符合数值增加的趋势，究其原因，概因为累加单项小梯形面积数值过小，从而导致精度损失所致。

对比改进矩形法的计算结果可知，精确公式获得的样本梯形面积可靠值为2661732.9601182342785799m²，拥有23位有效数字，远远优于乘积项近似公式的14位有效数字。虽然，乘积项近似计算公式(10)式仅取至e¹⁰项，增加e¹²项、e¹⁴项可以提高其精度，但是，诚如此，近似计算公式的所有参数需要重新计算，远不如直接使用精确公式更方便。

若参照esriarcgis软件，投影坐标系的默认坐标分辨率值0.0001m，对应图斑面积计算需要精确到10^-8m²，这对应于该样本椭球面梯形而言，需要保留15位有效数字。但是，在任意图斑的面积计算中，各大梯形图块面积计算时，需要近似无数次调用该椭球面梯形面积公式，以累加获得大梯形图块的面积，进而累加获得任意图斑的面积。无数次的累加必然带来精度的损失，因此，在任意图斑的面积计算中，取至e¹⁰项的椭球面梯形面积近似计算公式只能确保14位有效数字是不够的，使用高精度的函数提升精确计算公式精度到23位有效数字是有必要的。

第二部分：不失一般性，使用西安80椭球参数，在史守正等(2018)计算过的椭球面大梯形的2、4点以外增加5号点，组成三边均不沿经纬线方向的三角形作为实例进行验证(见图3)。该三角形图斑具体坐标数值见表3，设2、4两点沿纬线方向在过5号点的子午线(l0＝116°22′00″)上的投影点分别为p’2、p’4，则算法顶层图斑三角形p2p4p5的面积可以表示为

s图斑三角形p2p4p5＝s梯形p2p4p’4p’2+s梯形p4p5p’4+s梯形p5p2p’2

其中，后两个三角形，可以视为特殊的椭球面梯形(史守正，2018)，计算方法与一般的椭球面梯形相同。

表3西安80椭球3个点的坐标经纬度

算法中间层采用专利申请号201910046051.0的说明书中的思路，利用递归计算大梯形图块的面积。与椭球面梯形利用公式直接获得23位有效数字的高精度面积值不同，椭球面大梯形面积计算总是需要切割成小梯形以提高计算精度。在一定精度范围内，椭球面大梯形面积随切割小梯形高的缩小，而精度提高(或者说，随err变量的取值减小，精度提高，一般而言，err缩小10倍，面积精度提高1位)。另一方面，随着切割小梯形的高的缩小，程序计算量增加。本实例在计算图3所示图斑三角形p2p4p5的各组成大梯形图块面积时，若err变量取值10^-4m²，面积为-3993066.3359626475022751453142m²；若err变量取值10^-5m²，面积为3993066.3359626514660603331232m²。若计算结果采用四舍五入取值到10^-8，二者均为-3993066.33596265m²。考虑计算效率及当今的mm级坐标定位精度，err变量取值10^-4m²，图斑面积计算精度足够使用。err变量取值10^-4m²时，本实例计算过程中各组成大梯形图块面积计算结果见表4。

表4椭球面上任意图斑计算面积实例单位：m²

注：1逆时针多边形面积为负；2：err＝0.0001m²

综上，本发明给出了一个任意图斑面积计算的方法，并通过实例进行了验证，实践表明，该方法简单明了，易于计算机实现。