各向同性固体材料的静态热弹性问题求解方法以及装置与流程

本发明属于固体力学技术领域，具体涉及一种各向同性固体材料的静态热弹性问题求解方法以及装置。

背景技术：

各向同性材料在日常生活中，各大工程结构中普遍存在，而热弹性力学是工程中经常遇到的问题，对于极其炎热或寒冷的环境条件，分析材料结构由于温度变化带来的影响非常关键，该问题也受到了国内外学者的关注。以工程建筑中常用的玻璃为例，在现代化城市建设中，许多大型地标建筑外体会用到大量的玻璃材料，玻璃材料即为各向同性材料，因而玻璃结构的安全性更需要重视，然而对玻璃安全性具有影响的因素中，极为重要一个因素就是温度，温度等因素会影响玻璃在实际温度工况下产生的位移和应力，进而对结构的安全产生重要影响，因此，获得这些因素对材料的影响情况显得尤为重要，这就涉及到材料的热弹性力学问题求解。

在利用边界元处理热弹性力学问题时，积分方程中会出现域积分。目前通常采用边界元法来进行求解，与有限元法相比边界元法的一个优点是可以将问题降低一维。边界元法可以节省大量的计算资源和时间，因为只需要对边界进行网格划分，并且模型重建过程也较为简单。然而，由于边界积分方程(bie)无法知道域中的信息，并且对于非齐次问题存在域积分，这一优点也是其缺点。同样的缺点也存在于许多其他的边界类型方法中，如边界节点法(bnm)、伽辽金边界节点法(gbnm)和混合边界节点法(混合bnm)。

边界元法中域积分的计算方法很多。用体积元划分域和计算体积元中的域积分可能是最自然的方法。与双互易法(drm)等其他方法相比，直接体积积分法是计算域积分的一种明显更好的选择。然而，边界元法将失去只用单元进行边界离散化的优势。因此，许多研究者都将注意力集中在避免体积元素的方法上，目前已经提出了几种方法，如双互易法(drm)。在drm中，非齐次项可以用径向基函数(rbf)等一系列函数来逼近，并应用第二个互易性将域积分转化为边界积分。只有域或边界上的点需要提供由非齐次项表述的信息。然而，drm的精度在很大程度上取决于域点的分布和位置，以及用于近似非齐次项的函数类型。此外，复杂域中的点的排列并不容易。

技术实现要素：

本发明是为了解决上述问题而进行的，目的在于提供各向同性固体材料的静态热弹性问题求解方法以及装置，能够获得结构的位移、应力和面力变化数据，具有极高的准确性和有效性。

本发明为了实现上述目的，采用了以下方案：

<方法>

本发明提供一种各向同性固体材料的静态热弹性问题求解方法，其特征在于，包括：

步骤1：基于实际待求解结构的材料参数、网格化分数、网格类型以及边界条件信息，建立该待求解结构的数值模型，并对数值模型的每个单元上的节点进添加材料参数和边界条件信息；

步骤2：建立应变和应力方程

各向同性弹性体材料其总的应变εij和应力σij之间的关系式为：

式中，θ为温度的变化值；β为热膨胀系数；g为剪切模量；ν为泊松比；

i,j,k为取值1～2的整数；δij为kronecker符号：

应力σij的表达式为：

式中，λ为lame系数；

步骤3：建立位移积分方程

位移边界方程为：

式中，γ为问题研究域ω的边界；uij(x,y)和tij(x,y)是开尔文解，可写为：

式中，x和y分别代表源点和场点；r代表源点和场点之间的距离；代表距离关于x的导数；

步骤4：建立内部应力积分方程

式中

而当x∈γ，可得面力边界积分方程：

cij(x)tj(x)＝cij(x)σij(x)nj(x),x∈γ(11)

步骤5：将域积分转化为边界积分

对于公式(3)中的域积分d1＝∫ωφi(x,y)βθ(y)dω(y)，和公式(6)中的域积分d2＝∫ωβ[θ(y)-θ(x)]φij(x,y)dω(y)，利用如下公式转化为等效边界积分：

其中y＝(y1,y2)∈ω0，k(x,y)是定义在域内，对任意x,y∈ω⁰，x≠y都连续的微奇异核函数，并且对于x,y∈ω⁰，x≠y，都存在一个常数c1使得

|k(x,y)|≤c1r^-β,0≤β＜3(14)

其中r＝|x-y|，ni是边界γ上外法向量n在yi-axis方向上的元素，g(y)代表在任意包含ω0的矩形区域b内f(y)的延续，并且g(y)在区域b/ω0内有界且连续，函数a＝a(y2)和b＝b(y1)是有界的，t{t,y2}∈b；

为了简化问题，所有起始点可以定义在同一个直线{yl1＝m}上，a＝a(yl2)＝m为任意常数值，l1和l2分别取1和2中不同值，把边界离散为n个单元，这样公式(12)可以写为：

其中γi为第i个边界单元，并且

对于单元e来讲，若点x处于由单元e产生的积分区域内，则存在微奇异积分，进而积分线l{yl2＝xl2}会和单元e会存在一个交点s，称为边界单元e上微奇异积分的奇异点，进而，公式(15)可以写成：

其中

式中，代表第i个边界积分点，m代表积分点的个数，wi和分别代表第i个边界积分点在yl1方向的权重和外法向量；

步骤6：建立遍及积分方程的求解矩阵

经过离散，除去域积分的位移边界积分方程可写为如下形式

其中，γe为e个单元的边界，并且

将cij(p)整合到公式右边的第二项中去即可的以下矩阵方程：

hu＝gt(21)

将已知的边界条件代入上式，即可得

ax＝y(22)

采用同样的离散方式可得应力的矩阵方程

σ(p)＝g^o(p)t-h^σ(p)u(23)

然后，利用高斯消去求解法即可得到模型的边界和内部点的变化数据，作为待求解结构的边界和内部点的变化数据。

进一步，本发明所提供的各向同性固体材料的静态热弹性问题求解方法，还可以具有这样的特征：步骤1中边界条件包括边界位移和面力，步骤6中求解得到的变化数据为包含边界位移、面力、应力变化情况以及内部位移和应力变化情况的数据。

<装置>

另外，本发明还提供了一种各向同性固体材料的静态热弹性问题求解装置，其特征在于，包括：求解模块，根据上文<方法>中所描述的各向同性固体材料的静态热弹性问题求解方法得到待求解结构的边界和内部点的变化数据；和输入显示模块，让操作者输入待求解结构的材料参数、网格化分数、网格类型以及边界条件信息，并对求解结果进行显示。

发明的作用与效果

根据本发明所提供的各向同性固体材料的静态热弹性问题求解方法以及装置，能够容易地求解出玻璃等各向同性固体材料在实际温度工况下产生的位移和应力等参数，求解结果具有极高的准确性和有效性，进而能够有效地用于实际工程中分析材料结构由于温度变化带来的影响，以确保工程结构的安全性和可靠性。

附图说明

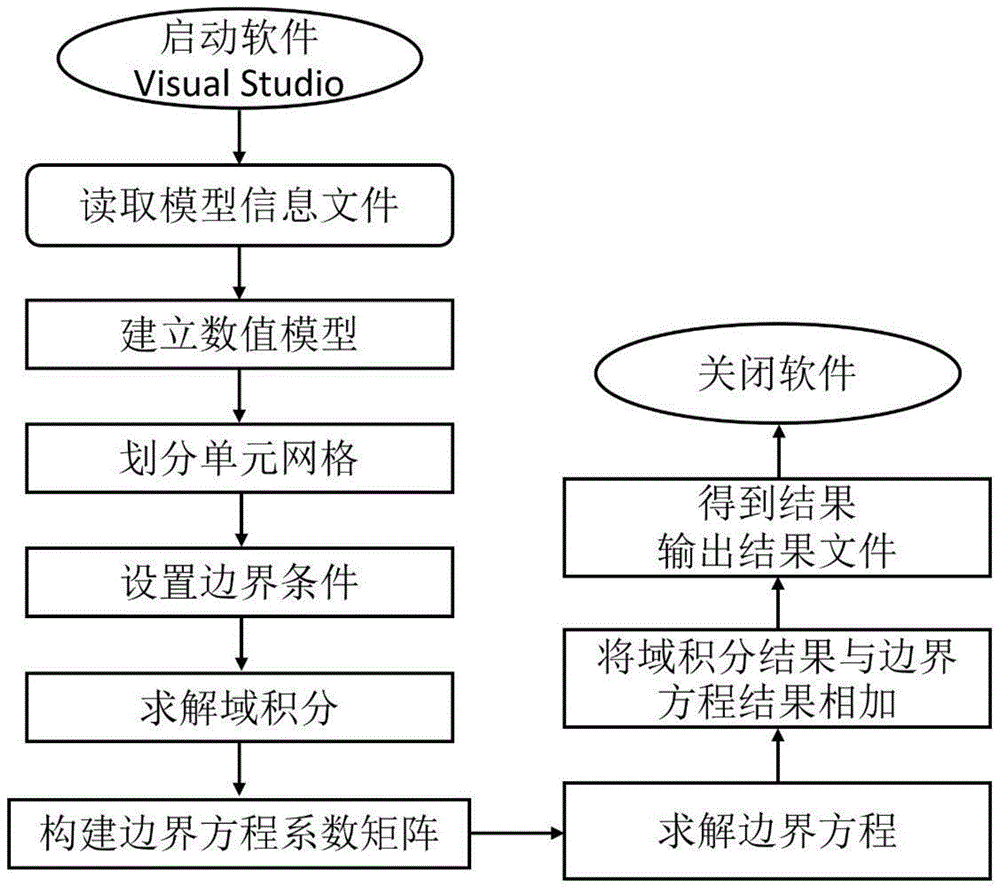
图1为本发明实施例中涉及的各向同性固体材料的静态热弹性问题求解方法的流程图；

图2为本发明实施例中涉及的模型及其边界条件示意图；

图3为本发明实施例中涉及的常规积分和微奇异积分的示意图；

图4为本发明实施例中涉及的边界元法计算所得纵向位移与精确解对比图；

图5为本发明实施例中涉及的边界元法计算所得正应力与精确解对比图。

具体实施方式

以下结合附图对本发明涉及的各向同性固体材料的静态热弹性问题求解方法以及装置的具体实施方案进行详细地说明。

<实施例>

如图1所示，本实施例所提供的各向同性固体材料的静态热弹性问题求解方法方法包括以下步骤：

步骤1：利用ug软件建立待求解模型，输入模型的材料参数、单元类型、单元划分数量以及边界条件等信息，然后输出.inp格式的模型数据信息文件。其中，输入模型参数和导出数值模型的方法为利用个人开发的关联ug的cae可视化界面程序；输入模型参数具体包括模型的弹性模量和泊松比，所需输入的边界条件包括已知的边界位移和面力；类型为.inp输出文件中包括模型的坐标信息、边界条件、设定的单元划分数量、材料参数、单元类型等。

本实施例中为验证准确性及有效性，选取一个具有解析解的计算模型，如图2所示该模型为一个玻璃矩形板，设其弹性模量为e＝10000mpa，泊松比为v＝0.3，热膨胀系数为k＝0.00001k^-1，矩形板的长度和宽度为w＝2m和h＝1m，其边界条件正如图2所示，温度场分布函数给定为以下形式：

θ＝c2y²+c1y+c0(i)

其中，c2＝40，c1＝－60,c1＝0。

y方向的位移uy和内部正应力σxx解析解公式为：

步骤2：将基于bem和lim，利用c++语言编写的静态热弹性力学问题求解程序在visualstudio上运行，调用模型的数据信息文件；在运行程序时，会首先调用个人开发的cae可视化界面程序，读取输入文件，提交任务，并继续进行。

步骤3：在程序运行过程中，首先对模型进行数值模型建立，接着对数值模型的每个单元上的节点进添加材料参数和边界条件等信息。

步骤4：然后结合bem和lim建立的静力热弹性力学问题的求解方程，进一步离散化。利用lim求解边界积分方程中的域积分。然后建立边界积分的系数矩阵，形成针对未知量的系数矩阵形成类似ax＝y的的求解方程，然后将求解方程所得结果加上域积分所得结果即为所需要求解的结果(包括面力、应力和位移)。结合一些存在理论解的模型进行对比，可以证明本发明的精确性和有效性。解析公式的建立、离散化，并整合系数矩阵，得到求解方程，其具体实现包括以下子步骤：

步骤4.1：建立控制方程；

对于各向同性弹性体内，温度场会造成结构发成体积变形，而结合前人研究可知总的应变和应力之间的关系为：

其中，θ为温度的变化值；β为热膨胀系数；g为剪切模量；ν为泊松比；公式右边前两项是指由于应力变化产生的体积变形，而第三项则是由于温度带来的影响。

同样的，可以得到应力的表达式：

式中，λ为lame系数，i,j,k为取值1～2的整数。

此外，公式(1)可以转化为以下控制方程的形式：

步骤4.2：建立位移积分方程；

结合贝蒂互易理论，可以得到以下位移边界方程：

其中，γ为问题研究域ω的边界；uij(x,y)和tij(x,y)是开尔文解，可写为：

和

其中，x和y分别代表源点和场点；r代表源点和场点之间的距离；代

表距离关于x的导数；δij为kronecker符号，可写为：

由此可以得到：

式中

显而易见，式(9)中，存在一处域积分：

d1＝∫ωφi(x,y)βθ(y)dω(y)(11)

步骤4.3：建立内部应力积分方程；

结合公式(2)和如下应力应变关系公式：

可得

其中，可知

显而易见，在式(14)中存在强奇异积分，为了解决这个问题，将其转换为如下公式：

其中

而当x∈γ，可得面力边界积分方程

cij(x)tj(x)＝cij(x)σij(x)nj(x),x∈γ(20)

观察公式(15)可得存在一项域积分：

d2＝∫ωβ[θ(y)-θ(x)]φij(x,y)dω(y)(21)

步骤4.4：利用lim将域积分转化为边界积分；

为了保证bem只需要离散边界的优越性，需要把(11)和(21)这两项域积分转换为边界积分。根据直线积分法，域被积函数f(y)是定义在问题域ω0上的，可以利用如下公式转化为等效边界积分：

以上公式是针对二维问题的表达式，其中y＝(y1,y2)∈ω0，k(x,y)是定义在域内，对任意x,y∈ω⁰，x≠y都连续的微奇异核函数，并且对于x,y∈ω⁰，x≠y，都存在一个常数c1使得

|k(x,y)|≤c1r^-β,0≤β＜3(24)

其中，r＝|x-y|，ni是边界γ上外法向量n在yi-axis方向上的元素，g(y)代表在任意包含ω0的矩形区域b内f(y)的延续，并且g(y)在区域b/ω0内有界且连续，函数a＝a(y2)和b＝b(y1)是有界的，t{t,y2}∈b。

以y1-direction为例，为了简化问题，所有起始点可以定义在同一个直线{y1＝m}上，也就是说，a＝a(y2)＝m为任意常数值，可以把边界离散为n个单元，这样公式(22)可以写为

其中，γi为第i个边界单元，并且

如图3所示，积分项可以分为两部分，常规积分项和微奇异积分项，一般来说，对于单元e来讲，如果点x处于由单元e产生的积分区域内，则存在微奇异积分，进而积分线l{y2＝x2}会和单元e会存在一个交点s，称为边界单元e上微奇异积分的奇异点，进而，公式(25)可以写成：

其中

式中，代表第i个边界积分点，m代表积分点的个数，wi和分别代表第i个边界积分点在y1-direction方向的权重和外法向量。

如果点x不处于由单元e产生的积分区域内，则采用常规积分处理。

步骤4.5：建立遍及积分方程的求解矩阵；

经过离散，除去域积分的位移边界积分方程可写为如下形式

其中，γe为e个单元的边界，并且

则式(29)可转化为

将cij(p)整合到公式右边的第二项中去即可的以下矩阵方程：

hu＝gt(32)

将已知的边界条件代入上式，即可得

ax＝y(33)

采用同样的离散方式同样可得应力的矩阵方程

σ(p)＝g^o(p)t-h^σ(p)u(34)

然后利用高斯消去求解法即可得到所求未知量，本实施例中，仅以比较有代表性的纵向位移和正应力为例对求解结果进行说明。

图4为计算模型的y方向位移uy在y方向的变化，图5为计算模型的y方向位移σxx在y方向的变化，可见计算结果与解析解高精度吻合，通过利用下式进行误差分析，可得纵向位移和正应力σxx的误差分别仅为0.083％和0.29％。

其中，和分别代表精确解和计算值，n为选取节点个数。

基于以上计算得到数据，通过结合温度产生的影响，在玻璃结构安装设计中，预设玻璃结构的安装框架余量，进而防止玻璃结构因为温度过低或者过高而发生爆裂等造成建筑结构失稳以及威胁人类生命安全的负面结果。

另外，以上过程还可以采用各向同性固体材料的静态热弹性问题求解装置来实现，该装置应包括输入显示模块和求解模块。对于需要输入和显示的内容通过输入显示模块进行处理，例如让操作者输入待求解结构的材料参数、网格化分数、网格类型以及边界条件信息，并对求解结果进行显示；对于其它进行计算和求解的内容通过求解模块进行处理。

以上实施例仅仅是对本发明技术方案所做的举例说明。本发明所涉及的各向同性固体材料的静态热弹性问题求解方法以及装置并不仅仅限定于在以上实施例中所描述的内容，而是以权利要求所限定的范围为准。本发明所属领域技术人员在该实施例的基础上所做的任何修改或补充或等效替换，都在本发明的权利要求所要求保护的范围内。