二元翼型非线性颤振时域模型的建模方法与流程

本发明涉及一种建模方法，特别涉及二元翼型非线性颤振时域模型的建模方法，属于非线性振动技术领域。

背景技术：

工程实际中，如水翼艇的水翼，潜艇中的舵翼等船舶构件作为动力学系统，结构参数设计不当时，在流场中高速运动会产生颤振现象导致结构破坏，或发生持续的弱振动现象诱发水噪声，降低水下航行器的隐蔽性。国内外学者对于舵系统或者水翼的水弹性研究，多数采用二元颤振模型，或者单个水翼加一根扭簧等简化模型来进行理论计算分析。对于二元颤振模型的计算中，关键在于如何获得二元颤振模型的计算参数。在早期的计算中，舵叶往往处理成刚体，采用舵轴的等效弹簧刚度、等效扭簧刚度作为二元颤振模型中的弹簧和扭簧，从而建立二元颤振模型。近期研究中，学者们逐渐将舵叶等水翼结构处理为柔性体，沿展向的所有剖面的翼型都是相同的，并假定每个翼型片条为刚体。水翼的弯曲和扭转变形分别采用两自由度水翼的沉浮和俯仰运动来模拟。对于非均直舵叶，一般取翼展方向70％-75％处的典型截面来建立二元颤振模型，通过二维模型来对弹性升力面建模。但是在这些学术论文中，几乎未提及如何获取水翼、控制面的纯弯、纯扭频率，以及如何将系统模型简化为二元颤振模型。因此，研究获取水翼纯弯、纯扭频率的方法具有一定意义。

舵系统的操纵系统部分往往由于长期工作磨损而产生间隙，这种间隙可能会引起结构持续发生微弱的、不衰减的振荡。这种现象并不会导致结构发生重大破坏，但会引起水噪声并降低水下航行器的隐蔽性。同时，舵叶严重的变形会使得结构呈现出明显的几何差异，位移和应变表现出非线性关系，即随着变形程度增大，刚度渐硬。传统线性颤振计算方法不能准确解决非线性系统的水动弹性问题。

多体系统传递矩阵法(mstmm)由芮筱亭院士及其团队建立，用于多体动力学分析；该方法能实现一般多体系统动力学研究，且该方法可以实现复杂系统的快速建模与快速计算，其高计算效率方便运用于工程中。

技术实现要素：

本发明的目的是提供一种二元翼型非线性颤振时域模型的建模方法，为舵系统非线性水弹性研究提供了一种有效的技术途径。

本发明的目的是这样实现的：一种二元翼型非线性颤振时域模型的建模方法，包括以下步骤：

步骤a、对系统进行简化，基于多体系统传递矩阵法推导弯扭耦合梁传递矩阵；

步骤b、确定各元件传递矩阵，拼装成总传递矩阵，建立系统多体动力学模型；

步骤c、令传递矩阵中刚心与质心重合，求解多体动力学模型，得到二元颤振模型的关键参数，即舵叶纯弯、纯扭频率；

步骤d、建立两元翼型非线性颤振时域分析模型；

步骤e、求解二元翼型非线性颤振模型，求得其时域响应，完成建模。

作为本发明的进一步限定，所述步骤a还包括：

根据舵叶的变形特性，将舵叶简化为多段不同参数的弯扭耦合梁，以舵叶弹性轴位置为x轴，以与扭簧相接的翼型弦线为z轴，以x轴、z轴交点为原点，y轴为经过原点垂直于xz平面的一条线，建立坐标系。

作为本发明的进一步限定，所述步骤a推导弯扭耦合梁传递矩阵具体包括：某段等截面舵叶的弯扭耦合梁模型中舵叶的长度为l，xα是质心到弹性轴的距离，质心在z轴正方向，则xα为正；以弯曲和扭转振动为主，忽略其剪切效应，推导舵叶弯扭耦合梁传递矩阵，建立弯扭耦合梁的振动微分方程：

式中，m为单位长度质量，iα为单位长度转动惯量，ei为弯曲刚度，gj为扭转刚度，x为舵叶轴向位移，y为舵叶弯曲方向位移，θx为扭转角度，t为时间，b为舵叶弦长的一半，xα质心到弹性轴的距离，且当质心在z正方向，xα为正；

由模态坐标转换，令

y(x,t)＝y(x)sinωt,θx(x,t)＝θx(x)sinωt(2)

式中，ω为圆频率；

将(2)带入(1)中，(1)式变为：

消去式(3)中的y(x)或者θx(x)，得到

式中，

w＝y或者θ(5)

引入无量纲长度

ξ＝x/l(6)

式(6)中l为划分后单元弯扭耦合梁长度；

式(4)可改写成无量纲形式

(d⁶+ad⁴-bd²-abc)w＝0(7)

其中，

六阶微分方程(7)的通解可以表示为：

w(ξ)＝c1coshαξ+c2sinhαξ+c3cosβξ+c4sinβξ+c5cosγξ+c6sinγξ(9)

式中c1-c6是常数，并且

q＝b+a²/3

式(9)中的w(ξ)代表弯曲位移y和扭转角度θx在不同常数下的解；因此，

y(ξ)＝a1coshαξ+a2sinhαξ+a3cosβξ+a4sinβξ+a5cosγξ+a6sinγξ(11)

θx(ξ)＝b1coshαξ+b2sinhαξ+b3cosβξ+b4sinβξ+b5cosγξ+b6sinγξ(12)

式中a1-a6和b1-b6是两组不同的常数；

将式(11)和(12)代入式(3)可以确定常数有如下规律：

式中，

从式(11)、(12)可以得到弯曲角度θz(ξ)，弯矩mz(ξ)，剪切力qy(ξ)和扭矩mx(ξ)的表达式：

因此可得

即z(ξ)＝b(ξ)·a,a＝[a1,a2,a3,a4,a5,a6]^t，其中z(ξ)为状态矢量，即方程(19)等式左边项，b(ξ)代表方程(19)等式右边的第一个矩阵；令ξ＝0，且根据方程(19)和多体系统传递矩阵法可将方程(19)写成zi＝b(0)·a形式；令ξ＝1得到zo＝b(1)·a＝b(1)b(0)^-1zi＝uizi；其中zo代表模态坐标下元件输出端的状态矢量，zi代表模态坐标下元件输入端的状态矢量；

得到弯扭耦合梁的传递矩阵为

ui＝b(1)·b^-1(0)(20)

其中，

作为本发明的进一步限定，所述步骤b具体包括：基于mstmm，状态矢量写为[x,y,θz,mz,qx,qy,θx,mx]^t，x为沿坐标轴x位移对应的模态坐标列阵，y为沿坐标轴y位移对应的模态坐标列阵，θz为该点处相对于平衡位置相对于在z轴的角位移对应的模态坐标列阵，mz为沿坐标轴z内力矩对应的模态坐标列阵，qx为沿坐标轴x内力对应的模态坐标列阵，qy为沿坐标轴y内力对应的模态坐标列阵，θx为该点处相对于平衡位置相对于x轴的角位移对应的模态坐标列阵，mx为沿坐标轴x内力矩对应的模态坐标列阵；

mstmm中，总传递矩阵设置如下：

zn,n+1＝uallz0,1(21)

式中uall＝un···u3u2u1，u1,u2,u3···un分别代表系统各元件的传递矩阵，zall＝[zn,n+1,···z1,2,z0,1]，z0,1,z1,2···zn,n+1分别代表系统各元件端点的状态矢量；

将扭簧定义为输入端，将离扭簧最远的弯扭耦合梁定义为输出端，扭簧到舵叶为传递方向；根据系统两端边界点，确定边界条件为；根据各段弯扭耦合梁参数确定其传递矩阵ui(i＝2,3,...,8)，根据扭簧具体参数确定其传递矩阵u1，建立系统总传递方程。

作为本发明的进一步限定，所述步骤c具体包括：将系统总传递方程中质心到弹性轴的距离都改为0(xα≈0)，得到和即将弯扭耦合梁中的耦合项去掉，求解修改过后的动力学模型：

求解式(22)即可得到舵叶纯弯、纯扭频率。

作为本发明的进一步限定，所述步骤d具体包括：考虑舵叶的间隙非线性和几何非线性，根据模型建立两自由度翼型运动控制方程：

式中，m为单位展长舵叶的质量；b为舵叶弦长的一半；为相对于弹性轴的单位展长转动惯量；rα是水翼对刚心的回转半径；ch和cα分别是沉浮和俯仰阻尼；α表示俯仰运动，h表示沉浮运动；lh为升力，取向上的方向为正方向；对弹性轴的水动力矩tα则以抬头为正；考虑间隙非线性和几何非线性的非线性项f(h)、g(h)分别表示回复力和回复力矩，f(h)、g(α)为位移h和α的函数，其表达式为：

式中，kh表示液压弹簧刚度系数，kα表示扭转刚度系数；非线性沉浮刚度系数，非线性俯仰刚度系数；ωh和ωα分别上一步骤中求出的纯弯、纯扭频率。

与现有技术相比，本发明所达到的有益效果：

(1)相比前人文献中均未给出二元翼型颤振模型中如何获得其纯弯、纯扭频率的方法，本发明提出基于多体系统传递矩阵法计算得到舵叶纯弯、纯扭频率的方法；

(2)本发明具有建模快速简单、计算速度快的特点，能快速计算出结果，解决了工程上仿真计算量过大、计算时间长的问题，为工程上类似的二元翼型颤振模型的快速建模与仿真提供参考；

(3)本发明在二元翼型颤振模型的建模中，同时考虑了间隙非线性和几何非线性，使颤振模型更接近实际，解决了传统线性颤振计算方法不能准确计算非线性系统的水动弹性问题。

附图说明

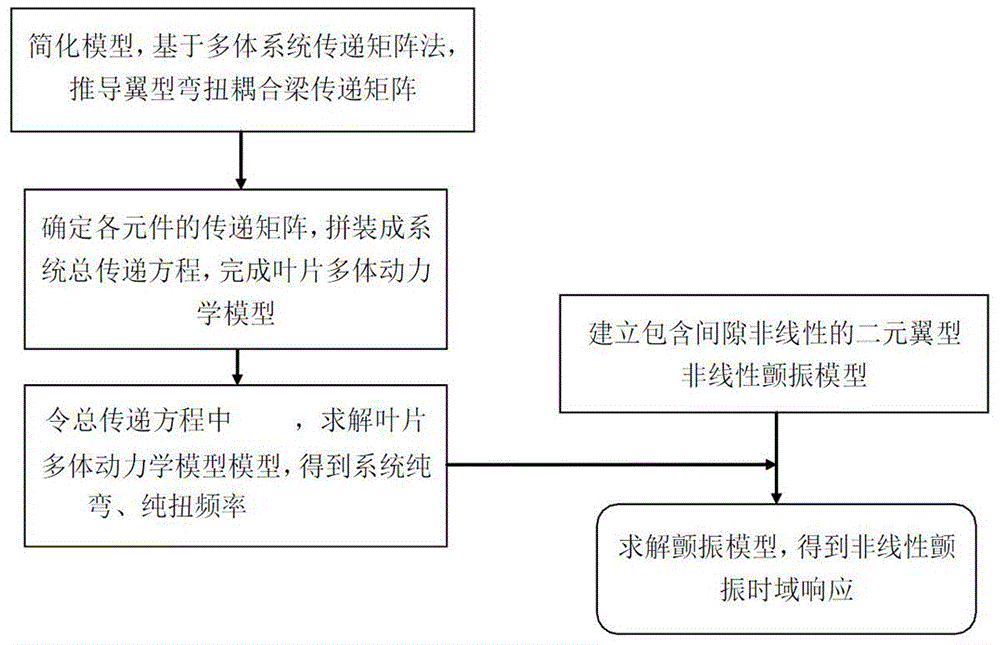
图1是本发明实例提供的一种二元翼型非线性颤振时域模型的建模流程示意图。

图2是舵叶模型简化示意图。

图3是弯扭耦合梁模型示意图。

图4是二元翼型非线性颤振模型示意图。

图5是二元翼型沉浮振幅随速度变化图。

图6是二元翼型俯仰振幅随速度变化图。

图7是当间隙为αs＝0.0065,ξs＝0.0005，来流速度为vnon＝0.01的相轨图。

图8是当间隙为αs＝0.0065,ξs＝0.0005，来流速度为vnon＝0.01的频谱分析图。

图9是来流速度下响应频率的分布图。

具体实施方式

下面结合附图对本发明作进一步描述；以下实施例仅用于更加清楚地说明本发明的技术方案，而不能以此来限制本发明的保护范围。

本发明的一种二元翼型非线性颤振时域模型的建模方法，参见图1所示。现以某水下舵叶为例，根据一根扭簧连接一个舵叶的系统建立二元翼型非线性颤振模型，进行时域颤振分析。系统结构如图2所示。

系统具体参数如下：扭簧刚度为kα＝1.23×10⁷n·m/rad，质心到弹性轴的距离xα＝0.2889，水翼对刚心的回转半径rα²＝0.405，舵叶弦长的一半b＝0.9m，质量比μ＝0.403，刚心距离弦线中点的距离与半弦长的比值a＝-0.48，沉浮间隙无量纲量ξs＝0～0.0005，俯仰间隙无量纲量as＝0～0.0065rad。

具体实施步骤如下：

步骤一：对系统进行简化，基于多体系统传递矩阵法推导弯扭耦合梁传递矩阵。

根据舵叶的变形特性，将舵叶简化为7段不同参数的弯扭耦合梁，如图2所示，以舵叶弹性轴位置为x轴，以与扭簧相接的翼型弦线为z轴，以x轴、z轴交点为原点，y轴为经过原点垂直于xz平面的一条线，建立坐标系。如图3所示为某段等截面舵叶的弯扭耦合梁模型，该段舵叶的长度为l，xα是质心到弹性轴的距离，质心在z轴正方向，则xα为正。

舵叶主要以弯曲和扭转振动为主，忽略其剪切效应，推导舵叶弯扭耦合梁传递矩阵，建立弯扭耦合梁的振动微分方程：

式中，m为单位长度质量，iα为单位长度转动惯量，ei为弯曲刚度，gj为扭转刚度，x为舵叶轴向位移，y为舵叶弯曲方向位移，θx为扭转角度，t为时间，b为舵叶弦长的一半，xα质心到弹性轴的距离，且当质心在z正方向，xα为正；

由模态坐标转换，令

y(x,t)＝y(x)sinωt,θx(x,t)＝θx(x)sinωt(2)

式中，ω为圆频率；

将(2)带入(1)中，(1)式变为：

消去式(3)中的y(x)或者θx(x)，得到

式中，

w＝y或者θ(5)

引入无量纲长度

ξ＝x/l(6)

式(6)中l为划分后单元弯扭耦合梁长度；

式(4)可改写成无量纲形式

(d⁶+ad⁴-bd²-abc)w＝0(7)

其中，

六阶微分方程(7)的通解可以表示为

w(ξ)＝c1coshαξ+c2sinhαξ+c3cosβξ+c4sinβξ+c5cosγξ+c6sinγξ(9)

式中c1-c6是常数，并且

q＝b+a²/3

式(9)中的w(ξ)代表弯曲位移y和扭转角度θx在不同常数下的解；因此，

y(ξ)＝a1coshαξ+a2sinhαξ+a3cosβξ+a4sinβξ+a5cosγξ+a6sinγξ(11)

θx(ξ)＝b1coshαξ+b2sinhαξ+b3cosβξ+b4sinβξ+b5cosγξ+b6sinγξ(12)

式中a1-a6和b1-b6是两组不同的常数；

将式(11)和(12)代入式(3)可以确定常数有如下规律：

式中，

从式(11)、(12)可以得到弯曲角度θz(ξ)，弯矩mz(ξ)，剪切力qy(ξ)和扭矩mx(ξ)的表达式：

因此可得

即z(ξ)＝b(ξ)·a,a＝[a1,a2,a3,a4,a5,a6]^t，其中z(ξ)为状态矢量，即方程(19)等式左边项，b(ξ)代表方程(19)等式右边的第一个矩阵；令ξ＝0，且根据方程(19)和多体系统传递矩阵法可将方程(19)写成zi＝b(0)·a形式；令ξ＝1得到zo＝b(1)·a＝b(1)b(0)^-1zi＝uizi；其中zo代表模态坐标下元件输出端的状态矢量，zi代表模态坐标下元件输入端的状态矢量；

所以弯扭耦合梁的传递矩阵为

ui＝b(1)·b^-1(0)(20)

其中，

步骤二：确定各元件传递矩阵，拼装成总传递矩阵，建立系统多体动力学模型；

基于mstmm，状态矢量写为[x,y,θz,mz,qx,qy,θx,mx]^t，x为沿坐标轴x位移对应的模态坐标列阵，y为沿坐标轴y位移对应的模态坐标列阵，θz为该点处相对于平衡位置相对于在z轴的角位移对应的模态坐标列阵，mz为沿坐标轴z内力矩对应的模态坐标列阵，qx为沿坐标轴x内力对应的模态坐标列阵，qy为沿坐标轴y内力对应的模态坐标列阵，θx为该点处相对于平衡位置相对于x轴的角位移对应的模态坐标列阵，mx为沿坐标轴x内力矩对应的模态坐标列阵；

mstmm中，总传递矩阵设置如下：

zn,n+1＝uallz0,1(21)

式中uall＝un···u3u2u1，u1,u2,u3···un分别代表系统各元件的传递矩阵，zall＝[zn,n+1,···z1,2,z0,1]，z0,1,z1,2···zn,n+1分别代表系统各元件端点的状态矢量；

将扭簧定义为输入端，将离扭簧最远的弯扭耦合梁定义为输出端，扭簧到舵叶为传递方向。根据系统两端边界点，确定边界条件为：输入端z1,0＝[0,0,0,mz1,qx1,qy1,0,mx1]^t，输出端z9,0＝[x9,y9,θz9,0,0,0,θx9,0]^t。z1,0为模态坐标下系统输入端的状态矢量，z9,0为模态坐标下系统输出端的状态矢量，

根据各段弯扭耦合梁参数确定其传递矩阵ui(i＝2,3,...,8)，根据扭簧具体参数确定其传递矩阵u1，建立系统总传递方程为：

步骤三：令传递矩阵中刚心与质心重合，求解多体动力学模型，得到二元颤振模型的关键参数，即舵叶纯弯、纯扭频率；

将系统总传递方程中质心到弹性轴的距离都改为0(xα≈0)，得到和即将弯扭耦合梁中的耦合项去掉，求解修改过后的动力学模型，即可得到舵叶纯弯、纯扭频率。

具体求解方法如下：

将边界条件代入舵系统总传递方程可得到系统特征方程：

式中为去掉零元素后得到的矩阵，为消去中与中零元素对应列得到的方阵；

由于和uall都只与系统的结构参数和固有频率有关，对于实际的线性振动系统，式(23)必有非零解，所以

求解式(24)即可求出舵叶的纯弯频率ωh、纯扭频率ωα。

步骤四：建立两元翼型非线性颤振时域分析模型；

取3/4叶片展长处的截面，考虑间隙非线性和几何非线性，建立二元水翼模型，如图4所示。在水翼弹性轴处固定一根刚度为kh弹簧以及一根刚度为kα的扭簧，弹性轴在翼弦中点前ab处，质心到弹性轴的距离为xαb，水翼弦长为2b。水翼有两个自由度，即随弹性轴的沉浮运动h(向下为正)和绕弹性轴的俯仰转动α(抬头为正)；图4中，hs是沉浮间隙，αs是俯仰间隙。

根据模型建立两自由度翼型运动控制方程：

式中，m为单位展长舵叶的质量；b为舵叶弦长的一半；为相对于弹性轴的单位展长转动惯量；rα是水翼对刚心的回转半径；ch和cα分别是沉浮和俯仰阻尼；α表示俯仰运动，h表示沉浮运动；lh(t)为升力，取向上的方向为正方向；对弹性轴的水动力矩tα(t)则以抬头为正。考虑间隙非线性和几何非线性的非线性项f(h)、g(h)分别表示回复力和回复力矩，f(h)、g(α)为位移h和α的函数，其表达式为：

式中，kh表示液压弹簧刚度系数，kα表示扭转刚度系数；非线性沉浮刚度系数，非线性俯仰刚度系数。

根据theodorsen非定常任意水动力流体理论，在不可压缩流中的二元水翼，水翼单位展长的升力lh(t)(向上为正)和对刚心的俯仰力矩tα(t)(迎风抬头为正)分别为：

式中，ρ为不可压缩流体的密度，σ为表征时间的量，为无量纲时间，a为刚心距离弦线中点的距离与半弦长的比值，并在中点后为正；

为了方便推导非线性颤振方程，将升力和力矩整理为如下简洁形式：

式中，

步骤五：求解二元翼型非线性颤振模型，求得其时域响应；

由于式(31)中存在积分项，引入新的状态变化量如下：

根据式(25)、(26)、(27)、(30)、(31)和式(32)可以推导出状态空间中两自由度二元非线性水翼无量纲形式的水弹性方程为

式中，

其中，

式中，ωh和ωα分别上一步骤中求出的无耦合沉浮和俯仰固有频率，为频率比，为翼型绕弹性轴的无量纲回转半径，xα为翼型质量中心到弹性轴的无量纲距离，ξξ和ξα分别为沉浮和俯仰运动的阻尼比，μ为质量比，u为来流速度，vnon为无量纲来流速度，为无量纲时间，rξ为非线性沉浮刚度系数无量纲量，rα是非线性俯仰刚度系数无量纲量，ξs是沉浮间隙无量纲量，αs是俯仰间隙无量纲量。

采用龙格库塔法求解式(33)及给定初始条件ξ(0)＝0，α(0)＝0.01rad(一般给α一个较小的初值)可以得到二元水翼的时域响应。

沉浮和俯仰振幅随着vnon变化图如图5和6所示；从图中可以看出，当俯仰间隙和沉浮间隙的值为αs＝0.0065,ξs＝0.0005时，vnon＜0.07舵系统发生极限循环振动(lco)现象，这种持续的振动可能诱发水噪声，降低水下航行器的隐蔽性。当vnon＞0.07时，系统只是发生了静变形，可能会降低舵面的操纵效率。在vnon≈0.08左右时，系统的静变形发生跳跃现象。因此，系统在包含间隙非线性的情况下，可能发生lco和静变形等现象。

从图7可以看出，当间隙为αs＝0.0065,ξs＝0.0005，来流速度为vnon＝0.01，舵系统发生了lco现象，对应的频谱分析图如图8所示，在频率为10.09hz左右有一个离散峰，离散峰处的能量相比其它处要高，表明此处容易激发出水噪声。

对图5、6工况下计算出的响应做频谱分析，获得响应频率，绘制出不同来流速度下响应频率的分布图，如图9所示。从图中可以看出，随着速度的增加，系统的响应频率逐渐降低。

同样，本方法对不同叶片建立二元翼型非线性颤振模型，只需修改简化模型和系统中具体参数即可。

本发明并不局限于上述实施例，在本发明公开的技术方案的基础上，本领域的技术人员根据所公开的技术内容，不需要创造性的劳动就可以对其中的一些技术特征作出一些替换和变形，这些替换和变形均在本发明的保护范围内。