多视图相机位姿和场景的纯位姿解算方法及系统与流程

本发明涉及计算机视觉领域，具体地，涉及一种多视图相机位姿和场景的纯位姿解算方法及系统。

背景技术：

一直以来，相机位姿与场景结构的恢复是计算机视觉中运动恢复结构的核心部分。在传统的多视图几何描述下，相机位姿和场景结构的恢复需要进行全局参数的初始化和集束调整(bundleadjustment，ba)。一方面，全局参数初始化的目的是为ba集束调整优化提供初值，主要分为全局姿态、全局位移和三维场景点坐标的初始化，其中难点在于全局位移的初始化方面。传统的全局位移方法一般以双视图相对位移为输入，通过代数误差最小来优化全局位移，在相机纯旋转或共线运动等情况下会出现异常。另一方面，ba集束调整优化以重投影误差最小为优化目标，参数空间包括三维场景点坐标、位姿参数及相机参数等。对于m个三维场景点和n幅图像的情形，优化参数的空间维数为3m+6n。由于三维场景点的数目通常很大，造成待优化的参数空间维数巨大。

专利文献cn106408653a公开了一种面向大规模三维重建的实时鲁棒的集束调整方法，目前集束调整的主流方法是考虑参数雅克比(jacobian)矩阵稀疏性的非线性优化算法，但在大尺度场景下仍然不能满足实时及鲁棒性需求。

技术实现要素：

针对现有技术中的缺陷，本发明的目的是提供一种多视图相机位姿和场景的纯位姿解算方法及系统。

根据本发明提供的一种多视图相机位姿和场景的纯位姿解算方法，以视图姿态初值为输入，包括：

纯旋转异常识别(purerotationrecoginition,prr)步骤：对所有视图进行纯旋转异常识别，对纯旋转异常的视图进行标记，得到标记视图和非标记视图；

全局位移线性计算(globaltranslationlinear，gtl)步骤：从非标记视图中选择一幅作为参考视图，构建约束tr＝0，构建全局位移线性约束，求解全局位移根据tr和恢复标记视图的全局位移，并筛选全局位移的正确解；

三维场景解析恢复(structureanalyticalreconstruction,sar)步骤：根据全局位姿的正确解，解析恢复所有3d点的坐标。

优选地，所述prr纯旋转异常识别步骤包括：

步骤1：考虑视图i，1≤i≤n，对于视图j∈vi，利用双视图(i,j)上的所有图像匹配点对(xi,xj)以及相对姿态ri,j，计算θi,j＝||[xj]×ri,jxi||，并构成集合θi,j和记集合θi中大于δ1的比例为γi。

步骤2：若γi＜δ2，标记视图i为纯旋转异常视图，记θi,j集合中元素的均值为取构建约束ti＝tl；

其中，若3d点x^w＝(x^w,y^w,z^w)^t在n(≤n)幅视图中可视，对于i＝1,2,…,n,vi为所有与视图i共视的视图构成的集合，xi和xj分别表示点x^w在视图i和视图j上的归一化图像坐标，δ1和δ2为设定的阈值，ri和ti分别表示视图i的全局姿态和全局位移，和ti,j分别表示双视图(i,j)的相对姿态和相对位移，[xj]x表示由向量xj构成的反对称矩阵；

步骤3：对所有视图重复步骤1-步骤2。

优选地，所述gtl全局位移计算步骤包括：

步骤1：对于当前3d点，选择视图其中视图为左基准视图，η为右基准视图；

步骤2：对于所有的非标记视图(不含参考视图)，按照形如构建gtl全局位移线性约束。

3d点x^w在视图i上的图像归一化坐标有其中～表示齐次坐标下的等式，其中上标t表示矩阵或向量的转置。为了线性求解全局位移，可以定义不同的目标函数形式，典型如和[xi]×yi＝0，其中i3表示三维单位矩阵，e3表示单位矩阵的第三列向量e3＝(0,0,1)^t。另外，由于相对位移ti,j关于全局位移具有不同形式，典型如ti,j＝rj(ti-tj)和ti,j＝tj-ri,jti，因此矩阵b、c和d也相应地具有不同形式：

(1)对于目标函数[xi]×yi＝0和相对位移ti,j＝rj(ti-tj)，d＝-(b+c)；

(2)对于目标函数和相对位移ti,j＝rj(ti-tj)，d＝-(b+c)；

(3)对于目标函数[xi]×yi＝0和相对位移ti,j＝tj-ri,jti，

(4)对于目标函数和相对位移ti,j＝tj-ri,jti，

步骤3：对于其它3d点，重复步骤1-步骤2，构建线性方程，求解全局位移

步骤4：利用和tr，根据ti＝tl恢复标记视图的全局位移；

步骤5：根据筛选全局位移t的正确解。

优选地，在所述gtl全局位移计算步骤与所述sar三维场景解析恢复步骤之间还增添一个可选的相机位姿优化步骤：

3d点x^w在视图i上的图像齐次坐标fi表示为

其中～表示齐次坐标下的等式，定义重投影误差为

其中为3d点在视图i上的图像坐标且第三元素为1，对于该3d点的所有视图，构成重投影误差向量ε，对于所有3d点，构成误差向量∑，全局位姿优化的目标函数描述为argminσ^tσ，据此进行全局位姿的优化求解。需要指出的是，此处的相机位姿优化步骤可以替换为其他优化算法，如经典ba集束调整算法，此时三维场景点坐标既可以使用经典ba集束调整算法的输出结果，也可以利用如下的sar三维场景解析恢复步骤得到。

优选地，所述sar三维场景解析恢复步骤包括：

多视图下三维场景结构通过相机位姿进行解析加权重建。

对于当前3d点，在左基准视图中的景深计算为

在右基准视图中的景深计算为

其中和ωj,,η表示加权系数。以左基准视图景深解析恢复3d点为例，可取则当前3d特征点坐标为

据此可解析恢复出所有3d点的坐标。同理，可以利用右视图景深解析恢复3d点坐标。当然，也可以取以上两种3d点坐标的算数平均。

根据本发明提供的一种多视图相机位姿和场景的纯位姿解算系统，包括：

纯旋转异常识别模块：对所有视图进行纯旋转异常识别，对纯旋转异常的视图进行标记，得到标记视图和非标记视图；

全局位移恢复模块：从非标记视图中选择一幅作为参考，构建约束tr＝0，构建全局位移线性约束，求解全局位移根据tr和恢复标记视图的全局位移，并筛选全局位移的正确解；

三维场景恢复模块：根据全局位姿的正确解，解析恢复所有3d点的坐标。

优选地，所述纯旋转异常识别模块包括：

模块m11：考虑视图i，1≤i≤n，对于视图j∈vi，利用双视图(i,j)上的所有图像匹配点对(xi,xj)以及相对姿态ri,j，计算θi,j＝||[xj]×ri,jxi||，并构成集合θi,j和记集合θi中大于δ1的比例为γi；

模块m12：若γi＜δ2，标记视图i为纯旋转异常视图，记θi,j集合中元素的均值为取构建约束ti＝tl；

其中，若3d点x^w＝(x^w,y^w,z^w)^t在n(≤n)幅视图中可视，对于i＝1,2,…,n,vi为所有与视图i共视的视图构成的集合，xi和xj分别表示点x^w在视图i和视图j上的归一化图像坐标，δ1和δ2为设定的阈值，ri和ti分别表示视图i的全局姿态和全局位移，和ti,j分别表示双视图(i,j)的相对姿态和相对位移，[xj]×表示由向量xj构成的反对称矩阵；

模块m13：对所有视图重复模块m11-模块m12的操作。

优选地，所述全局位移恢复模块包括：

模块m21：对于当前3d点，选择视图其中视图为左基准视图，η为右基准视图；

模块m22：对于所有的非标记视图，按照形如构建gtl全局位移线性约束；

3d点x^w在视图i上的图像归一化坐标有其中～表示齐次坐标下的等式，其中上标t表示矩阵或向量的转置；

另外，由于相对位移ti,j关于全局位移具有不同形式，因此矩阵b、c和d也相应地具有不同形式：

(1)对于目标函数[xi]×yi＝0和相对位移ti,j＝rj(ti-tj)，d＝-(b+c)；

(2)对于目标函数和相对位移ti,j＝rj(ti-tj)，d＝-(b+c)；

(3)对于目标函数[xi]×yi＝0和相对位移ti,j＝tj-ri,jti，

(4)对于目标函数和相对位移ti,j＝tj-ri,jti，

模块m23：对于其它3d点，重复模块m21-模块m22的操作，构建线性方程，求解全局位移

模块m24：利用和tr，根据ti＝tl恢复标记视图的全局位移；

模块m25：根据筛选全局位移t的正确解。

优选地，还包括相机位姿优化模块：

3d点x^w在视图i上的图像齐次坐标fi表示为

其中～表示齐次坐标下的等式，定义重投影误差为

其中为3d点在视图i上的图像坐标且第三元素为1，对于该3d点的所有视图，构成重投影误差向量ε，对于所有3d点，构成误差向量∑，全局位姿优化的目标函数描述为argmin∑^t∑，据此进行全局位姿的优化求解；

或者，将所述相机位姿优化步骤替换为经典ba集束调整算法，此时三维场景点坐标既使用经典ba集束调整算法的输出结果，或利用sar三维场景解析恢复步骤得到。

优选地，所述三维场景恢复模块包括：

多视图下三维场景结构通过相机位姿进行解析加权重建；

对于当前3d点，在左基准视图中的景深计算为

在右基准视图中的景深计算为

其中和ωj,，η表示加权系数；

据此解析恢复出所有3d点的坐标，或利用右视图景深解析恢复3d点坐标，或取以上两种3d点坐标的算数平均。

与现有技术相比，本发明具有如下的有益效果：

本发明突破传统初值和优化方法的瓶颈，可大幅度提升相机位姿与场景结构恢复的鲁棒性及计算速度。

附图说明

通过阅读参照以下附图对非限制性实施例所作的详细描述，本发明的其它特征、目的和优点将会变得更明显：

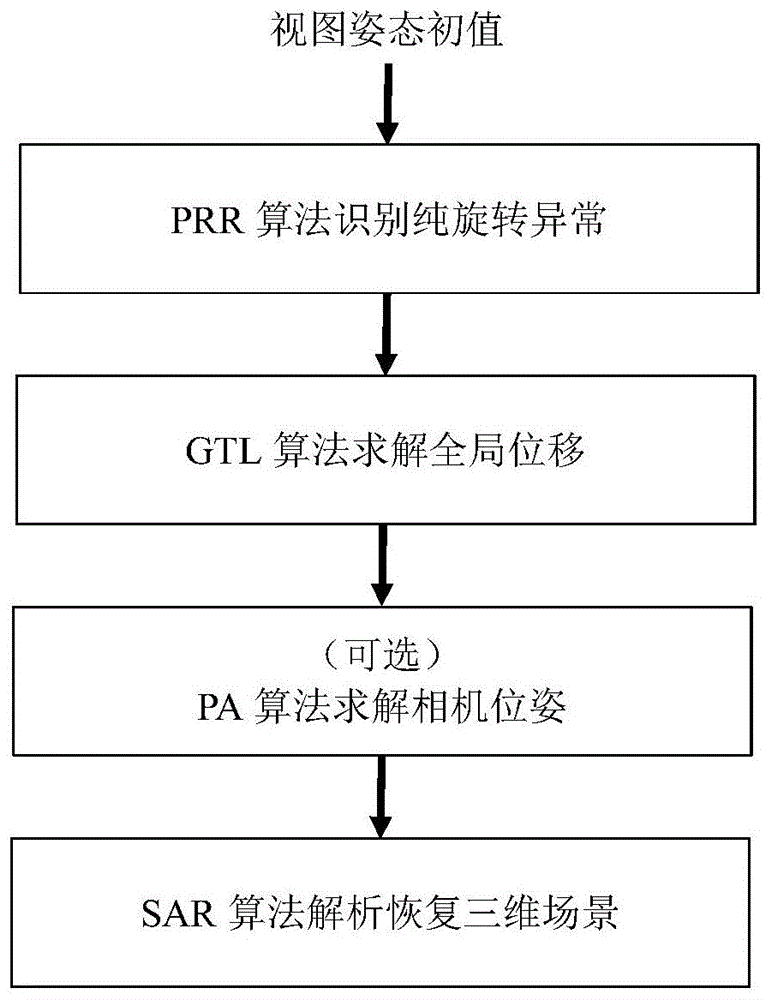
图1为本发明的工作流程图。

具体实施方式

下面结合具体实施例对本发明进行详细说明。以下实施例将有助于本领域的技术人员进一步理解本发明，但不以任何形式限制本发明。应当指出的是，对本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变化和改进。这些都属于本发明的保护范围。

如图1所示，本发明提供的一种多视图相机位姿和场景的纯位姿解算方法，以视图姿态初值为输入，包括：

纯旋转异常识别(purerotationrecoginition,prr)步骤：对所有视图进行纯旋转异常识别，对纯旋转异常的视图进行标记，得到标记视图和非标记视图；

全局位移线性计算(globaltranslationlinear，gtl)步骤：从非标记视图中选择一幅作为参考视图，构建约束tr＝0，构建全局位移线性约束，求解全局位移根据tr和恢复标记视图的全局位移，并筛选全局位移的正确解；

三维场景解析恢复(structureanalyticalreconstruction,sar)步骤：根据全局位姿的正确解，解析恢复所有3d点的坐标。

prr纯旋转异常识别步骤包括：

步骤1：考虑视图i，1≤i≤n，对于视图j∈vi，利用双视图(i,j)上的所有图像匹配点对(xi,xj)以及相对姿态ri,j，计算θi,j＝||[xj]×ri,jxi||，并构成集合θi,j和记集合θi中大于δ1的比例为γi。

步骤2：若γi＜δ2，标记视图i为纯旋转异常视图，记θi,j集合中元素的均值为取构建约束ti＝tl；

其中，若3d点x^w＝(x^w,y^w,z^w)^t在n(≤n)幅视图中可视，对于i＝1,2,…,n,vi为所有与视图i共视的视图构成的集合，xi和xj分别表示点x^w在视图i和视图j上的归一化图像坐标，δ1和δ2为设定的阈值，ri和ti分别表示视图i的全局姿态和全局位移，和ti,j分别表示双视图(i,j)的相对姿态和相对位移，[xj]×表示由向量xj构成的反对称矩阵；

步骤3：对所有视图重复步骤1-步骤2。

gtl全局位移计算步骤包括：

步骤1：对于当前3d点，选择视图其中视图ζ为左基准视图，η为右基准视图；

步骤2：对于所有的非标记视图(不含参考视图)，按照形如构建gtl全局位移线性约束。

3d点x^w在视图i上的图像归一化坐标有其中～表示齐次坐标下的等式，其中上标t表示矩阵或向量的转置。为了线性求解全局位移，可以定义不同的目标函数形式，典型如和[xi]×yi＝0，其中i3表示三维单位矩阵，e3表示单位矩阵的第三列向量e3＝(0,0,1)^t。另外，由于相对位移ti,j关于全局位移具有不同形式，典型如ti,j＝rj(ti-tj)和ti,j＝tj-ri,jti，因此矩阵b、c和d的也相应地具有不同形式：

(1)对于目标函数[xi]×yi＝0和相对位移ti,j＝rj(ti-tj)，d＝-(b+c)；

(2)对于目标函数和相对位移ti,j＝rj(ti-tj)，d＝-(b+c)；

(3)对于目标函数[xi]×yi＝0和相对位移ti,j＝tj-ri,jti，

(4)对于目标函数和相对位移ti,j＝tj-ri,jti，

步骤3：对于其它3d点，重复步骤1-步骤2，构建线性方程，求解全局位移

步骤4：利用和tr，根据ti＝tl恢复标记视图的全局位移；

步骤5：根据筛选全局位移t的正确解。

在gtl全局位移计算步骤与所述sar三维场景解析恢复步骤之间还增添一个可选的相机位姿优化步骤：

3d点x^w在视图i上的图像齐次坐标fi表示为

其中～表示齐次坐标下的等式，定义重投影误差为

其中为3d点在视图i上的图像坐标且第三元素为1，对于该3d点的所有视图，构成重投影误差向量ε，对于所有3d点，构成误差向量∑，全局位姿优化的目标函数描述为argmin∑^t∑，据此进行全局位姿的优化求解。需要指出的是，此处的相机位姿优化步骤可以替换为其他优化算法，如经典ba集束调整算法，此时三维场景点坐标既可以使用经典ba集束调整算法的输出结果，也可以利用sar三维场景解析恢复步骤得到。

sar三维场景解析恢复步骤包括：

多视图下三维场景结构通过相机位姿进行解析加权重建。

对于当前3d点，在左基准视图中的景深计算为

在右基准视图中的景深计算为

其中和ωj,，η表示加权系数。以左基准视图景深解析恢复3d点为例，可取则当前3d特征点坐标为

据此可解析恢复出所有3d点的坐标。同理，可以利用右视图景深解析恢复3d点坐标。当然，也可以取以上两种3d点坐标的算数平均。

在上述一种多视图相机位姿和场景的纯位姿解算方法的基础上，本发明还提供一种多视图相机位姿和场景的纯位姿解算系统，包括：

纯旋转异常识别模块：对所有视图进行纯旋转异常识别，对纯旋转异常的视图进行标记，得到标记视图和非标记视图；

全局位移恢复模块：从非标记视图中选择一幅作为参考，构建约束tr＝0，构建全局位移线性约束，求解全局位移根据tr和恢复标记视图的全局位移，并筛选全局位移的正确解；

三维场景恢复模块：根据全局位姿的正确解，解析恢复所有3d点的坐标。

本领域技术人员知道，除了以纯计算机可读程序代码方式实现本发明提供的系统及其各个装置、模块、单元以外，完全可以通过将方法步骤进行逻辑编程来使得本发明提供的系统及其各个装置、模块、单元以逻辑门、开关、专用集成电路、可编程逻辑控制器以及嵌入式微控制器等的形式来实现相同功能。所以，本发明提供的系统及其各项装置、模块、单元可以被认为是一种硬件部件，而对其内包括的用于实现各种功能的装置、模块、单元也可以视为硬件部件内的结构；也可以将用于实现各种功能的装置、模块、单元视为既可以是实现方法的软件模块又可以是硬件部件内的结构。

以上对本发明的具体实施例进行了描述。需要理解的是，本发明并不局限于上述特定实施方式，本领域技术人员可以在权利要求的范围内做出各种变化或修改，这并不影响本发明的实质内容。在不冲突的情况下，本申请的实施例和实施例中的特征可以任意相互组合。