考虑混合不确定性的颗粒增强材料构件稳健拓扑优化方法与流程

本发明属于装备结构优化设计领域，涉及一种考虑混合不确定性的颗粒增强材料构件稳健拓扑优化方法。

背景技术：

拓扑优化作为一种调配有限材料在结构设计域内的分布、以使结构具有最优目标性能的方法，已广泛应用于结构设计中，并随着近年来增材制造技术的推广而进一步成熟。由于生产制造与使用过程中存在各种不确定性，为使拓扑优化设计结果经过实际加工后不至于性能劣化，考虑不确定性的稳健拓扑优化也已获得丰富成果。但是，目前结构拓扑稳健优化方法绝大多仅考虑单纯概率或单纯区间不确定性，考虑概率区间混合不确定性的结构稳健拓扑优化没有得到广泛深入的研究，主要体现在：

1)概率不确定性的建模方式会影响目标性能的分析精度，进而影响稳健拓扑优化结果。现有采用正态分布描述概率不确定性的手段在工程中存在不合理性，即：正态分布参数在理论上可取负值与正无穷，这与实际工程中不确定性参数仅在某一范围内概率性波动的事实不符。2)概率区间混合不确定性同时存在时的目标性能估计方式理论支撑薄弱，现有考虑概率区间混合不确定性的结构稳健拓扑优化方法仅能给出目标性能统计矩的上界(最差性能)，但无法给出对应的最差工况(特别是在不确定性外载作为区间不确定性变量时)——最差工况这在工程实际分析中往往具有重要指导作用。3)现有考虑概率区间混合不确定性的结构稳健拓扑优化方法均仅针对使用单一材料的问题进行了研究，对于使用多相材料、功能梯度材料等广义复合材料的结构稳健拓扑优化缺少关注。事实上，增材制造中选择性激光烧结或熔融等手段目前已可以成熟应用于具有复杂拓扑结构的金属、陶瓷材料或各类复合增强材料，且结构中材料的构成可以得到较精准的控制，因此对于使用复合材料的结构稳健拓扑优化具有实际研究价值与现实需要。

另一方面，现有针对广义复合材料的结构稳健拓扑优化方法在实际应用方面存在一定缺陷。目前的方法研究趋势是利用微观可变晶格结构来实现宏观结构上同一材料、不同等效物理属性的梯度性质。但受制于现有增材制造技术水平，实际结构性能往往存在劣化，其原因在于：1)晶格中的微小拓扑结构可能不能完整复现，特别是如五模超材料中理论无穷小的微刚性杆结点；2)增材制造过程中不可避免制造误差，而在晶格结构的微观层面引入几何边界不确定性从而进行结构稳健拓扑优化的工作路线存在一定困难，其部分原因是计算代价与目标函数梯度信息的获得。因此不考虑微观结构的单一尺度复合材料(如目前广泛应用的碳纤维增强塑料、颗粒增强金属/金属陶瓷材料等)在今后较长时间内仍会是适合实际制造生产的材料形式，对于该类材料的结构稳健拓扑优化具有特别迫切的研究需要。

技术实现要素：

为解决概率区间不确定因素共存情况下、使用颗粒增强材料构件的稳健拓扑优化设计问题，本发明提供了考虑区间与有界概率混合不确定性的颗粒增强材料构件稳健拓扑优化设计方法。考虑基于颗粒增强材料的构件在制造与使用过程中的不确定性，将其中样本不充分的外载视为区间不确定性、将样本充足的构件基体属性与颗粒增强相在基体中的体积分布视为有界概率不确定性；分别对设计域、颗粒增强相在构件基体中的体积分布进行离散化，设置结构约束、外载，建立考虑区间与有界概率混合不确定性的颗粒增强材料构件稳健优化设计模型；使用最优准则法迭代求解该模型：首先解耦概率区间混合不确定性，利用优化目标梯度信息确定最差工况；接着使用单变量降维方法与拉盖尔(laguerre)积分格式估计最差工况下优化目标的均值、方差以构造目标函数；最后分别计算目标函数与约束函数的梯度以更新设计变量。从而，高效地解决了概率区间不确定因素共存情况下、使用颗粒增强材料构件的稳健拓扑优化设计问题。

本发明是通过以下技术方案实现的：一种考虑混合不确定性的颗粒增强材料构件稳健拓扑优化方法，该方法包括以下步骤：

1)考虑基于颗粒增强材料的构件在制造与使用过程中的以下不确定性：构件基体材料的材料属性、颗粒增强相的材料属性、颗粒增强相在基体中分布的体积分数、构件所受外载的幅值与方向；其中，由于难以获得关于外载的充足样本信息，故将外载的幅值与方向不确定性视为区间不确定性处理；将具有充足样本信息的基体材料材料属性、颗粒增强相材料属性、颗粒增强相在基体中分布的体积分数视为有界概率不确定性处理，并采用服从广义贝塔分布(gbeta分布)的随机变量来描述各有界概率不确定性参数；

2)对构件设计域进行离散化，具体为：

简化构件受力情况为二维平面应力状态，保留构件孔洞(如铰接孔等)、同时去除细节几何形状(如倒角、圆角等)以提高计算效率；将化简的构件置于一规则矩形设计域内，并将该矩形设计域划分为nx×ny个正方形单元，其中nx，ny分别为沿x,y轴方向的划分数；基于拓扑优化中经典的带罚各向同性材料(smip)框架，每一单元赋予唯一设计变量ρe∈[0,1](e＝1,2,…,nxny)；

3)对颗粒增强相在构件基体中的体积分布进行离散化，具体为：

3.1)根据离散设计域指定坐标系，以构件传力方向为x轴，则各单元坐标可唯一确定；颗粒增强材料构件中，颗粒增强相在基体中的体积分数为分层渐变，即颗粒增强相在基体中的体积分数仅沿垂直于构件传力方向(即y轴方向)发生变化，记该理论变化方式为vol(y)，是坐标y的连续函数，根据构件实际使用要求进行选择，同一厚度上颗粒增强相的体积分数为常数；考虑该颗粒增强相体积分数在实际生产中的不确定性波动，记实际变化方式为vol^*(y)，具有有界概率不确定性；

3.2)根据已离散的构件设计域与颗粒增强相体积分数变化方式，计算第i(i＝1,2,…,ny)层内、颗粒增强相的平均体积分数vol^*(i)；i层内全部单元的颗粒增强相体积分数均为vol^*(i)，是层号i的离散函数；

3.3)使用halpin-tsai微观结构模型，计算第i(i＝1,2,…,ny)层内各单元杨氏模量与泊松比

3.4)基于拓扑优化中经典的带罚各向同性材料(smip)框架，引入罚因子，则第i(i＝1,2,…,ny)层内各单元的杨氏模量最终可表达为：

式eq.1中，emin分别为3.3)计算得到的第i(i＝1,2,…,ny)层内各单元杨氏模量、事先指定的最小杨氏模量允许值，为常数；p是事先指定的常数罚因子；为基于带罚各向同性材料(smip)框架构造的第i(i＝1,2,…,ny)层内各单元的杨氏模量；

4)对已离散化的结构施加物理约束与几何约束，具体为：

4.1)物理约束包括结构的固定或支持、外部载荷，依据经典有限元方式施加；

4.2)几何约束包括结构中指定的孔洞与强制保留材料的区域，其方法是对于孔洞覆盖的单元所对应的设计变量置ρe≡0而要求强制保留材料位置覆盖的单元所对应的设计变量置ρe≡1，并在后续优化过程中不改变其数值；

5)颗粒增强材料构件的结构屈服是优化设计目标，在稳健拓扑优化框架内考虑区间与有界概率混合不确定性共同影响下的结构屈服，故可将构件在最差工况下的屈服均值与标准差作为优化设计目标的表征，建立考虑区间与有界概率混合不确定性的颗粒增强材料构件稳健优化设计模型如eq.2所示：

式eq.2中，是(nxny)×1维设计向量，ρmin是设计中给定的各设计变量最小允许值，为常数；x＝(x1,x2,…,xm)^t是m×1维有界概率不确定性向量，其元素包括构件基体材料的材料属性、颗粒增强相材料属性、颗粒增强相在基体材料中体积分布的不确定度；i＝(f1,f2,…,fn,α1,α2,…,αn)^t是2n×1维区间不确定性向量，其中f1,f2,…,fn分别为构件所受n个不确定外载的幅值、α1,α2,…,αn分别为构件所受n个不确定外载的方向角；

是当前设计向量ρ所对应结构的体积；v0＝nxny是设计域的体积；是所设计结构占用设计域的体积分数，为常数；

k(x)u＝f(i)是构件平衡方程，其中k(x)是(2nxny)×(2nxny)维总体刚度矩阵，使用经典有限元理论构造，其具体数值受有界概率不确定向量x影响；f(i)是(2nxny)×1维节点力矩阵，使用经典有限元理论构造，其具体数值受区间不确定向量i影响；u是(2nxny)×1维节点位移矩阵；

是颗粒增强材料构件在区间不确定向量i作用下、最差工况的屈服值，其计算方式如下：

a)根据经典有限元方法可以将同时考虑区间与有界概率不确定性作用的结构屈服写作eq.3：

c(ρ,x,i)＝u^tk(x)u＝f(i)^tk^-1(x)f(i)eq.3

b)定义为通过将有界概率不确定向量x中的每一个概率变量取其均值所得的常值向量，称μx为有界概率不确定向量x的均值向量，其中分别为各不确定性x1,x2,…,xm的均值；令结构屈服c(ρ,x,i)中有界概率不确定性向量x＝μx，则此时结构屈服仅包含区间不确定性i的影响，可写作c(ρ,μx,i)＝c(ρ,i)；同时总体刚度矩阵也为常矩阵，可写作k(μx)＝k；

c)将节点力矩阵写成各外载节点力向量之和的形式：

同时有：

式eq.5中，fix＝ficosαi，fiy＝fisinαi分别为外载fi沿x,y轴方向的幅值分量；eix，eiy分别为对应于外载fi所作用节点的、沿x,y轴方向的单位节点力向量；

d)根据线弹性假设，n个不确定载荷的总体作用可以等效为各载荷单独作用效果的叠加：

在eq.6中对不确定载荷的幅值与方向角分别求导可得(i＝1,2,…,n)：

根据eq.7所得导数信息，分别令求解得(i＝1,2,…,n)，即颗粒增强材料构件在区间不确定向量i作用下的最差工况此时最差工况的屈服值可写作

式eq.2中，分别为在有界概率不确定向量x影响下、最差工况的屈服值的均值与标准差，其计算方式如下：

a)还原中的μx为有界概率不确定向量x，此时最差工况的屈服值可写作其中包含概率不确定性；

b)通过rahman多变量函数的单变量降维方法，最差工况的屈服值可通过下式展开：

式eq.8中，m是有界概率不确定性向量x中所包含的有界概率不确定性参数个数，x＜i＞(i＝1,2,…,m)按eq.9定义：

式eq.9中xi是第i个有界概率不确定性变量；

c)根据展开式eq.8，用于计算最差工况屈服值一阶、二阶原点矩的高维积分可以转化为若干一维积分的运算：

式eq.10、eq.11中ψ(xi)是概率不确定性xi(i＝1,2,…,m)的概率密度函数；

d)式eq.10、eq.11中的各一维积分采用拉盖尔(laguerre)积分格式进行计算：

式eq.12中，t是拉盖尔(laguerre)积分点个数，为事先指定的常数；x^(j),λ^(j)(j＝1,2,…,t)分别为标准积分点与其对应权重，通过拉盖尔(laguerre)积分规则给出，均为常数；通过在x＜i＞中令有界概率不确定性变量xi分别为获得，即其中也均为常数，通过对各积分点的等概率变换计算得到，即

e)最差工况屈服值的均值与标准差可通过eq.13获得：

6)采用拓扑优化中的标准最优准则法(standardoptimalitycriteriamethod,ocmethod)迭代求解eq.2的考虑区间与有界概率混合不确定性的颗粒增强材料构件稳健优化设计模型，在每一迭代过程中的计算过程具体为：

6.1)按eq.14定义加权目标函数用于实现的双目标优化：

式eq.14中，j(ρ)为定义的加权目标函数；w为事先指定的权值，为常数；

6.2)按eq.15、eq.16分别计算目标函数与约束函数对各设计变量ρe(e＝1,2,…,nxny)梯度：

6.3)根据所求目标函数与约束函数梯度信息，根据标准最优准则法更新当前设计变量；

6.4)检查本次迭代中目标函数值与上一迭代中目标函数值的差值，对于第一次迭代，该差值被定义为第一代的目标函数值，若该差值小于事先指定的收敛阈值，则称满足收敛条件并输出更新后的设计变量；否则重复步骤6.1)至6.4)。

进一步地，所述步骤1)中，将具有充足样本信息的颗粒增强相在基体中分布的体积分数视为有界概率不确定性处理，具体如下：

颗粒增强相在基体中的体积分数仅沿构件厚度方向(即y轴方向)发生变化，该变化方式具有理论设计表达式vol(y)，但实际制造过程中由于增强颗粒添加料口控制系统的滞后性等因素，颗粒增强相的体积分数具有不确定性，且可通过确定性理论表达式vol(y)与一项不确定参数的乘积来表示，如eq.17所示：

vol^*(y)＝vol(y)·θeq.17

式eq.17中，vol^*(y)是实际制造中颗粒增强相的体积分数变化方式；θ是反映增强相实际体积分数相对理论设计值波动的不确定参数，称为颗粒增强相的体积分数不确定度，其不确定信息可通过测量添加机构的相关参数(给料口响应时滞、添加机构摩阻等)获得。

进一步地，所述步骤1)中，采用服从广义贝塔分布(gbeta分布)的随机变量来描述各有界概率不确定性参数，具体如下：

1.1)对有界概率不确定性参数xi，通过实验获取该参数的s个样本，进而构造样本集根据该样本集，按eq.18计算参数xi的取值范围、按eq.19计算参数xi的均值与方差：

1.2)采用广义贝塔分布描述分布在[ai,bi]内且均值与方差分别为的参数xi，首先标准化其均值与方差如eq.20所示：

然后，采用eq.21计算参数xi的广义贝塔分布的分布参数αi,βi：

记参数xi服从在[ai,bi]内且分布参数为αi,βi的广义贝塔分布，即xi～gbeta(ai,bi|αi,βi)，且其概率密度函数如eq.22所示：

式eq.22中，是参数xi的概率密度函数；γ(·)是伽马函数。

进一步地，所述步骤3.3)中，使用halpin-tsai微观结构模型，计算第i(i＝1,2,…,ny)层内各单元杨氏模量与泊松比具体如下：

3.3.1)增强颗粒的物理属性为：颗粒平均长度lg、平均宽度wg与平均厚度tg、杨氏模量eg等；

3.3.2)定义以下参数：

式eq.23中，em是基体材料的杨氏模量；

3.3.3)第i(i＝1,2,…,ny)层内各单元杨氏模量通过eq.24计算：

式eq.24中，vol^*(i)是第i(i＝1,2,…,ny)层内颗粒增强相的实际平均体积分数，具有概率不确定性；

3.3.4)第i(i＝1,2,…,ny)层内各单元泊松比通过eq.25计算：

式eq.25中，νg、νm分别为第i(i＝1,2,…,ny)层内各单元、增强颗粒、基体材料的泊松比。

进一步地，所述步骤6.2)具体如下：

6.2.1)将eq.10、eq.11代入eq.15：

式eq.26中的梯度项分别为eq.10、eq.11所计算的、最差工况屈服值一阶及二阶原点矩对各设计变量ρe(e＝1,2,…,nx·ny)的梯度；

6.2.2)梯度项具体计算式如eq.27、eq.28所示；

式eq.27、式eq.28中的各梯度项通过经典拓扑优化框架simp给出：

式eq.29中是的简写，其理由在于前述4项中的有界概率不确定性向量均为常值；p是事先指定的常数罚因子；ke是单元e的单元刚度矩阵，可通过经典有限元理论计算；ue是单元e的单元位移矩阵，可通过经典有限元理论从各次有限元方程求解得到的节点位移矩阵u中提取；

6.2.3)将eq.29计算结果代入eq.27、eq.28，并进一步将eq.26、eq.27计算结果代入表达式eq.26中，获得最终目标函数梯度结果。

进一步地，所述步骤6.3)具体如下：

6.3.1)为使用二分查找(bisectionalgorithm)迭代确定适当的约束函数拉格朗日乘子λ用于更新设计变量，首先指定拉格朗日乘子λ的取值上下界λ1、λ2分别为1e-3、1e9；

6.3.2)取当前拉格朗日乘子为取值上下界的平均值如eq.30所示：

λ＝λmiddle＝(λ1+λ2)/2eq.30

6.3.3)按eq.31更新设计变量(e＝1,2,…,nxny)：

式eq.31中，m＝0.2是搜索移动步长；η＝0.5是搜索阻尼系数；be通过目标函数与约束函数梯度信息得到，如eq.32所示：

6.3.4)计算更新后设计变量所对应结构的体积并根据约束函数违反情况调节拉格朗日乘子的取值边界：若收缩取值下界至λ1＝λmiddle；若收缩取值上界至λ2＝λmiddle；

6.3.5)检查二分查找的收敛条件(λ2-λ1)/(λ2+λ1)＜1e-3，若不满足，则返回重复6.3.2)至6.3.5)进行下一次对拉格朗日算子的搜索；若满足，则表明当前拉格朗日算子已满足要求，输出当前设计变量

本发明具有的有益效果是：

1)考虑颗粒增强材料构件在制造与使用过程中的多源不确定性，包括构件基体材料的材料属性、颗粒增强相在基体中分布的体积分数、构件所受外载的幅值与方向；其中，由于难以获得关于外载的充足样本信息，故将其幅值与方向不确定性视为区间不确定性处理；将具有充足样本信息的基体材料材料属性、颗粒增强相材料属性、颗粒增强相在基体中分布的体积分数视为有界概率不确定性处理，并采用广义贝塔分布(gbeta分布)来描述各有界概率不确定性参数，克服了现有产品结构稳健拓扑优化设计方法仅考虑概率不确定性或区间不确定性的不足，所构建的构件稳健优化模型更符合工程实际。

2)借助经典有限元框架，目标性能可以通过设计变量、确定性参数与不确定性参数来显示表达；现有考虑概率区间混合不确定性的构件稳健拓扑优化方法往往首先考虑设计模型中的概率不确定性，接着在目标性能统计矩中引入区间不确定性以估计该统计矩的取值边界，用以表征构件的稳健性能，因此往往不能给出具体的最差工况；现有考虑结构最差工况的构件稳健拓扑优化研究则仅考虑单一类型的不确定性，在不确定性建模方面精度与合理性的不足可能导致优化结果不可靠；本发明在同时考虑混合不确定性前提下，引入线弹性形变假设，即构件在多个区间不确定性外载作用下、最终发生的形变可通过叠加各外载单独作用产生的形变而获得；据此计算目标性能对不确定性外载的梯度信息以获得构件最差目标性能所对应的最差工况，且该求解过程无需重复通过有限元方法求解结构响应，解决了现有混合不确定性稳健拓扑优化方法无法给出最差工况的弊端、为工程师的进一步分析参考提供了理论依据。

3)现有考虑混合不确定性的构件稳健拓扑优化大多基于超材料晶格结构，受限于增材制造的制造精度，实际产品性能相对理论设计结果往往存在差异；因此从实际工业制造可行性与制造水平出发，针对工业制造中已广泛使用的颗粒增强材料，本发明通过考虑颗粒增强相在基体材料中体积分布的不确定性，建立了一种使用颗粒增强材料的构件稳健拓扑优化方法，将现有的针对单一材料的构件稳健优化设计方法推广到复合材料中；同时，该单一宏观层次的构件稳健拓扑优化给出的设计结果在实际制造过程中对增材制造的制造精度能够通过当前水平满足，避免了现有基于晶格结构的多层次稳健优化设计结果在实际制造后的性能劣化，具有较高的工业可行性。

4)现有构件稳健拓扑优化方法由于考虑正态分布的概率不确定性，因此一般采用积分限为正负无穷的厄密特(hermit)积分格式计算目标性能统计矩；但正态分布取值的无界性与实际工程中不确定性参数一般非负的合理取值有冲突，可能造成设计结果不合理；本发明通过引入对所优化目标性能的单变量降维方法与积分限为零至正无穷的拉盖尔积分格式，提出了一种精确估计构件目标性能均值与标准差的数值方法；相较现有考虑概率区间混合不确定性的产品结构性能统计矩估计方法，该方法以更符合实际的有界概率不确定性模型——广义贝塔分布(gbeta分布)为基础、与成熟的稳健拓扑优化框架中具有更好兼容性，且能高效导出目标性能对设计变量的梯度信息用于迭代更新、寻优。

附图说明

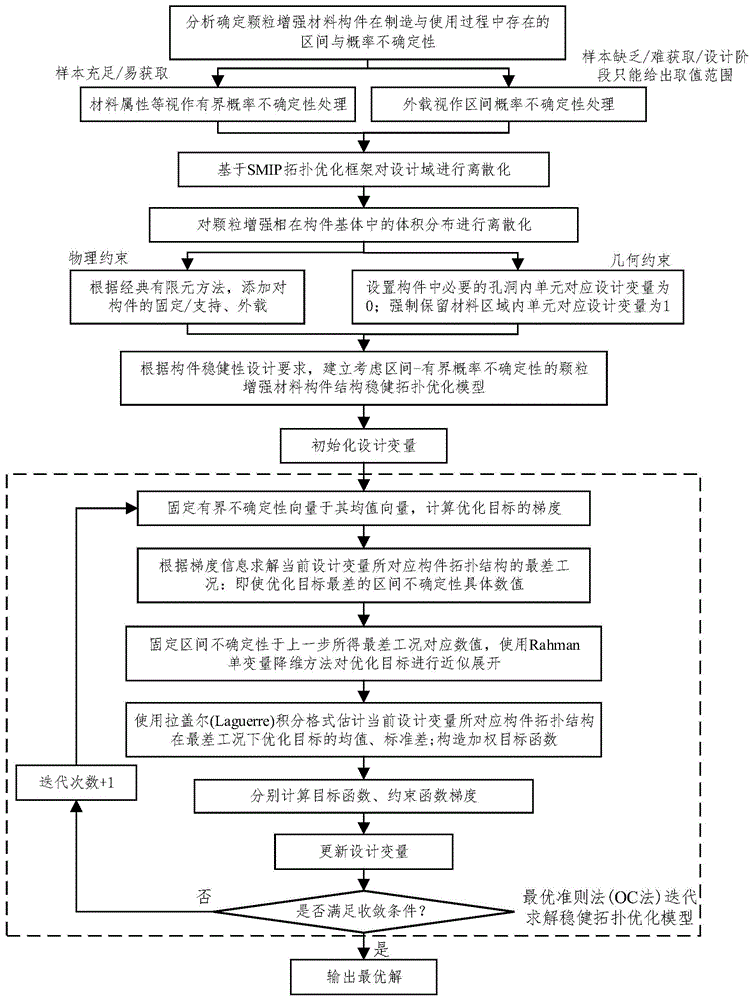
图1是考虑混合不确定性的颗粒增强材料构件稳健拓扑优化方法流程图。

图2是某型号高速压力机结构图(拆除上横梁)。

图3是外连杆初始设计图。

图4是外连杆稳健拓扑优化设计元素示意图。

图5是外连杆稳健拓扑优化设计结果。

图6是根据稳健拓扑优化设计结果得到的外连杆结构设计图。

具体实施方式

以下结合附图和实例对本发明作进一步说明。

图中涉及信息为本发明在某型号高速压力机用外连杆稳健设计中的实际应用数据，图1是考虑混合不确定性的颗粒增强材料构件稳健拓扑优化设计方法流程图。

1、以图2所示使用20％sic颗粒增强al365材料制造的某型号高速压力机用外连杆作为研究对象，考虑该外连杆在制造与使用过程中的不确定性：

1.1)外连杆所受外载由于压力机主轴转速的波动、滑块密度与所冲压材料的不均匀性等而具有一定不确定性，但由于在压力机工作过程中对该外载进行测量有一定困难，难以获得关于外载的充足样本信息，故将其幅值f与方向角视为区间不确定性处理；

1.2)外连杆基体材料al365的材料属性(杨氏模量eal与泊松比νal)由于原材料物性不均一、冶金过程中工艺波动等具有较显著的不确定性，但通过测量成品可获得充足样本信息，故可作为有界概率不确定性处理；sic增强颗粒一般通过溶胶-凝胶法等精密化学方法制得，杨氏模量与泊松比稳定，故不考虑其不确定性而使用其标称值；sic颗粒增强相在al基体中沿厚度方向(即y方向)分布的体积分数vol(y)不确定度θ可通过测量添加机构的相关参数获得充足样本信息，故也作为有界概率不确定性处理；进一步地，以上有界概率不确定性均采用服从广义贝塔分布(gbeta分布)的随机变量来描述，各不确定性变量的参数信息总结如表1所示：

表1外连杆不确定性参数信息汇总表

*对区间变量而言，其不确定性参数为区间中点与半径；对有界概率变量而言，其不确定性参数为其均值与标准差；

2、对该外连杆设计域进行离散化，具体为；

高速压力机外连杆在实际工作过程中一般沿铰接孔轴向方向的外载分力很小，因此简化其受力情况为二维平面应力状态，同时去除倒角、圆角等零件细节以提高计算效率；将化简的外连杆置于一规则矩形设计域内(图4中虚线框围出的范围，其尺寸为x×y＝355mm×180mm)，并将该矩形设计域划分为nx×ny个正方形单元，其中nx，ny分别为沿x,y轴方向的划分数，在本设计中取nx＝710、ny＝360，则每一单元为边长0.5mm×0.5mm的正方形；基于拓扑优化中经典的带罚各向同性材料(smip)框架，每一单元赋予唯一设计变量ρe∈[0,1](e＝1,2,…,710×360)；

3、对sic颗粒增强相在外连杆al365基体中的体积分布进行离散化，具体为：

3.1)根据离散设计域指定坐标系，以外连杆传力方向为x轴，设定坐标系如图4所示，则已离散的各单元节点都可确定坐标；颗粒增强材料外连杆中，颗粒增强相在基体中的体积分数为分层渐变，即颗粒增强相在基体中的体积分数仅沿垂直于连杆传力方向、即图中y轴方向发生变化；由于高速压力机实际工作时要求增强外连杆韧性与耐磨性、减小变形并避免失稳，因此颗粒增强相体积分数的理论表达式vol(y)根据实际使用要求进行选择为：

vol(y)＝20％·cos(πy/y)eq.33

式中y＝180mm为矩形设计域y轴方向长度；sic颗粒增强在外连杆中心的理论体积分数最大、向两边逐渐减小至0，而相同一厚度上颗粒增强相的体积分数为常数；该理论体积分数变化方式是y坐标的连续函数，需要进一步对其离散化；

3.2)根据步骤2中已离散的710×360单元设计域、理论颗粒增强相体积分数变化方式vol(y)，计算第i(i＝1,2,…,360)层内、颗粒增强相的实际平均体积分数vol^*(i)如下：

式eq.34中，θ是颗粒增强相体积分数的不确定度；第i(i＝1,2,…,360)层内全部单元的颗粒增强相体积分数均为以上计算所得vol^*(i)(i＝1,2,…,360)，是层号i的函数；至此颗粒增强相体积分数已被离散；

3.3)使用halpin-tsai微观结构模型，计算第i(i＝1,2,…,360)层内各单元包括杨氏模量在内的各物理参数，具体为：

3.3.1)所添加sic增强颗粒的物理属性为：颗粒平均长度lg＝1μm、平均宽度wg＝0.4μm与平均厚度tg＝0.4μm、杨氏模量eg＝400gpa、泊松比νg＝0.17；

3.3.2)定义以下参数：

3.3.3)第i(i＝1,2,…,360)层内各单元杨氏模量计算如下(单位gpa)：

3.3.4)第i(i＝1,2,…,360)层内各单元泊松比计算如下：

3.4)基于拓扑优化中经典的带罚各向同性材料(smip)框架，引入罚因子p＝3，并指定最小杨氏模量允许值emin＝1e-3gpa，则第i(i＝1,2,…,360)层内各单元的杨氏模量最终可表达为：

4、依据经典有限元方式，对已离散化的结构施加物理约束与几何约束，具体为：

4.1)几何约束：图3外连杆原始设计中φ60与φ110铰接孔保留，设置两处孔内(图4中区域i)无材料，即孔内全部单元所对应设计变量ρe≡0；图3外连杆原始设计中两连接套筒(左套筒内径φ60外径φ90，右套筒内径φ110外径φ180)环形结构保留材料，设置这两处圆环区域内(图4中区域ii)全部单元所对应设计变量ρe≡1；两个铰接孔之间的连接板拓扑结构是需要优化设计的对象，因此对该外连杆进行的稳健拓扑优化实际是针对图4中设计域内除去i与ii的区域、即两个铰接孔之间的连接板进行的；设置完成后如图4所示；

4.2)物理约束：依据经典有限元方法框架，设置图3中φ60铰接孔内壁对应的单元为固定约束，图3中φ110铰接孔中心施加水平向左的径向力，该径向力具有不确定性幅值f与不确定性方向角设置完成后如图4所示；

5、将外连杆结构屈服作为优化目标、将最差工况下结构屈服的均值与标准差作为优化目标，建立考虑区间与有界概率混合不确定性的颗粒增强材料外连杆稳健拓扑优化设计模型如下所示：

式中，ρ＝(ρ1,ρ2,…,ρ710×360)^t是(710×360)×1维设计向量，ρmin＝0.001是设计中给定的各设计变量最小允许值；x＝(ρal,νal,θ)^t是3×1维有界概率不确定性向量；是2×1维区间不确定性向量；

是当前设计向量ρ所对应结构的体积；v0＝710×360是设计域体积；是设计中给定的结构体积最大允许值；

k(x)u＝f(i)是外连杆平衡方程，其中k(x)是2(710×360)×2(710×360)维整体刚度矩阵；f(i)是2(710×360)×1维节点力矩阵；u是2(710×360)×1维节点位移矩阵；是sic颗粒增强al材料外连杆在区间不确定向量i作用下、最差工况的屈服值；分别为在有界概率不确定向量x影响下、最差工况的屈服值的均值与标准差；

sic颗粒增强al材料外连杆在区间不确定向量i作用下的最差工况通过以下步骤确定：

a)根据经典有限元方法，同时考虑区间与有界概率不确定性作用的结构屈服可以写作：

c(ρ,x,i)＝u^tk(x)u＝f(i)^tk(x)^-1f(i)eq.40

b)定义为通过将有界概率不确定向量x中的每一个概率变量取其均值所得的常值向量，称μx为有界概率不确定向量x的均值向量，其中μθ分别为不确定性ρal,νal,θ的均值；令结构屈服c(ρ,x,i)中有界概率不确定性向量x＝μx，则此时结构屈服仅包含区间不确定性i的影响，可写作c(ρ,μx,i)＝c(ρ,i)；同时总体刚度矩阵也为常矩阵，可写作k(μx)＝k；

c)将节点力矩阵写成各外载节点力向量之和的形式，该连杆只包含一个不确定性外载，因此有：

同时有：

式中，分别为外载f沿x,y轴方向的幅值分量；ex，ey分别为对应于外载f所作用节点的、沿x,y轴方向的单位节点力向量；

d)根据线弹性假设，有：

在上式中对不确定载荷的幅值与方向角分别求导可得：

根据该所得导数信息，分别令求解得颗粒增强材料外连杆在区间不确定向量i作用下的最差工况则最差工况的屈服值

在有界概率不确定向量x影响下、最差工况的屈服值的均值与标准差通过以下步骤确定：

a)还原中的μx为有界概率不确定向量x，此时最差工况的屈服值可写作其中包含概率不确定性；

b)通过多变量函数的单变量降维方法，最差工况的屈服值可通过下式展开：

式中，x＜i＞(i＝1,2,3)分别如下：

c)根据b)中展开式，用于计算最差工况屈服值一阶、二阶原点矩的高维积分可以转化为若干一维积分的运算：

式eq.47、eq.48中ψ(xi)是概率不确定性xi(i＝1,2,3)的概率密度函数；

采用拉盖尔(laguerre)积分格式计算以上式中的各一维积分：

式中，t是拉盖尔(laguerre)积分点个数，在此指定t＝6；x^(j),λ^(j)(j＝1,2,…,6)分别为标准积分点与其对应权重，通过拉盖尔(laguerre)积分规则给出；

d)最差工况屈服值的均值与标准差可通过下式获得：

6、采用最优准则法(optimalitycriteriamethod,ocmethod)迭代求解考虑区间与有界概率混合不确定性的sic颗粒增强al材料外连杆稳健优化设计模型：

6.1)初始化设计变量为

下面以第1次迭代过程为例说明基于最优准则法的颗粒增强连杆直接解法流程：

6.2)按下式定义加权目标函数j(ρ)用于实现的双目标优化：

6.3)目标函数与约束函数对各设计变量ρe(e＝1,2,…,710×360)梯度可通过下式分别计算：

6.3.1)为获得目标函数梯度，需要将eq.50代入eq.52，得到：

6.3.2)eq.52中梯度项(e＝1,2,…,710×360)具体计算式如下所示；

式eq.55、eq.56中的各梯度项(e＝1,2,…,710×360)通过经典拓扑优化框架simp给出：

式eq.57中，是的简写，其理由在于前述4项中的有界概率不确定性向量均为常值；ke是单元e的单元刚度矩阵，可通过经典有限元理论计算；ue是单元e的单元位移矩阵，可通过经典有限元理论从各次有限元方程求解得到的节点位移矩阵u中提取；

6.3.3)将全部计算结果代入目标函数梯度表达式eq.3-22中，获得最终目标函数梯度结果，截取如下：

且有目标函数值j(ρ)＝2054.920mm；

6.4)根据上述所求目标函数与已得约束函数梯度信息更新设计变量，截取部分如下：

ρ1＝0.294,ρ1＝0.320,…,ρ710×360-1＝0.215,ρ710×360＝0.186eq.59

6.5)检查本次迭代中目标函数值与上一迭代中目标函数值的差值，由于用于演示的是第一次迭代，该差值被定义为当前目标函数值158.2399，不满足收敛阈值0.01，因此重复步骤6.1)至6.5)。

最终获得的最优解截取部分如下：

ρ1＝0,…,ρ16247＝4.28e-31,…,ρ16252＝1,…,ρ710×360＝0eq.60

迭代寻优在第379代收敛，最优解对应的结构、与结构中增强相的体积分数云图如图5所示；最优解的结构性能为对应该最优解的最差工况为该值可用于进一步工程分析；满足面向颗粒增强材料的高速压力机外连杆稳健性设计需求与工作要求，从而验证了所提出方法的有效性；对该稳健拓扑优化结果进行轮廓平滑、并根据实际需要设置倒角、圆角等零件结构后，最终获得的外连杆设计图如图6所示。

需要声明的是，本发明内容及具体实施方式意在证明本发明所提供技术方案的实际应用，不应解释为对本发明保护范围的限定。在本发明的精神和权利要求的保护范围内，对本发明作出的任何修改和改变，都落入本发明的保护范围。