一种基于基于自适应大邻域搜索算法的城轨列车时刻表节能优化方法

本发明涉及到地铁列车节能技术领域，为了提高再生制动能量的利用率，本文提出了一种基于自适应大邻域搜索算法的种基于自适应大邻域搜索算法的城市轨道交通列车运行调整策略，使制动列车所产生的再生制动能量可以直接用于正在加速的列车。此外，设计了一种自适应大邻域搜索算法(alns)来求解模型得到最优时间表。

背景技术：

城市轨道交通，作为城市公共交通系统的一个重要组成部分，以其运量大、快速准时、安全高效、节能环保等优点很好地解决了城市交通增长的供需矛盾和道路拥堵问题。但在列车运营过程中会产生大量的能源消耗，如何降低列车运营能耗成为了当下研究热点。传统的轨道交通节能研究主要通过减少列车质量，降低列车运行阻力从而改变列车速度曲线来降低列车运行牵引能耗，此类方法研究已经比较成熟。近年来，如何通过优化列车运行时刻表来提高列车再生制动能量的利用率得到越来越多的关注和研究。所谓的再生制动能量就是将列车运行的动能转化成能够通过转换器和受电弓反馈到供电触网的电能。

当今，随着再生制动技术在城市轨道系统的广泛应用，急需一种既能满足节能又能较好地运用于实际运营的多列车节能时刻表。这种时刻表一般有以下几个特点：(1)节能效果好：通过建立多列车节能运行优化模型，改变列车的发车时间间隔和在每站的驻留时间尽可能提高再生制动能量的利用率；(2)保证完成运输任务：不改变列车在每个区间的运行时间，即保证列车的原定运行速度曲线，只对列车的发车时间间隔，驻留时间做一定范围的调整，保证经过优化后的列车在节能的同时能完成运输任务；(3)容易实现：只对列车时刻表进行离线优化，优化后的时刻表作为参考供列车使用，而不是直接对列车进行实时控制，同时模型应该尽量简单，决策变量应该尽量少以简化求解难度。

技术实现要素：

为了满足上述时刻表的特点，本发明提供了一种基于自适应大邻域搜索算法的列车时刻表节能优化方法，首先，提出了协同调度的规则，定义了高峰时段和非高峰时段的加速列车和制动列车之间的重叠时间。其次，建立了列车时刻表整数规划模型，使重叠时间最大化。除此之外，为了保证列车运输任务以及简化模型，本发明将最终的决策变量简化为两个，大大降低了模型求解难度。最后本发明设计出一种自适应大邻域搜索算法来快速求解此类问题，目前国内鲜有使用该算法来解决此类问题的例子，且本文还设计了专门适用于模型的算子，大大减少了运算时间。在构建模型时需要对模型进行一些列假设：(1)制动列车产生的再生制动能量可以反馈到高架接触线，并立即被加速列车使用，能量的转化和传输损耗为一个定值。(2)城市轨道交通站间距较短，不存在3辆车同时处于同一供电分区的情况。(3)列车上行和下行的架空接触线设备是相互独立的，即上行列车的再生制动能量不能传输到下行列车。(4)除发车时间间隔外，所有开往同一方向的列车都有一个共同的时刻表，这意味着它们在每个车站停留的时间和在每个路段行驶的时间都是相同的，并且所有列车的制动时间都相同，为一个定值。

建立模型所用的一些参数及变量见表1

表1建立模型所用变量

本发明采用了如下的技术方案及实现步骤：

a.模型构建阶段：

步骤1：时刻表模型构建：构建时刻表模型的目的为计算相邻两辆列车的牵引制动重叠时间，使重叠时间在约束条件内达到最大。列车运行高峰期以及非高峰期，列车的发车间隔，停站时间会有显著不同，故在建立模型时分别建立在列车运行高峰期以及非高峰期的模型。

(1.1)列车运行高峰期：列车运行高峰期，由于列车发车间隔小，相邻列车间隔较近，通常运行在同一个区间。在阶段1,列车i正在牵引加速离开第n站前往第n+1站，同一时刻，列车i+1正在制动减速停往n站。阶段2，列车i正在制动减速准备停往n+1站；同一时刻，列车i+1正在牵引加速离开n站。定义f1(t,b)为列车运行高峰期阶段1的牵引制动重叠时间计算函数，计算公式为：

其中n代表第n个车站，i代表第i辆列车，表示第i辆列车在第n站的出站时刻；代表第i辆列车到达第n站的时刻；代表第i辆列车在区间(n,n+1)牵引工况结束时刻；代表第i辆列车在区间(n,n+1)制动工况开始时刻；

定义f2(t,b)为列车运行高峰期阶段2的牵引制动重叠时间计算函数，计算公式为：

经总结，列车运行高峰期的牵引制动重叠时间的可以用fp表示：

其中当第n代表车站数，i代表列车数；当第n-1站与第n站位于同一个供电区间时λ(n-1,n)＝1，否则λ(n-1,n)＝0；

(1.2)列车运行非高峰期：列车运行非高峰期，发车间隔大，相邻列车间隔较远，通常运行于不同区间。在阶段1，列车i+1正在制动减速停往n站，同一时刻，列车i在牵引加速驶离n+1站；阶段2，列车i正在制动减速准备停往n+2站，同一时刻，列车i+1正在牵引加速驶离n站。定义f3(t,b)为列车运行非高峰期阶段1的牵引制动重叠时间计算函数，计算公式为：

定义f4(t,b)为列车运行非高峰期阶段2的牵引制动重叠时间计算函数，计算公式为：

经总结，列车运行非高峰期的牵引制动重叠时间的可以用fop表示：

步骤2：模型化简：步骤1的得到列车时刻表模型涉及的决策变量有四个分别为决策变量太多导致计算量增大，模型变复杂，故考虑将模型进行简化。定义h为列车的发车间隔，t(n,n+1)为列车运行在区间(n,n+1)运行时长，为列车在区间(n,n+1)处于牵引工况的时长，为列车在区间(n,n+1)处于制动工况的时长，xn为列车在第n站的停站时间，其中i＝1,2,3,…,i，n＝1,2,3,…,n。

可以知道：将以上表达式代入公式(3)和(6)得到：

其中x＝xn＝(x1,x2,x3,...,xn-1)。

步骤3：得出目标函数：

经过上述分析，得到最终的时刻表优化目标：

约束条件有四个，第一个为停站时间约束，其上、下限分别为lh和uh；第二个约束为列车在每站的驻留时间，其上、下限分别为ln和un；第三个约束为正整数约束，z代表正整数集合；第四个约束条件为总行程时间的约束，其上、下限分别为lt和ut，r(n,n+1)代表列车在区间n的运行时间。

b.算法设计阶段：

步骤4：自适应大邻域搜索算法：自适应大邻域搜索算法中的邻域是由destroy和repair方法隐式定义的。destroy方法会破坏当前解的一部分，而后repair方法会对被破坏的解进行重建。那么，解x的邻域n(x)就可以定义为：首先通过利用destroy方法破坏解x，然后利用repair方法重建解x，从而得到的一系列解的集合，但alns算法不会搜索解的整个邻域，而只是对该邻域进行采样搜索，也就是说，如此大的邻域是不可能一一遍历进行搜索的，只能采样搜索其中的一些解而已。具体的算法步骤如下：

step1：设置初始解x,设置destroy方法集合和repair方法集合的权重；

step2：将初始解赋值给目前为止获得的最优解x^b；

step3：根据destroy方法集合和repair方法集合的权重来选择destroy方法和repair方法，权重大的优先被选中；

step4：使用destroy方法和repair方法对解x进行重构得到解x的邻域；

step5：在邻域中搜索由于当前解x的新解；

step6：如果找到新的解，则算法停止，否则重复步骤2-6；

有益效果

本发明建立的列车时刻表优化模型具有良好的优化效率，在列车运行高峰期以及非高峰期均可以提高列车再生制动能量的利用率。

附图说明

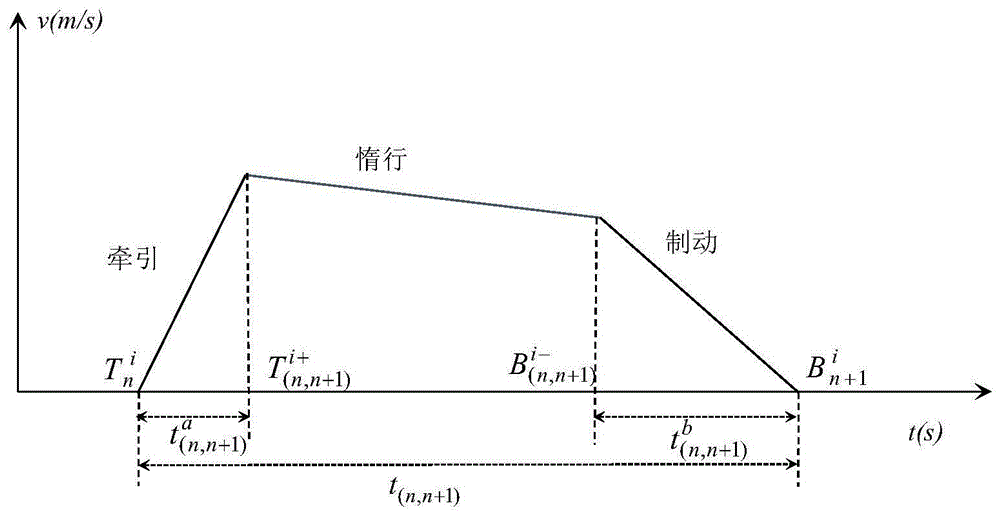
图1为列车在区间n运行的速度曲线图；

图2为列车运行高峰期示意图；

图3为列车运行高峰期重叠时间示意图；

图4为列车运行非高峰期示意图；

图5为列车运行非高峰期重叠时间示意图；

具体实施方式

北京地铁亦庄线14个车站，6个变电所，站间距及变电所覆盖范围见表3。

表2北京地铁亦庄线数据

本实验即以北京地铁亦庄线为研究对象，列车总质量为287080kg,动能转换为再生制动能的转换因子θ1＝0.6，再生制动能的传输损耗因子θ2＝0.1，制动工况减速度an＝0.4m/s²，列车在区间n处于制动工况的时长

将本发明方法应用到上述北京地铁亦庄线对象包括“模型构建”和“算法设计”两个大步骤，具体陈述如下：

a.模型构建阶段：

步骤1：模型假设；

步骤2：参数设置：根据北京地铁亦庄线路的实际运行时刻表及客流数据，列车运行高峰期，平均1小时发车数量为20辆，即i＝20；非列车运行高峰期，平均1小时发车数量为12辆，即i＝12。

步骤3：模型构建；

步骤4：得到目标函数；

步骤5：再生制动能量的计算:列车在制动阶段为匀减速运动，在计算减速阶段所产生的动能时也可以将其看作为加速度为an，初速度为0的匀加速运动，其产生的动能为：

其中vb为列车在制动阶段的瞬时速度且:

vb＝ant

其中t为制动阶段运行时间。结合动能转换为再生制动能的转换因子θ1，以及再生制动能的传输损耗因子θ2，得到列车在制动阶段产生

再生制动能量为:

由公式可知，再生制动能量与t²成正比，故在重叠时间内可利用的再生制动能量的为:

式中，t代表制动总时间，eu代表可利用的再生制动能量。f(x,h)代表牵引制动重叠时间。

b.算法设计阶段：

步骤6：自适应大邻域搜索算法设计：为了提高自适应的大邻域搜索算法的求解效率，设计了3种destroy方法，分别为：(1)randomdestroy(随机移除算子)：随机移除解向量中的一些值；(2)associateddestroy(关联节点移除算子)：定义关联结点，每次选择与上一个移除的值关联度较高的值进行移除；(3)worstcostdestroy(最大影响移除算子)：选择所有值中对目标函数值影响最大的进行移除。还设计了2种repair方法，分别为：(1)randomrepair(随机插入算子)；(2)greedyrepair(贪婪插入算子)：评估每个结点的最优插入位置，进行插入操作。

上述步骤即为本发明方法在北京地铁亦庄线列车时刻表上的具体应用。为了验证方法的有效性，应用实际数据进行了一系列实验。列车运行高峰期，通过计算得到优化后的列车时刻表见表4。发车间隔为90s,重叠时间为3154s,制动总时间t＝9100s，可利用再生制动能量为131.8057kw·h。而当发车间隔为90s时，未优化时刻表的重叠时间为2584s,可利用的再生制动能量为88.4650kw·h。表3为北京地铁亦庄线现行时刻表，表5为列车运行高峰期优化后时刻表。结果表明，优化后的列车时刻表相比于优化前，再生制动能量利用率提高49.50％。

表3北京地铁亦庄线现行时刻表

表4列车运行高峰期优化后时刻表

列车运行非高峰期，通过计算得到优化后的列车时刻表见表。发车间隔为213s,重叠时间为1001s，制动总时间t＝5460s，可利用再生制动能量为22.1274kw·h。而当发车间隔为213s时，未优化时刻表的重叠时间为869s，可利用的再生制动能量为16.6764kw·h。表6为列车运行非高峰期优化后时刻表。结果表明，优化后的列车时刻表相比于优化前，再生制动能量利用率提高32.79％。

表5列车运行非高峰期优化后时刻表

结果表明，与现行列车时刻表相比，本发明建立的列车时刻表优化模型具有良好的优化效率，在列车运行高峰期以及非高峰期均可以提高列车再生制动能量的利用率。