基于EACFZNN模型求解时变李雅普诺夫方程

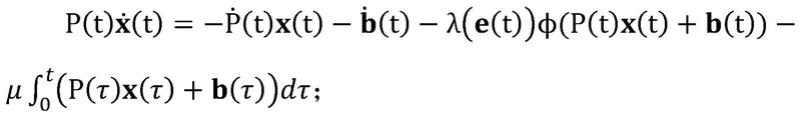
基于eacfznn模型求解时变李雅普诺夫方程
技术领域
1.本发明涉及时变李雅普诺夫方程和神经网络技术领域，具体涉及基于误差的自适应系数负反馈零化神经网络(error based adaptive coefficient negative feedback zeroing neural network，简称eacfznn)求解时变李雅普诺夫方程的方法。


背景技术：

2.李雅普诺夫方程的求解在稳定性分析、多智能体网络系统、拓扑重构、优化问题等许多研究领域都是必不可少的。由于处理矩阵计算对高性能算法的强烈需求，出现了许多优秀的算法(如并行型算法)，它们可以分为两类:数值算法和递归神经网络(rnn)算法。在数值算法方面，基于梯度的迭代算法和newton-raphson迭代(nri)算法是两种比较流行的方法。研究表明有一种参数可调的基于梯度的迭代算法，与现有同类算法相比，收敛速度更快，结构更简单。此外，研究人员还提出了一种基于准梯度的算法，在求解非线性矩阵方程时可以避免矩阵逆运算。对于递归神经网络(rnn)而言，研究人员设计了一种基于梯度的rnn模型用于求解时不变李雅普诺夫方程，当时间趋于无穷时，解的误差可以减小到零。而对于时变情况，由于不考虑时变系数的速度补偿，解的误差总是振荡的。因此，提出了求解各种时变问题的张神经网络(znn)，该网络在收敛性上有显著的改进，与基于梯度的rnn相比，znn能有效地避免解误差的振荡，并能以指数形式收敛于时变李雅普诺夫方程的理论解。之后，研究人员提出了一种新的非线性函数(符号双幂函数)来激活时变时变李雅普诺夫方程的znn，使其收敛性能够达到有限时间收敛。然而，由于深入研究，符号双功率激活函数对于有限时间收敛有一个相对多余的公式。另外，还有很多改进的znn模型被设计，值得进一步注意的是，正如我们上面提到的，在现阶段，大多数的znn模型都可以用来求解时变李雅普诺夫方程，重要的是怎样提高模型的收敛精度和增加抗噪性。


技术实现要素：

3.(一)解决的技术问题
4.本发明目的在于解决背景技术提出的问题，而提出了基于eacfznn模型求解时变李雅普诺夫方程。
5.(二)技术方案
6.基于eacfznn模型求解时变李雅普诺夫方程：包括：
7.a.首先建立求解时变李雅普诺夫方程的数学模型
；
8.b.定义基于误差的自适应系数负反馈神经网络，讨论其收敛性；
9.c将噪声加入模型，讨论在噪声影响下模型的稳定性(即鲁棒性)；
10.d.设定参数，进行结果验证和分析。
11.优选的，步骤a中，建立求解时变李雅普诺夫方程的数学模型，包括以下步骤：
12.a1.李雅普诺夫方程表示为：
13.a
t
(t)x(t)+x(t)a(t)+c(t)＝0；
14.a2.方程两边同时向量化，可得到：
15.vec(a
t
(t)x(t)+x(t)a(t))＝-vec(c(t))；
16.a3.由克罗内克积性质可得：
[0017][0018]
其中，符号表示克罗内克积；令x(t)＝vec(x(t))，b(t)＝vec(c(t))，则有如下式子：
[0019]
p(t)x(t)+b(t)＝0；
[0020]
那么误差函数被写为：
[0021]
e(t)＝p(t)x(t)+b(t)；
[0022]
a4.由oznn模型可得：
[0023][0024]
a5.由tznn模型可得：
[0025][0026]
其中，表示为激励函数，表述为：
[0027][0028][0029][0030]
优选的，步骤b中，定义基于误差的自适应系数负反馈神经网络及其收敛性的判定，包括如下：
[0031]
b1.基于误差范数的自适应系数为：
[0032][0033]
其中，r＞1，是一个常数；
[0034]
b2.定义一个基于误差的自适应系数负反馈神经网络如下：
[0035][0036]
其中μ＞0，是一个常数；
[0037]
b3.求解时变李雅普诺夫方程的基于误差的自适应系数负反馈神经网
[0038]
络，表述为：
[0039][0040]
b4.该神经网络的子系统表达如下：
[0041][0042]
其中，i∈1，2，3....n；
[0043]
b5.定义一个李雅普诺夫候选函数为：
[0044][0045]
其中k＞0，
[0046]
步骤b5中，gi(t)是正定的；
[0047]gi
(t)的时间导数可以描述为：
[0048][0049]
由李雅普诺夫稳定理论可知系统是稳定的，由此证明了模型的收敛性。
[0050]
优选的，步骤c中，引入噪声的模型及其稳定性(即鲁棒性)的判定，
[0051]
具体步骤为：
[0052]
c1.引入噪声后，其基本模型为：
[0053][0054]
c2.并根据噪声类型，进行对应的稳定性判定。
[0055]
其中，
[0056]
若ξi(t)为常数噪声，ξi(t)＝ξ，根据拉普拉斯变换，得到：
[0057][0058]
整理得：
[0059][0060]
这里有当时间无限时，系统的两个极点分别为：
[0061][0062]
因为σ＞0，μ＞0，两个极点在左半平面，有以下等式：
[0063]
[0064]
由此证明了模型在常数噪声的影响下仍然可以保持稳定性；
[0065]
其中，
[0066]
若ξi(t)为线性噪声ξi(t)＝ξit，相似地有模型的拉普拉斯变换如下：
[0067][0068]
根据拉普拉斯终值定理，则：
[0069][0070]
当μ
→
∞，
[0071]
由此表明模型在线性噪声的影响下仍然可以保持稳定性；
[0072]
其中，
[0073]
若ξi(t)为随机噪声ξi(t)＝ζi(t)，相似地有基本模型如下：
[0074][0075]
令那么上面那个式子可写为：
[0076][0077]
除此之外，定义分以下几种情况：
[0078]
c21.σ2＞4μ；
[0079][0080]
之后有如下不等式成立：
[0081][0082][0083]
这里的sup(
·
)代表函数的上界；
[0084]
c22.σ2＝4μ；
[0085]
[0086]
假设ρ＞0，γ＞0，以下等式成立：
[0087]
|ε1texp(ε1t)|＜ρexp(-γt)；
[0088]
因此有如下不等式：
[0089][0090]
则有结论
[0091]
c23.σ2＜4μ；
[0092]
与上面两种情况相似，有如下结论：
[0093][0094]
综上所述，模型在随机噪声的影响下依然可以保持稳定性。
[0095]
优选的，步骤d中，结果验证与分析具体步骤为：
[0096]
d1.给定实例为：
[0097][0098][0099]
d2.微调r和μ的取值，代入模型，使实验结果符合预期，以证明模型的有效性。
[0100]
(三)有益效果
[0101]
本发明公开了基于eacfznn模型求解时变李雅普诺夫方程，改进之处在于：
[0102]
1)定义了一个基于误差的自适应系数，将神经网络求解目标函数的残差再反馈回神经网络，在实际应用中可以更稳定和灵活多变。
[0103]
2)由基于误差的自适应系数负反馈神经网络修正了有些znn模型在噪声干扰下无法稳定的缺陷，即修正的znn模型在噪声干扰的情况仍然可以精确地求解时变李雅普诺夫方程。
[0104]
3)该并行计算模型将问题转化为线性方程的寻零问题，用于求解时变李雅普诺夫方程。
附图说明
[0105]
图1为本发明eacfznn方法流程图。
[0106]
图2为本发明实施例使用eacfznn模型的计算解和理论解轨迹之间的比较图，
[0107]
图3为本发明实施例在r＝3和μ＝10时在不同噪声影响下的eacfznn模型模拟结果。
具体实施方式
[0108]
为了使本领域的普通技术人员能更好的理解本发明的技术方案，下面结合附图和实施例对本发明的技术方案做进一步的描述。
[0109]
参照附图1，基于eacfznn模型求解时变李雅普诺夫方程，包括：
[0110]
a.首先建立求解时变李雅普诺夫方程的数学模型；
[0111]
a1.李雅普诺夫方程表示为：
[0112]at
(t)x(t)+x(t)a(t)+c(t)＝0；
[0113]
a2.方程两边同时向量化，可得到：
[0114]
vec(a
t
(t)x(t)+x(t)a(t))＝-vec(c(t))；
[0115]
a3.由克罗内克积性质可得：
[0116][0117]
其中，符号表示克罗内克积；令x(t)＝vec(x(t))，b(t)＝vec(c(t))，则有如下式子：
[0118]
p(t)x(t)+b(t)＝0；
[0119]
那么误差函数被写为：
[0120]
e(t)＝p(t)x(t)+b(t)；
[0121]
a4.由oznn模型可得：
[0122][0123]
a5.由tznn模型可得：
[0124][0125]
其中，表示为激励函数，表述为：
[0126][0127][0128][0129]
b.定义基于误差范数的自适应零化神经网络，讨论其收敛性；
[0130]
b1.基于误差范数的自适应系数为：
[0131][0132]
其中，r＞1，是一个常数；
[0133]
b2.定义一个基于误差的自适应系数负反馈神经网络如下：
[0134][0135]
其中μ＞0，是一个常数；
[0136]
b3.求解时变李雅普诺夫方程的基于误差的自适应系数负反馈神经网
[0137]
络，表述为：
[0138][0139]
b4.该神经网络的子系统表达如下：
[0140][0141]
其中，i∈1，2，3....n；
[0142]
b5.定义一个李雅普诺夫候选函数为：
[0143][0144]
其中k＞0，
[0145]
步骤b5中，gi(t)是正定的；
[0146]gi
(t)的时间导数可以描述为：
[0147][0148]
由李雅普诺夫稳定理论可知系统是稳定的，由此证明了模型的收敛性。
[0149]
c.将噪声加入模型，讨论在噪声影响下模型的稳定性(即鲁棒性)；
[0150]
c1.引入噪声后，其基本模型为：
[0151][0152]
c2.并根据噪声类型，进行对应的稳定性判定。
[0153]
其中，
[0154]
若ξi(t)为常数噪声，ξi(t)＝ξ，根据拉普拉斯变换，得到：
[0155][0156]
整理得：
[0157][0158]
这里有当时间无限时，系统的两个极点分别为：
[0159]
[0160]
因为σ＞0，μ＞0，两个极点在左半平面，有以下等式：
[0161][0162]
由此证明了模型在常数噪声的影响下仍然可以保持稳定性；
[0163]
其中，
[0164]
若ξi(t)为线性噪声ξi(t)＝ξit，相似地有模型的拉普拉斯变换如下：
[0165][0166]
根据拉普拉斯终值定理，则：
[0167][0168]
当μ
→
∞，
[0169]
由此表明模型在线性噪声的影响下仍然可以保持稳定性；
[0170]
其中，
[0171]
若ξi(t)为随机噪声ξi(t)＝ζi(t)，相似地有基本模型如下：
[0172][0173]
令那么上面那个式子可写为：
[0174][0175]
除此之外，定义分以下几种情况：
[0176]
c21.σ2＞4μ；
[0177][0178]
之后有如下不等式成立：
[0179][0180][0181]
这里的sup(
·
)代表函数的上界；
[0182]
c22.σ2＝4μ；
[0183][0184]
假设ρ＞0，γ＞0，以下等式成立：
[0185]
|ε1texp(ε1t)|＜ρexp(-γt)；
[0186]
因此有如下不等式：
[0187][0188]
则有结论
[0189]
c23.σ2＜4μ；
[0190]
与上面两种情况相似，有如下结论：
[0191][0192]
综上所述，模型在随机噪声的影响下依然可以保持稳定性。
[0193]
d.设定参数，进行结果验证和分析。
[0194]
d1.给定实例为：
[0195][0196][0197]
d2.微调r和μ的取值，代入模型，使实验结果符合预期，以证明模型的有效性。
[0198]
具体计算实施例如下：
[0199]
利用本发明基于零化神经网络求解时变李雅普诺夫方程的方法进行计算：
[0200]
实例如下：
[0201][0202][0203]
(1)在这个实例中，r＝3，μ＝10；
[0204]
(2)将实例带入eacfznn模型，进行计算。
[0205]
计算解和理论解轨迹比较和误差图如图2、图3所示，其中图2为实例在eacfznn模型的计算解和理论解轨迹之间的比较图；图3中(a)为实例在无噪声情况下的残差图，图3中(b)为实例在常数噪声情况下的残差图，图3中(c)为实例在线性噪声情况下的残差图，图3中(d)为实例在随机噪声情况下的残差图。
[0206]
从图中可以看出eacfznn模型作用下，计算解可以很快收敛到理论解，误差也可以很快收敛到零，从而证明了eacfznn模型的有效性和优越性。
[0207]
以上显示和描述了本发明的主要特征和本发明的优点。本行业的技术人员应该了解，本发明不受上述实施例的限制，在不脱离本发明精神和范围的前提下，本发明还会有各种变化和改进，这些变化和改进都落入要求保护的本发明范围内。本发明要求保护范围由所附的权利要求书及其等效物界定。