一种考虑水压的泡沫改良土渗透系数计算方法

1.本发明属于盾构渣土改良技术领域，特别是指一种考虑水压的泡沫改良土渗透系数计算方法。


背景技术：

2.土压平衡盾构因其安全、高效而广泛应用于城市隧道建设，不可避免地会穿越富水砂性地层，在此类地层掘进时极易发生喷涌事故，进而影响掌子面的稳定性，甚至造成地表塌陷等灾害。喷涌事故与渣土本身的渗透性密不可分，通常向土仓中注入泡沫以提高土仓与螺旋机中渣土的抗渗性，通常要求泡沫改良土的渗透系数应维持在10-5
m/s以下至少90min。目前关于泡沫改良土渗透系数的识别主要通过室内外试验直接测量，其测量过程复杂，且需要大型渗透仪辅助才能完成。而关于泡沫改良土渗透系数的理论计算方面相对匮乏，尽管有学者提出了一些关于泡沫改良土渗透系数计算方法，但未能考虑水压对渗透系数的影响。


技术实现要素：

3.针对现有技术的不足之处，基于泡沫渗流理论，本发明提出一种考虑水压的泡沫改良土渗透系数计算方法，能够较为准确地预测泡沫改良土的渗透系数。
4.为实现上述技术目的，本发明采用如下技术方案：
5.一种考虑水压的泡沫改良土渗透系数计算方法，包括：：
6.确定泡沫改良土渗流方向两端分别在各自水压下的泡沫有效粒径以及孔隙比；
7.若渗流流入端的泡沫孔隙比小于或等于预设的孔隙比临界值e
fδ
，则采用公式(01)来根据泡沫有效粒径和孔隙比计算泡沫改良土渗流方向两端的渗透系数k1,k2，并直接根据k1,k2计算泡沫改良土的等效渗透系数k；
8.若渗流流入端的泡沫孔隙比大于预设的孔隙比临界值e
fδ
，且渗流流出端的泡沫孔隙比小于预设的孔隙比临界值e
fδ
，则：采用公式(01)计算泡沫改良土渗流流出端的渗透系数k1和泡沫改良土在孔隙比临界值e
fδ
对应位置δ处的渗透系数k
δ
，采用公式(02)计算泡沫改良土渗流流入端的渗透系数k2，然后根据k1,k2和k
δ
计算等效渗透系数k；
[0009][0010][0011]
式中：x用于区分泡沫改良土渗流方向的不同位置，x＝2和x＝1分别对应流入端和流出端，x＝δ表示孔隙比临界值e
fδ
对应的位置；k
x
为泡沫改良土渗流方向在位置x处的渗透系数；e
fx
为泡沫改良土在位置x处水压p
x
下的泡沫孔隙比，d
10,fx
表示泡沫改良土在位置x处水压p
x
下的泡沫有效粒径；
[0012]ck
为kozeny常数，为无量纲比表面积，u为无量纲过剩能量密度，为泡沫相对于土颗粒的细度，d
10,f
表示泡沫在大气压p下的有效粒径，d
10,s
为土颗粒的有效粒径，n为泡沫改良土的孔隙度，μ为水的动力粘度，γ为水的容重；
[0013]
ξ为折减因子，n是泡沫土的孔隙度，v为水的运动粘度，为泡沫孔隙度。
[0014]
进一步的，泡沫改良土在位置x处水压p
x
下的泡沫有效粒径计算式为：
[0015][0016]
式中：d
10,f
表示泡沫在大气压p下的有效粒径；x用于区分泡沫改良土渗流方向的不同位置，x＝2和x＝1分别对应流入端和流出端，p
x
表示x对应处的水压；d
10,fx
表示泡沫改良土在x对应处水压p
x
下的有效粒径。
[0017]
进一步的，泡沫改良土在位置x处水压p
x
下的泡沫孔隙比计算式为：
[0018][0019]
式中：fer为大气压p下的发泡倍率，x用于区分泡沫改良土渗流方向的不同位置，x＝2和x＝1分别对应流入端和流出端，p
x
表示位置x处的水压；e
fx
为泡沫改良土在位置x处水压p
x
下的泡沫孔隙比。
[0020]
进一步的，在计算泡沫改良土在孔隙比临界值e
fδ
处的渗透系数k
δ
时，首先根据孔隙比临界值e
fδ
得到泡沫改良土在位置δ处的水压p
δ
，然后根据p
δ
确定泡沫改良土在位置δ处的泡沫有效粒径d
10,fδ
；最后根据d
10,fδ
和孔隙比临界值e
fδ
按照公式(01)计算得到泡沫改良土在位置δ处的渗透系数。
[0021]
进一步的，在渗流流入端的泡沫孔隙比或等于小于预设的孔隙比临界值e
fδ
时，泡沫改良土的等效渗透系数k的计算式为：
[0022][0023]
进一步的，渗流流入端的泡沫孔隙比大于预设的孔隙比临界值e
fδ
，且渗流流出端的泡沫孔隙比小于预设的孔隙比临界值e
fδ
时，等效渗透系数k的计算式为：
[0024][0025]
式中：h为泡沫改良土流入端到流出端的距离，s为泡沫改良土流入端至位置δ处的长度；ka为泡沫改良土流入端至位置δ的等效渗透系数，kb为泡沫改良土位置δ至流出端的等效渗透系数，且
[0026]
进一步的，泡沫改良土流入端至位置δ的长度s的计算式为：
[0027][0028]
式中，p2和p1分别为泡沫改良土流入端和流出端的水压，p
δ
为泡沫改良土在位置δ处的水压。
[0029]
进一步的，孔隙比临界值e
fδ
预设为e
fδ
＝0.32。
[0030]
与现有技术相比，本发明具有如下有益效果：
[0031]
本发明无需通过复杂的大型渗透试验，仅通过测量土体和泡沫的有效粒径和孔隙度即可得到泡沫改良土的渗透系数，而且本发明考虑了水压对泡沫改良土中的泡沫的影响，更符合盾构土仓中渣土的实际情况，计算精度相对较高，具有重要的工程指导意义。
附图说明
[0032]
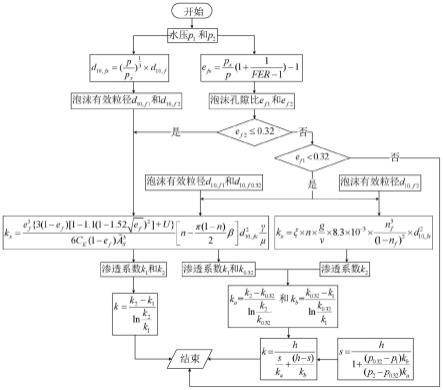
图1为本发明的计算流程图；
[0033]
图2为水压对泡沫改良土初始渗透系数影响机理图；
[0034]
图3为e
f2
≤0.32时泡沫改良土渗透系数变化示意图；
[0035]
图4为e
f2
＞0.32且e
f1
＜0.32时泡沫改良土渗透系数变化示意图。
具体实施方式
[0036]
为使本发明要解决的技术问题、技术方案和优点更加清楚，下面将结合附图及具体实施例进行详细描述。
[0037]
本实施例提供一种考虑水压的泡沫改良土渗透系数计算方法，如图1所示流程图，具体计算步骤如下：
[0038]
s1：确定泡沫改良土渗流方向两端的水压，流入端水压为p2，流出端水压为p1；
[0039]
s2：采用计算水压p1和p2下泡沫的有效粒径d
10,f1
和d
10,f2
；
[0040]
式中：d
10,f
是大气压p下泡沫的有效粒径，d
10,fx
是大气压p
x
下泡沫的有效粒径；
[0041]
s3：采用计算水压p1和p2下泡沫改良土中泡沫的孔隙比e
f1
和e
f2
；
[0042]
式中：e
fx
为水压p
x
下的泡沫孔隙比，fer为大气压p下的发泡倍率；
[0043]
s4：当泡沫孔隙比e
f2
≤0.32时，将泡沫孔隙比e
f1
和d
10,f1
代入如下公式计算流出端的渗透系数k1，将泡沫孔隙比e
f2
和d
10,f2
代入如下公式计算流入端的渗透系数k2，进一步由k1和k2计算泡沫改良土的等效渗透系数k；
[0044][0045]
式中：ck为kozeny常数，为无量纲比表面积，u为无量纲过剩能量密度，为
泡沫相对于土颗粒的细度，d
10,s
为土颗粒的有效粒径，n为泡沫改良土的孔隙度，μ为水的动力粘度，γ为水的容重；
[0046]
s5：当泡沫孔隙比e
f2
＞0.32且e
f1
＜0.32时，将泡沫孔隙比e
f2
和d
10,f2
代入如下公式计算流出端的渗透系数k2：
[0047][0048]
式中：为折减因子，v为水的运动粘度，为泡沫孔隙度；
[0049]
由求出ef＝0.32时泡沫所处的环境压力p
0.32
，并计算此压力下泡沫的有效粒径d
10,f0.32
，将泡沫孔隙比ef＝0.32和d
10,f0.32
代入s4步骤中渗透系数计算公式得到ef＝0.32位置处的渗透系数k
0.32
，将泡沫孔隙比e
f1
和d
10,f1
代入s4步骤中渗透系数计算公式得到流出端的渗透系数k1，进一步由k1、k
0.32
和k2计算泡沫改良土的等效渗透系数。
[0050]
该方法的推导过程如下：
[0051]
考虑水头作用下泡沫改良土的初始渗透系数计算方法，关键在于求解水头作用下改良土中泡沫体积含水率的变化，如图2所示，其中标号1代表泡沫，标号2代表水。通常情况下发泡系统刚发出的泡沫是曝露于大气压中，设大气压为p，此时对应的发泡率为fer，泡沫与土搅拌成泡沫改良土后施加水头进行渗透试验时，此时泡沫所受的外部压力为p
x
，对应的发泡率为fer
x
。
[0052]
泡沫的发泡倍率表达式如下：
[0053][0054]
式中：vf是大气压下泡沫的体积；v
l
是大气压下泡沫液的体积。
[0055]
young-laplace公式形式如下：
[0056][0057]
通常p
外
≥p，而盾构所用泡沫剂的表面张力σ≈37.5mn/m，泡沫的直径r为30～400μm，因此2σ/r p
外
，可认为p
内
≈p
外
。
[0058]
根据boyle定律，气体的体积与气体的压强成反比，存在如下关系：
[0059][0060]
式中：vg是大气压下泡沫内气体的体积；v
gx
是泡沫改良土中泡沫内气体的体积。由于两种外部压力情况下泡沫的总体积vf＝v
fx
，可得：
[0061][0062]
并结合发泡倍率fer的定义，进一步可得：
[0063][0064]
进一步，根据泡沫“孔隙比”ef的定义，可得泡沫改良土中泡沫的“孔隙比”e
fx
为：
[0065][0066]
由于水在泡沫改良土中渗流时水头会有沿程损失，因此泡沫改良土中水压力p
x
沿水的渗流方向呈逐渐减小状态，则泡沫改良土中泡沫的“孔隙比”e
fx
沿水的渗流方向亦呈减小状态。渗流过程中泡沫改良土上端泡沫所承受的水压力最大，渗流通道的过流面积也最大，沿泡沫改良土渗流方向渗透系数逐渐减小。
[0067]
泡沫改良土上端所承受的水压力为p2，泡沫改良土下端所承受的水压力为p1。利用式(6)计算p2对应的改良土内泡沫最大“孔隙比”e
f2
，p1对应的改良土内泡沫最小“孔隙比”e
f1
，并选择相应的分析计算方法。
[0068]
(1)改良土中的泡沫“孔隙比”最大值e
f2
≤0.32
[0069]
此时改良土中的所有泡沫尚未分离，改良土中的泡沫处于稳定的状态，可按照如下所述方法对等效其渗透系数进行计算：
[0070]
①
改良土渗透系数变化函数计算
[0071]
考虑到外水压p
x
发生变化时同样会对泡沫的粒径造成影响，普遍认为有效粒径d
10
是决定多孔介质渗透性的关键粒径。依据young-laplace公式，采用式(7)计算p
x
下泡沫的有效粒径d
10,fx
。
[0072][0073]
将p1、p2下泡沫的有效粒径代入泡沫改良土初始渗透系数计算公式中，可计算出k1与k2。
[0074][0075]
式中：ck为kozeny常数，为无量纲比表面积，u为无量纲过剩能量密度，为泡沫相对于土颗粒的细度，d
10,s
为土颗粒的有效粒径，n为泡沫改良土的孔隙度，μ为水的动力粘度，γ为水的容重；
[0076]
水头沿渗流方向呈线性降低，由于泡沫中渗流通道的过流面积随水压增大而增大，而水压沿渗流方向逐渐减小，则类似地将初始渗透系数沿渗流方向的变化假设为线性变化，如图3所示，其中标号2代表水，标号3代表泡沫改良土，设初始渗透系数ki随渗流路径l的变化关系为ki(l)＝al+b，解得：
[0077][0078]
式中：h为土样高度，k1、k2分别为p1、p2下泡沫改良土对应的渗透系数。
[0079]
②
改良土等效渗透系数计算
[0080]
基于成层土垂直层面渗流等效渗透系数计算公式，提出渗透系数渐变地层垂直渗
流等效渗透系数计算公式，如下：
[0081][0082]
将式(9)带入式(10)，计算得：
[0083][0084]
(2)改良土内泡沫“孔隙比”最大值e
f2
＞0.32且e
f1
＜0.32
[0085]
由于泡沫改良土在渗流过程中水压力沿渗流方向递减，当改良土渗流进口处泡沫的“孔隙比”e
f2
＞0.32且e
f1
＜0.32，则中间必然存在一个临界位置，在该位置以上泡沫“孔隙比”ef大于0.32，以下泡沫“孔隙比”ef小于0.32，假设各部分渗透系数呈线性变化，如图4所示。泡沫改良土初始渗透系数的计算方法如下：
[0086]
①
、改良土渗流进口渗透系数计算
[0087]
在ef＞0.32时，选用针对颗粒物质的kozeny-carmen公式进行分析计算，结合纯土体抗渗理论中颗粒的“粗粒效应”概念，需要在颗粒物质kozeny-carmen公式的基础上乘以泡沫改良土的孔隙度n，然后考虑到土颗粒对泡沫有效渗流通道的折减效应，最终计算式如下：
[0088][0089]
式(13)中，折减因子ξ是泡沫改良土有效渗流通道数s与总渗流通道数s'之比，即v是运动粘度。
[0090]
①
改良土中泡沫e
f2
＝0.32位置深度s计算
[0091]
首先根据e
f2
＝0.32按照式(6)计算此时泡沫所处的环境压力p
0.32
，再进一步根据式(8)计算得到泡沫ef＝0.32时改良土对应的渗透系数k
0.32
，以及泡沫改良土下端泡沫改良土的渗透系数k1。最后利用式(10)分别计算泡沫改良土上端至ef＝0.32段的等效渗透系数ka和ef＝0.32至泡沫改良土下端的等效渗透系数kb，基于流量连续性原理，通过式(13)可求解泡沫改良土上端至ef＝0.32位置的长度s。
[0092][0093]
式中：
[0094]
②
改良土等效渗透系数计算
[0095]
利用成层土垂直层面渗流等效渗透系数计算公式计算整个改良土的等效渗透系数，公式如下：
[0096][0097]
以上实施例为本技术的优选实施例，本领域的普通技术人员还可以在此基础上进行各种变换或改进，在不脱离本技术总的构思的前提下，这些变换或改进都应当属于本技术要求保护的范围之内。