一种加速的牛顿分裂迭代法应用于混合尺寸单元电路布局方法

1.本发明涉及超大规模集成电路物理设计自动化领域，具体涉及一种加速的牛顿分裂迭代法应用于混合尺寸单元电路布局方法。


背景技术：

2.超大规模集成电路(vlsi)电路的物理设计对于半导体芯片的制造至关重要。随着超大规模集成电路先进节点技术的发展，设计具有多种高度的标准单元库的电路成为主流。多倍行高的标准单元具有更好的引脚可达性以及更短的延迟，但是，它们的出现也为布局阶段带来更大的挑战。不同于单倍行高标准单元移动时仅需考虑该行的单元重叠即可，多倍行高单元的移动过程中，还需额外考虑相邻行单元的重叠问题。除此之外，混合尺寸单元的布局还需遵循电源轨匹配的限制。电路设计中标准单元的数量巨大，使得解空间组合爆炸，具有极高的计算复杂度，因此布局问题是一个np-难问题。对于该类问题，通常采用迭代求解的方法来获得近似解，如何快速、高效地逼近最优解是当前亟待解决的一个问题。
3.现有的合法化算法分为启发式算法和解析式算法；启发式算法具有求解速度快的优点，然而容易陷入局部最优解。解析式方法通常对合法化问题建立一个数学模型，从而对该模型进行求解。陈建利等(cn106971042a)提出了将合法化问题中的二次规划问题等价地表示为线性互补问题，并应用模系矩阵分裂迭代法对线性互补问题进行求解，然而该方法需要确定较多参数，如果其中一个参数选取不当，则容易造成迭代方法无法收敛。


技术实现要素：

4.发明目的：本发明的目的是为了解决上述问题，通过将与合法化问题等价的线性互补问题转化成一个广义绝对值方程，然后设计了一种加速的牛顿分裂迭代法进行求解。与现有方法相比，仅包含一个参数矩阵，且对该参数矩阵的选取给出了建议，有效避免了因参数选择不当而造成难以收敛或者收敛速度过慢的问题。该发明能大大减少迭代求解过程中的迭代次数以及运行时间，进一步提升布局阶段的设计效率。
5.加速的牛顿分裂迭代法应用于混合尺寸单元电路布局方法：首先对多倍行高单元预处理成单倍行高子单元，并放置到最近的与电源线匹配的行上，然后对所有单元建立网络流模型，对其进行扩散，避免局部拥挤，接着将合法化问题表述为一个凸二次规划问题，并将二次规划问题等价地转换成线性互补问题，然后将线性互补问题等价地表示成广义绝对值方程，设计了一种加速的牛顿分裂迭代法求解，最后将多倍行高标准单元进行复原并放置到行中的可放置位上，并对余下的非法单元进行处理。与现有技术相比，本发明通过加速的牛顿分裂迭代法对与合法化问题等价的广义绝对值方程进行求解，无需过多考虑参数的设置，仅需确定一个参数矩阵，且对该参数矩阵的选取给出建议，避免了因参数或参数矩阵的选取不当而无法有效或高效求解的局限；能够有效加快迭代过程的收敛速度，并快速得到合法化问题的高质量邻域解。
6.为了实现以上目的，本发明提供一种加速的牛顿分裂迭代法应用于混合尺寸单元电路布局方法，包括如下步骤：
7.s1：对标准单元进行预处理，将多倍行高标准单元分割为多个单倍行高标准子单元，并放置到最近的与电源线匹配的行上；
8.s2：对所有单元建立网络流模型，对其进行扩散；
9.s3：将合法化问题表述为一个凸二次规划问题；
10.s4：将二次规划问题等价地转换成线性互补问题；
11.s5：将线性互补问题等价地表示成广义绝对值方程；
12.s6：利用加速的牛顿迭代法求解广义绝对值方程；
13.s7：将多倍行高标准单元进行复原并放置到行中的可放置位上；
14.s8：对剩余的非法单元进行合法化处理。
15.进一步的，步骤s1的具体实现方式包括：给定一个芯片的矩形布局区域，用(0，0)和(w，h)分别表示其左下角坐标和右上角坐标；w表示布局区域的宽度，h表示布局区域的高度；待布局的可移动标准单元集为c＝(c1，c2，
…cn
)，其中单元ci从全局阶段获得的初始左下角坐标为单元宽度及高度分别为wi，hi，所求的合法化阶段后的坐标用(xi，yi)表示；对于多倍行高标准单元，将其表示成多个子单元，用(c
i1
，c
i2
，
…cit
)表示，其中，t表示标准单元的高度是行高的t倍。
16.进一步的，所有单元的高度都是行高的整数倍；然后将所有标准单元对齐到最近的与其电源线匹配的行上去；电源线和接地线在行中交错排布，对于奇数倍行高单元，其两端的电源类型是不同的，因此只要不超出布局区域，便可以放置在任意的行上面，通过翻转来实现电源类型的匹配；对于偶数倍行高单元，其两端的电源类型是相同的，因此需要放置到与其电源类型匹配的行上。
17.进一步的，步骤s2的具体实现方式包括：为避免后续处理中标准单元过于拥挤，利用网络流算法对单元进行扩散，确保每行中的单元宽度之和不超过该行的宽度，对布局区域在水平方向和垂直方向进行均匀地划分成网格，每一个网格构成网络流图中的一个节点，此外，再额外创建两个节点，即超级源节点(nb)和超级汇节点(ne)，计算每个网格中所属单元的面积之和sc，将其与网格面积sg进行比较，如果sc＞sg，则该网格称为溢出网格并记录溢出的面积so，如果sc≤sg，则该网格称为空闲网格并记录剩余的空闲面积sf，对于溢出网格，将其设置成网络流中的源节点ns，并建立一条从nb到ns的弧，弧上的容量和成本分别设置为so和零，对于空闲网格，将其设置为目标节点n
t
，并建立一条从n
t
到ne的弧，弧上的容量和成本分别设置为sf和0，并且对溢出网格，寻找与它相邻的空闲网格，建立从ns到n
t
的弧，弧上的容量和成本分别设置为无穷大和单元在两个网格之间移动的位移，对于建立好的网络流图进行求解，可得到单元在网格中移动的策略，按照该策略移动单元，移动后的单元ci的坐标为进一步的，步骤s3的具体实现方式包括：合法化过程是消除单元之间的重叠，并以最小化标准单元总位移为优化目标，并且在前述步骤中单元已经进行垂直方向上的最小移动，即与匹配的电源轨对齐，因此可忽略垂直方向上的位移，将合法化问题描述为下述模型(27)：
[0018][0019]
将上述模型改写为凸二次规划问题的标准形式，即：
[0020][0021]
其中，是一个单位矩阵，是一个列向量，其分量由标准单元的初始横坐标构成；任意相邻的一对标准单元应该满足不等式x
j-xi≥wi(xj≥xi)，对所有相邻单元之间建立该不等式，则可以写成矩阵形式wx≥d，w为每行仅包含-1和1这两个元素的矩阵，分别表示单元ci和cj的横坐标xj，xi，d为一个列向量，其中对应的分量表示左侧单元ci的宽度wi；那么w和d的行数为约束的个数，w的列数为标准单元的总个数，即单倍行高单元的数量与多倍行高单元拆分成的子单元数量之和，则单倍行高单元的数量与多倍行高单元拆分成的子单元数量之和，则r同样为每行由-1和1组成的矩阵，-1表示多倍行高单元ci的子单元c
i1
，1表示ci的子单元c
i2
，依次推类；x
i2-x
i1
＝0保证ci的子单元横坐标相等，由此可得到约束矩阵rx＝0，其中根据该位置构造的矩阵w、r和向量d如下所示：
[0022]
r＝(0
ꢀ‑
1 1 0)，d＝(w
1 w2)
t
；
[0023]
利用拉格朗日乘子法，将二次规划中的等式约束加入到目标函数中，则(2)可表示为：
[0024][0025]
其中，λ为拉格朗日乘子。
[0026]
进一步的，所述步骤s4的具体实施方式为：利用karush-kuhn-tucker(kkt)条件，可将模型(3)写成如下条件的kkt方程组：
[0027][0028]
将方程组(4)改下为如下形式：
[0029][0030]
令该问题则演变为寻求一对非负且正交的解向量
[0031]
满足如下条件：
[0032]
w＝az+q≥0，z≥0 and w
t
z≥0.
ꢀꢀꢀꢀ
(19)
[0033]
问题(6)则为线性互补问题，其中
[0034]
进一步的，所述步骤s5的具体实施方式为：令z＝(|v|-v)，w＝(|v|+v)，则(6)可转换成下列等价的广义绝对值方程：
[0035]
(a+i)v-(a-i)|v|＝q.
ꢀꢀꢀꢀꢀ
(20)
[0036]
令c＝a+i，e＝a-i，其中i为单位矩阵，则(7)可重新表述为如下形式：
[0037]
cv-e|v|＝q.
ꢀꢀꢀꢀ
(21)。
[0038]
进一步的，所述步骤s6的具体实施方式为：令f(v)＝cv-e|v|-q，并令f(v)＝0；由于f(v)是一个分段线性向量函数，不是连续可微的，不能直接应用牛顿迭代方法来求解此方程；因此，基于|v|的分量的次梯度，使用|v|的广义雅可比来获得广义绝对值方程(8)的近似解；可用对角矩阵d(v)表示，其中且sign(vk)为一个向量，其分量值为
[0039][0040]
对于非线性等式系统f(v)，将其分解为可微函数h(v)与lipschitz连续函数g(v)之和，即f(v)＝h(v)+g(v)，因此可以利用一种修正的牛顿迭代法求解f(v)，即
[0041]vk+1
＝v
k-h
′
(vk)-1
(h(vk)+g(vk))，k＝0，1，2，
…
，
ꢀꢀꢀꢀ
(23)
[0042]
取h(v)＝c(v)+ω(v)，g(v)＝-ω(v)-e|v|-q，其中ω为半正定矩阵，利用(10)求解f(v)可得到如下迭代格式：
[0043]vk+1
＝v
k-(c+ω)-1
(cv
k-e|vk|-q).
ꢀꢀꢀꢀ
(24)
[0044]
将(11)两边同时乘以(c+ω)可得
[0045]
(c+ω)v
k+1
＝ωvk+e|vk|+g.
ꢀꢀꢀꢀ
(25)
[0046]
由于c＝a+i，e＝a-i，因此矩阵c和e是两个正定矩阵，令c＝m
1-n1为矩阵c的分裂，e＝m
2-n2为矩阵e的分裂，并将最新的估计值v
k+1
替换等式右侧的vk，可得到如下迭代格式：
[0047]
(m1+ω)v
k+1
＝(n1+ω)vk+m2|vk|-n2|v
k+1
|+q.
ꢀꢀꢀꢀ
(26)
[0048]
其中，要求n2是一个下三角矩阵；具体地，根据式(5)中矩阵a的结构，将m1，n1，m2，n2取值如下：
[0049][0050][0051]
其中，为单位矩阵；取ω＝ωi，ω为正常数，令b1＝b+λr
t
r，因此，利用式(13)求解合法化问题的过程如下所示：
[0052][0053]
给定一个任意的初始向量通过迭代地求解线性系统来计算v
k+1
的值，直到绝对残差向量的二范数res(vk)：＝||z
k-z
k-1
||2小于等于给定的一个常数，此时可认为迭代序列收敛，且zk＝(|vk|-vk)，k＝0，1，2，
…
。
[0054]
进一步的，所述步骤s7的具体实施方式为：将所求得的每个多倍行高标准单元的所有子单元的坐标按照升序排序，中位数即为所求的该多倍行高单元的坐标，接着将单元放置到离所求得的坐标最近的可放置位上。
[0055]
进一步的，所述步骤s8的具体实施方式为：针对少许仍然重叠或超出布局区域右边界的标准单元，从布局区域右上角开始，按照从右到左，从上到下的顺序对标准单元进行遍历，若单元ci超过右边界，则把其坐标置为w-wi，若单元ci与c
i-1
重叠，则将c
i-1
坐标置为x
i-w
i-1
；由于多倍行高单元的移动可能会引起相邻行的单元重叠，因此，对于在上一行中已经移动过的多倍行高单元，在下一行则不再移动它们；接着，按照相同的规则从左到右，从下到上的顺序遍历再次遍历标准单元，经过该步骤处理后，所有单元重叠均可消除。
[0056]
本发明的上述技术方案相比现有技术具有以下优点：首先对多倍行高单元预处理成单倍行高子单元，并放置到最近的与电源线匹配的行上，然后对所有单元建立网络流模型，对其进行扩散，避免局部拥挤，接着将合法化问题表述为一个凸二次规划问题，并将二次规划问题等价地转换成线性互补问题，然后将线性互补问题等价地表示成广义绝对值方程，设计了一种加速的牛顿分裂迭代法求解，最后将多倍行高标准单元进行复原并放置到行中的可放置位上，并对余下的非法单元进行处理。与现有技术相比，本发明通过加速的牛顿分裂迭代法对与合法化问题等价的广义绝对值方程进行求解，无需过多考虑参数的设置，仅需确定一个参数矩阵，且对该参数矩阵的选取给出建议，避免了因参数或参数矩阵的选取不当而无法有效或高效求解的局限。能够有效加快迭代过程的收敛速度，并快速得到合法化问题的高质量邻域解。
[0057]
与现有技术相比，本发明通过将与合法化问题等价的线性互补问题转化成一个广义绝对值方程，然后设计了一种加速的牛顿分裂迭代法进行求解。与现有方法相比，本发明仅包含一个参数矩阵，且对该参数矩阵的选取给出了建议，有效避免了因参数选择不当而造成难以收敛或者收敛速度过慢的问题。该发明能大大减少迭代求解过程中的迭代次数以及运行时间，进一步提升布局阶段的设计效率。
附图说明
[0058]
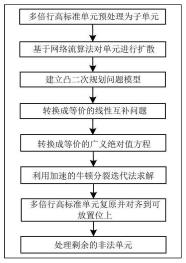
图1是混合尺寸标准单元电路合法化流程图；
[0059]
图2是考虑电源轨约束的布局说明图；
[0060]
图3是混合尺寸标准单元的布局示例图
[0061]
图4是加速的牛顿迭代法求解步骤图；
[0062]
图5是加速的牛顿迭代法求解由合法化问题导出的广义绝对值方程的一个实施例迭代图。
具体实施方式
[0063]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅是本发明一部分实施例，而不是全部的实施例，基于本发明中的实施例，本领域技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0064]
如图1所示，一种加速的牛顿分裂迭代法应用于混合尺寸单元电路布局方法，具体包括如下步骤：
[0065]
s1：对标准单元进行预处理，将多倍行高标准单元分割为多个单倍行高标准子单元，并放置到最近的与电源线匹配的行上；
[0066]
s2：对所有单元建立网络流模型，对其进行扩散；
[0067]
s3：将合法化问题表述为一个凸二次规划问题；
[0068]
s4：将二次规划问题等价地转换成线性互补问题；
[0069]
s5：将线性互补问题等价地表示成广义绝对值方程；
[0070]
s6：利用加速的牛顿迭代法求解广义绝对值方程；
[0071]
s7：将多倍行高标准单元进行复原并放置到行中的可放置位上；
[0072]
s8：对剩余的非法单元进行合法化处理。
[0073]
本实例中进一步地，步骤s1的具体实现方式包括：给定一个芯片的矩形布局区域，用(0，0)和(w，h)分别表示其左下角坐标和右上角坐标；w表示布局区域的宽度，h表示布局区域的高度；待布局的可移动标准单元集为c＝(c1，c2，
…cn
)，其中单元ci从全局阶段获得的初始左下角坐标为单元宽度及高度分别为wi，hi，所求的合法化阶段后的坐标用(xi，yi)表示；对于多倍行高标准单元，将其表示成多个子单元，用(c
i1
，c
i2
，
…cit
)表示，其中，t表示标准单元的高度是行高的t倍；注意，所有单元的高度都是行高的整数倍；然后将所有标准单元对齐到最近的与其电源线匹配的行上去；电源线和接地线在行中交错排布；对于奇数倍行高单元，其两端的电源类型是不同的，因此只要不超出布局区域，便可以放置在任意的行上面，通过翻转来实现电源类型的匹配；对于偶数倍行高单元，其两端的电源类型是相同的，因此需要放置到与其电源类型匹配的行上；如图2所示，红线代表电源线，蓝线代表接地线，虚线表示单元可以放置的行。
[0074]
本实例中进一步地，步骤s2的具体实现方式包括：为避免后续处理中标准单元过于拥挤，利用网络流算法对单元进行扩散，确保每行中的单元宽度之和不超过该行的宽度；我们对布局区域在水平方向和垂直方向进行均匀地划分成网格，每一个网格构成网络流图中的一个节点；此外，再额外创建两个节点，即超级源节点(nb)和超级汇节点(ne)；计算每个网格中所属单元的面积之和sc，将其与网格面积sg进行比较；如果sc＞sg，则该网格称为溢出网格并记录溢出的面积so；如果sc≤sg，则该网格称为空闲网格并记录剩余的空闲面积sf；对于溢出网格，将其设置成网络流中的源节点ns，并建立一条从nb到ns的弧，弧上的容量和成本分别设置为so和零；对于空闲网格，将其设置为目标节点n
t
，并建立一条从n
t
到ne的弧，弧上的容量和成本分别设置为sf和0；并且对溢出网格，寻找与它相邻的空闲网格，建立从ns到n
t
的弧，弧上的容量和成本分别设置为无穷大和单元在两个网格之间移动的位移；对于建立好的网络流图进行求解，可得到单元在网格中移动的策略，按照该策略移动单元，移动后的单元ci的坐标为
[0075]
本实例中进一步地，步骤s3的具体实现方式包括：合法化过程是消除单元之间的重叠，并以最小化标准单元总位移为优化目标，并且在前述步骤中单元已经进行垂直方向上的最小移动，即与匹配的电源轨对齐，因此可忽略垂直方向上的位移，将合法化问题描述为下述模型(27)：
[0076][0077]
将上述模型改写为凸二次规划问题的标准形式，即：
[0078][0079]
其中，是一个单位矩阵，是一个列向量，其分量由标准单元的初始横坐标构成；任意相邻的一对标准单元应该满足不等式x
j-xi≥wi(xj≥xi)，对所有相邻单元之间建立该不等式，则可以写成矩阵形式wx≥d，w为每行仅包含-1和1这两个元素的矩阵，分别表示单元ci和cj的横坐标xj，xi，d为一个列向量，其中对应的分量表示左侧单元ci的宽度wi；那么w和d的行数为约束的个数，w的列数为标准单元的总个数，即单倍行高单元的数量与多倍行高单元拆分成的子单元数量之和，则单倍行高单元的数量与多倍行高单元拆分成的子单元数量之和，则r同样为每行由-1和1组成的矩阵，-1表示多倍行高单元ci的子单元c
i1
，1表示ci的子单元c
i2
，依次推类；x
i2-x
i1
＝0保证ci的子单元横坐标相等，由此可得到约束矩阵rx＝0，其中图3是一个混合尺寸标准单元布局的简单示例图，根据该位置构造的矩阵w、r和向量d如下所示：
[0080]
r＝(0
ꢀ‑
1 1 0)，d＝(w
1 w2)
t
；
[0081]
利用拉格朗日乘子法，将二次规划中的等式约束加入到目标函数中，则(2)可表示为：
[0082][0083]
其中，λ为拉格朗日乘子。
[0084]
本实例中进一步地，所述步骤s4的具体实施方式为：利用karush-kuhn-tucker(kkt)条件，可将模型(3)写成如下条件的kkt方程组：
[0085][0086]
将方程组(4)改下为如下形式：
[0087][0088]
令该问题则演变为寻求一对非负且正交的解向量满足如下条件：
[0089]
w＝az+q≥0，z≥0 and w
t
z≥0.
ꢀꢀꢀꢀ
(32)
[0090]
问题(6)则为线性互补问题，其中
[0091]
本实例中进一步地，所述步骤s5的具体实施方式为：令z＝(|v|-v)，w＝(|v|+v)，则(6)可转换成下列等价的广义绝对值方程：
[0092]
(a+i)v-(a-i)|v|＝q.
ꢀꢀꢀꢀ
(33)
[0093]
令c＝a+i，e＝a-i，其中i为单位矩阵，则(7)可重新表述为如下形式：
[0094]
cv-e|v|＝q.
ꢀꢀꢀꢀ
(34)
[0095]
本实例中进一步地，所述步骤s6的具体实施方式为：令f(v)＝cv-e|v|-q，并令f(v)＝0；由于f(v)是一个分段线性向量函数，不是连续可微的，不能直接应用牛顿迭代方法来求解此方程；因此，基于|v|的分量的次梯度，使用|v|的广义雅可比来获得广义绝对值方程(8)的近似解；可用对角矩阵d(v)表示，其中且sign(vk)为一个向量，其分量值为
[0096][0097]
对于非线性等式系统f(v)，将其分解为可微函数h(v)与lipschitz连续函数g(v)之和，即f(v)＝h(v)+g(v)，因此可以利用一种修正的牛顿迭代法求解f(v)，即
[0098]vk+1
＝v
k-h
′
(vk)-1
(h(vk)+g(vk))，k＝0，1，2，
…
，
ꢀꢀꢀꢀ
(36)
[0099]
根据论文广义绝对值方程的修正牛顿型迭代法，取h(v)＝c(v)+ω(v)，g(v)＝-ω(v)-e|v|-q，其中ω为半正定矩阵，利用(10)求解f(v)可得到如下迭代格式：
[0100]vk+1
＝v
k-(c+ω)-1
(cv
k-e|vk|-q).
ꢀꢀꢀꢀ
(37)
[0101]
将(11)两边同时乘以(c+ω)可得
[0102]
(c+ω)v
k+1
＝ωvk+e|vk|+q.
ꢀꢀꢀꢀ
(38)
[0103]
由于c＝a+i，e＝a-i，因此矩阵c和e是两个正定矩阵，本发明中令c＝m
1-n1为矩阵c的分裂，e＝m
2-n2为矩阵e的分裂，并将最新的估计值v
k+1
替换等式右侧的vk，可得到如下迭代格式：
[0104]
(m1+ω)v
k+1
＝(n1+ω)vk+m2|vk|-n2|v
k+1
|+q.
ꢀꢀꢀꢀ
(39)
[0105]
其中，要求n2是一个下三角矩阵；具体地，根据式(5)中矩阵a的结构，将m1，n1，m2，n2取值如下：
[0106][0107]
[0108]
其中，为单位矩阵；取ω＝ωi，ω为正常数，令b1＝b+λr
t
r，因此，利用式(13)求解合法化问题的过程如下所示：
[0109][0110]
给定一个任意的初始向量通过迭代地求解线性系统来计算v
k+1
的值，直到绝对残差向量的二范数res(vk)：＝||z
k-z
k-1
||2小于等于给定的一个常数，此时可认为迭代序列收敛，且zk＝(|vk|-vk)，k＝0，1，2，
…
；求解流程如图4所示；图5给出了将一个合法化问题转化成广义绝对值方程后，应用加速的牛顿分裂迭代法求解的一个实施例，横坐标表示迭代次数，纵坐标表示绝对残差向量的二范数res的值，迭代收敛条件为res(v
(k)
)≤10-5
。
[0111]
本实例中进一步地，所述步骤s7的具体实施方式为：将所求得的每个多倍行高标准单元的所有子单元的x坐标按照升序排序，中位数即为所求的该多倍行高单元的x坐标，接着将单元放置到离所求得的x坐标最近的可放置位上。
[0112]
本实例中进一步地，所述步骤s8的具体实施方式为：针对少许仍然重叠或超出布局区域右边界的标准单元，从布局区域右上角开始，按照从右到左，从上到下的顺序对标准单元进行遍历，若单元ci超过右边界，则把其坐标置为w-wi，若单元ci与c
i-1
重叠，则将c
i-1
坐标置为x
i-w
i-1
；由于多倍行高单元的移动可能会引起相邻行的单元重叠，因此，对于在上一行中已经移动过的多倍行高单元，在下一行则不再移动它们；接着，按照相同的规则从左到右，从下到上的顺序遍历再次遍历标准单元，经过该步骤处理后，所有单元重叠均可消除。
[0113]
上述中论文广义绝对值方程的修正牛顿型迭代法，具体论文信息：wang a，caoy，chen j x.modified newton-type iteration methods for generalized absolute value equations[j].journal of optimization theory andapplications，2019，181(1)：216-230。
[0114]
以上所述仅为本发明的示例性实施例，并非因此限制本发明专利保护范围，凡是利用本发明说明书及附图内容所作的等效结构或等效流程变换，或直接或间接运用在其他相关的技术领域，均同理包括在本发明的专利保护范围内。