基于人工神经网络的有限元数值模拟后验误差估计方法与流程

1.本发明涉及有限元数值解的后验误差估计方法，具体涉及一种基于人工神经网络的静电场泊松方程有限元数值模拟后验误差估计方法。


背景技术：

2.有限元方法是当前数值模拟技术中一种重要的方法，其在物理和工程上的偏微分方程数值求解中发挥着重要作用。有限元方法的基本思想是对计算区域进行网格剖分，在每个网格上构造一个分片函数(多项式)，然后结合变分原理求解得到物理问题的数学模型(通常表现为一组偏微分方程及初边值条件)的近似解，其实质是用有限维空间的离散解来逼近无穷维空间的连续解。由于有限元方法本质上是对物理模型的近似求解，因此近似解必然存在一定的误差(与数学模型的真解存在一定的差异)。误差的大小，决定了有限元数值解的可靠性和应用价值。对于静电场问题，当采用有限元方法求解其泊松方程时，所求得的数值解的准确性对于静电场问题分析具有重要影响。有限元后验误差估计方法能够量化评价泊松方程有限元数值解的准确性，从而为静电场问题分析结果的正确性提供支撑。
3.随着有限元方法理论的不断发展，逐渐建立了有限元方法的后验误差估计理论，并产生了多种后验误差估计方法，包括残量型估计、局部问题辅助型估计、分级型估计、重构型估计等。有限元后验误差估计方法能够对有限元数值解的误差给出量化估计，从而能够用于量化评价数值解的准确性。但是上述的后验误差估计方法，针对不同有限元网格类型，需要从方法上做不同的方法设计，从算法和程序两个方面来看都较为复杂。


技术实现要素：

4.本发明的目的是解决现有静电场泊松方程有限元数值解后验误差估计方法针对不同有限元网格类型，需要从方法上做不同的方法设计，导致算法和程序的复杂度较高的不足之处，而提供一种基于人工神经网络的有限元数值模拟后验误差估计方法。
5.为了解决上述现有技术所存在的不足之处，本发明提供了如下技术解决方案：
6.一种基于人工神经网络的有限元数值模拟后验误差估计方法，其特殊之处在于，包括如下步骤：
7.步骤1、在静电场的分析区域ω计算有限元数值解；
8.步骤1.1、确定静电场的分析区域ω并测量，然后测定分析区域的电荷密度、分析区域边界处的电势值；建立静电场泊松方程
9.步骤1.2、应用有限元方法求解静电场泊松方程；
10.将静电场泊松方程的分析区域ω作为计算区域ω进行剖分得到网格单元k的集合th，定义其表示在集合th中任意单元k上的次数不超过k的多项式函数空间，则在函数空间vh中存在有限元数值解uh，使得uh满足方程其中其中
11.其中，u为未知电势函数，v为多项式函数，l2(ω)为在ω内所有平方可积的函数组成的函数空间，为sobolev空间，表示电荷密度，ε0＝8.854
×
10-12
f/m表示介电常数，(
·
,
·
)表示函数内积；
12.步骤2、构建神经网络模型；
13.在步骤1所确定的计算区域ω的内部和边界上取点，记为其中d表示区域ω的维数；n是所取的点数目；
14.采用pytorch软件包构建神经网络模型，所述神经网络模型的第一层为输入层，输入层的输入数据为输入层的维数为d；神经网络模型的最后一层为输出层，输出层的维数为d；输入层和输出层之间设置有l个隐藏层，各隐藏层有m
l
个神经元，l＝1,2,
…
,l；
15.根据各隐藏层的神经元间的连接权重和每个神经元的激活水平计算各隐藏层的神经元输出；
16.步骤3、根据泊松方程及其有限元数值解定义神经网络模型的损失函数，通过pytorch软件包采用随机梯度下降算法训练神经网络模型；
17.步骤4、通过步骤3所得的神经网络模型计算泊松方程有限元数值解在区域ω上的后验误差。
18.进一步地，步骤2中，所述神经网络模型的第l个隐藏层的神经元输出为：
19.当l＝1，
20.其中，为第1个隐藏层中第k个神经元输出，是输入层第i2个输入到第1个隐藏层的第k个神经元的连接权重，是第1个隐藏层中第k个神经元的激活水平，m1为第1个隐藏层的神经元个数；神经元激活函数元个数；神经元激活函数
21.当l＝2,
…
,l，
22.其中，为第l隐藏层的第k个神经元输出，为第l-1隐藏层中第i2个神经元输出，是第l-1个隐藏层中第o2个神经元输出到第l个隐藏层的第k个神经元的连接权重，是第l个隐藏层中第k个神经元的激活水平，m
l
为第l个隐藏层的神经元个数；
23.输出层的神经元输出为：
[0024][0025]
其中，是第l隐藏层中第i2个神经元输出到输出层第k个神经元的连接权重，
是输出层第k个神经元的激活水平。
[0026]
进一步地，步骤3中，所述神经网络模型的损失函数为：
[0027][0028]
其中，β1和β2是两个权重系数；net(x)为神经网络模型；uh表示有限元数值解；是有限元数值解的梯度；f(x)表示泊松方程的右端项；是的散度；采用数值积分的方法计算
[0029]
进一步地，所述步骤4具体为：
[0030][0031][0032]
其中，∈k为有限元数值解在每个网格上的局部误差，∈是有限元数值解在区域ω上的后验误差；
[0033]
有限元数值解uh和未知真解u的能量误差有下式成立：
[0034][0035]
是未知真解u的梯度。
[0036]
进一步地，步骤2中，所述取点的规则可以是随机取点，也可以是对区域ω进行网格剖分，获得的结构网格或非结构网格的节点，用于保证所取节点对区域ω的内部和边界都具有代表性。
[0037]
与现有技术相比，本发明的有益效果是：
[0038]
(1)本发明一种基于人工神经网络的有限元数值模拟后验误差估计方法根据静电场泊松方程采用pytorch软件包构建神经网络模型，通过神经网络模型完成神经网络训练后，即可用于估计不同网格下有限元数值解的后验误差，而不需要重新训练神经网络。特别是将后验误差仅用于网格自适应算法的情况，与经典后验误差估计方法相比，本发明由于省去了构造后验误差的过程，从而节省了计算量；
[0039]
根据本发明给出的后验误差结果，结合可接受的误差限，可以确定是否需要进一步加密网格重新进行静电场泊松方程有限元分析计算过程，进而提高静电场泊松方程的求解精度；此外，可以将本发明给出的后验误差结果用于静电场泊松方程有限元自适应分析中网格自适应算法中的网格指示子。
[0040]
(2)本发明一种基于人工神经网络的有限元数值模拟后验误差估计方法是一种无网格方法，对有限元网格没有要求，同时适用于二维三角形/四边形和三维四面体/六面体等常用网格。
附图说明
[0041]
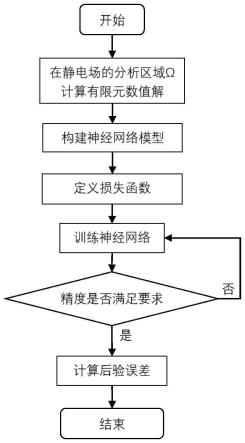
图1为本发明一种基于人工神经网络的有限元数值模拟后验误差估计方法的流程示意图；
[0042]
图2为本发明步骤1在计算区域ω取点的示意图；
[0043]
图3为本发明步骤2所构建的神经网络模型的结构示意图；
[0044]
图4为实施例一泊松方程解析解的曲面图；
[0045]
图5为实施例一、实施例四计算数值解使用的网格；
[0046]
图6为实施例一泊松方程数值解的曲面图；
[0047]
图7为实施例一步骤3神经网络训练20000步损失函数的收敛情况；
[0048]
图8为实施例一真实误差∈
*
的分布图；
[0049]
图9为实施例一后验误差∈的分布图；
[0050]
图10为实施例二真实误差∈
*
的分布图；
[0051]
图11为实施例二后验误差∈的分布图；
[0052]
图12为实施例三真实误差∈
*
的分布图；
[0053]
图13为实施例三后验误差∈的分布图；
[0054]
图14为实施例四泊松方程解析解的曲面图；
[0055]
图15为实施例四泊松方程数值解的曲面图；
[0056]
图16为实施例四步骤3神经网络训练20000步损失函数的收敛情况；
[0057]
图17为实施例四真实误差∈
*
的分布图；
[0058]
图18为实施例四后验误差∈的分布图；
[0059]
图19为实施例五真实误差∈
*
的分布图；
[0060]
图20为实施例五后验误差∈的分布图；
[0061]
图21为实施例六真实误差∈
*
的分布图；
[0062]
图22为实施例六后验误差∈的分布图。
具体实施方式
[0063]
下面结合附图和示例性实施例对本发明作进一步地说明。
[0064]
实施例一
[0065]
参照图1，一种基于人工神经网络技术的有限元数值模拟后验误差估计方法，包括如下步骤：
[0066]
步骤1、在静电场的分析区域ω计算有限元数值解；
[0067]
步骤1.1、确定静电场的分析区域ω并测量，然后测定分析区域的电荷密度、分析区域边界处的电势值；
[0068]
本实施例中，分析区域为ω＝[0,1]
×
[0,1]，在分析区域边界处的电势值为0，分析区域的电荷密度为(库伦/平方米)；
[0069]
建立静电场泊松方程：
[0070]-δu＝8π2sin(2πx)sin(2πy)
[0071]
u|
γ
＝0
[0072]
得到解析解u＝sin(2πx)sin(2πy)，如图4所示；
[0073]
步骤1.2、根据解析解u，应用有限元方法求解静电场泊松方程：
[0074]
将静电场泊松方程的分析区域ω作为计算区域ω进行剖分得到网格单元k的集合th，定义pk(k)表示在集合th中任意单元k上的次数不超过k的多项式函数空间，则在函数空间vh中存在有限元数值解uh，使得uh满足方程其中其中
[0075]
其中，u为未知电势函数，v为多项式函数，l2(ω)为在ω内所有平方可积的函数组成的函数空间，l2(ω)为在ω内所有平方可积的函数组成的函数空间，为sobolev空间，ε0＝8.854
×
10-12
f/m表示介电常数；
[0076]
根据解析解u，应用有限元方法计算得到有限元数值解uh；图5是计算数值解uh使用的网格，网格数为224；图6是泊松方程数值解uh的曲面图；
[0077]
步骤2、采用pytorch软件包构建神经网络模型；
[0078]
参照图2，在步骤1所确定的计算区域ω的内部和边界上取点，记为其中d表示区域ω的维数；n是所取的点数目；
[0079]
所述取点的规则可以是随机取点，也可以是对区域ω进行网格剖分，获得的结构网格或非结构网格的节点，用于保证所取节点对区域ω的内部和边界都具有代表性；
[0080]
参照图3，所述神经网络模型的第一层为输入层，输入层的输入数据为输入层的维数为d；神经网络模型的最后一层为输出层，输出层的维数为d；输入层和输出层之间设置有l个隐藏层，各隐藏层有m
l
个神经元，l＝1,2,
…
,l；
[0081]
根据各隐藏层的神经元间的连接权重和每个神经元的激活水平计算各隐藏层的神经元输出；
[0082]
所述神经网络模型的第l个隐藏层的神经元输出为：
[0083]
当l＝1，
[0084]
其中，为第1个隐藏层中第k个神经元输出，是输入层第i2个输入到第1个隐藏层的第k个神经元的连接权重，是第1个隐藏层中第k个神经元的激活水平，m1为第1个隐藏层的神经元个数；神经元激活函数个隐藏层的神经元个数；神经元激活函数
[0085]
向量形式为：
[0086][0087]
其中，为第l隐藏层的第k个神经元输出，为第l-1隐藏层中第i2个神经元输出，是第l-1个隐藏层中第i2个神经元输出到第l个隐藏层的第k个神经元的连接权重，是第l个隐藏层中第k个神经元的激活水平，m
l
为第l个隐藏层的神经元个数；
[0088]
输出层的神经元输出为：
[0089][0090]
向量形式为：
[0091][0092]
其中，是第l隐藏层中第i2个神经元输出到输出层第k个神经元的连接权重，是输出层第k个神经元的激活水平；
[0093]
步骤3、根据泊松方程及其有限元数值解定义神经网络模型的损失函数，通过pytorch软件包采用随机梯度下降算法训练神经网络模型；
[0094]
所述神经网络模型的损失函数为：
[0095][0096]
其中，β1和β2是两个权重系数；net(x)为神经网络模型；uh表示有限元数值解；是有限元数值解的梯度；f(x)表示泊松方程的右端项；是的散度；
[0097]
采用数值积分的方法计算
[0098]
图7为本实施例神经网络训练20000步损失函数的收敛情况；
[0099]
步骤4、
[0100][0101][0102]
其中，∈k为有限元数值解在每个网格上的局部误差，∈是有限元数值解在区域ω上的后验误差；
[0103]
有限元数值解uh和未知真解u的能量误差有下式成立：
[0104][0105]
是未知真解u的梯度。
[0106]
图8为真实误差∈
*
的分布图，图9为本实施例所得的后验误差∈的分布图。可以看出，本发明准确的估计了真实误差的分布图情况。
[0107]
实施例二
[0108]
本实施例应用实施例一相同泊松方程算例，计算数值解uh所使用网格的网格数为56，不重新训练神经网络，其余设置均与实施例一相同。
[0109]
图10为真实误差∈
*
的分布图，图11为本实施例所得的后验误差∈的分布图。
[0110]
实施例三
[0111]
本实施例应用实施例一相同泊松方程算例，计算数值解uh所使用网格的网格数为896，不重新训练神经网络，其余设置均与实施例一相同。
[0112]
图12为真实误差∈
*
的分布图，图13为本实施例所得的后验误差∈的分布图。
[0113]
表1给出了实施例一至三的真实误差∈
*
与后验误差∈，结果表明本发明可以用于估计数值解的真实误差。
[0114]
表1
[0115]
实施例网格数真实误差后验误差是否训练网络一2241.0641.105是二562.0892.109否三8960.5360.615否
[0116]
实施例四
[0117]
参照图1，一种基于人工神经网络技术的有限元数值模拟后验误差估计方法，包括如下步骤：
[0118]
步骤1、在静电场的分析区域ω计算有限元数值解；
[0119]
步骤1.1、确定静电场的分析区域ω并测量，然后测定分析区域的电荷密度、分析区域边界处的电势值；
[0120]
建立静电场泊松方程：
[0121]-δu＝f(x,y)
[0122]
u|
γ
＝0
[0123]
f(x,y)＝-δg(x,y)
[0124]
g(x,y)＝15xy(x-1)(y-1)exp(-40((x-0.5)2+(y-0.5)2))
[0125]
得到解析解u为：
[0126]
u＝15xy(x-1)(y-1)exp(-40((x-0.5)2+(y-0.5)2))
[0127]
步骤1.2、根据解析解u，应用有限元方法求解静电场泊松方程：
[0128]
将静电场泊松方程的分析区域ω作为计算区域ω进行剖分得到网格单元k的集合th，定义pk(k)表示在集合th中任意单元k上的次数不超过k的多项式函数空间，则在函数空间vh中存在有限元数值解uh，使得uh满足方程其中其中
[0129]
其中，u为未知电势函数，v为多项式函数，l2(ω)为在ω内所有平方可积的函数组成的函数空间，为sobolev空间，表示电荷密度，ε0＝8.854
×
10-12
f/m表示介电常数；
[0130]
图5是计算有限元数值解uh使用的网格，网格数为224；图14是解析解u的曲面图；图15是有限元数值解uh的曲面图；
[0131]
本实施例步骤2至4与实施例一相同；
[0132]
图16为本实施例神经网络训练20000步损失函数的收敛情况；图17为真实误差∈
*
的分布图，图18为本实施例所得的后验误差∈的分布图。
[0133]
实施例五
[0134]
本实施例应用实施例四相同泊松方程算例，计算有限元数值解uh所使用网格的网
格数为56，不重新训练神经网络，其余设置均与实施例四相同。
[0135]
图19为真实误差∈
*
的分布图，图20为本实施例所得的后验误差∈的分布图。
[0136]
实施例六
[0137]
本实施例应用实施例四相同泊松方程算例，计算有限元数值解uh所使用网格的网格数为896，不重新训练神经网络，其余设置均与实施例四相同。
[0138]
图21为真实误差∈
*
的分布图，图22为本实施例所得的后验误差∈的分布图。
[0139]
表2给出了实施例一至三的真实误差∈
*
与后验误差∈，结果表明本发明可以用于估计数值解的真实误差，可以看到本发明仍然能够准确地估计真实误差分布。
[0140]
表2
[0141]
实施例网格数真实误差后验误差是否训练网络四2240.80850.8092是五560.51010.5125否六8960.26090.2659否
[0142]
以上实施例仅用以说明本发明的技术方案，而非对其限制，对于本领域的普通专业技术人员来说，可以对前述各实施例所记载的具体技术方案进行修改，或者对其中部分技术特征进行等同替换，而这些修改或者替换，并不使相应技术方案的本质脱离本发明所保护技术方案的范围。