一种基于P-I模型的气动软体机械臂迟滞建模方法

一种基于p-i模型的气动软体机械臂迟滞建模方法
技术领域
1.本发明属于气动软体机械臂迟滞建模技术领域，具体涉及一种基于p-i模型的气动软体机械臂迟滞建模方法。


背景技术：

2.软体机器人是机器人领域研究的热点方向，相对于传统的刚性机器人，软体机器人具有安全性，在人机交互或者与受到冲击等的情况下，不会对人或物产生损伤；独有的柔顺性，使得软体机器人具有广阔的应用前景，在医疗康复、空间探索、农业生产等方面有较高的实际应用价值。
3.由硅胶等软质材料浇筑的软体机器人存在迟滞性突出的缺点，迟滞非线性现象会影响软体机器人的运动性能，为进一步的模型控制带来困难。迟滞现象多产生于非线性系统中，而软体机器人由软质材料构成，是典型的非线性系统，主要表现为系统的输出不仅与当下的输入值有关，与历史状态也有关系。迟滞现象对软体机器人的精确控制带来很大困难，基于以上软体机械臂模型，迟滞的产生主要由以下原因。
4.(1)设计的软体机械臂主要由硅胶等软质材料构成，软质材料相对于刚性材料非线性现象特征突出，难以控制，因此材料特性是软体机械臂产生迟滞的主要原因。(2)设计的软体机械臂耦合有堵塞变刚度结果，颗粒间摩擦与空隙，刚度的变化等容易产生迟滞。(3)在制备软体机械臂时，使用的硅胶溶液中存在微小气泡。
5.常见的迟滞模型有preisach模型、prandtl-ishlinskii(p-i)模型以及maxwell模型、bouc-wen模型等，对于preisach模型，可能会出现误差累积现象，maxwell模型相对来说比较复杂。


技术实现要素：

6.解决的技术问题：本发明公开了一种基于p-i模型的气动软体机械臂迟滞建模方法，在基本p-i模型的基础上，引申出一种mpi迟滞模型，并利用p-i模型以及mpi模型的算子在状态改变点处的性质得到p-i模型以及mpi模型的权值计算矩阵，该参数矩阵对于归一化后的迟滞模型具有通用性，通过该矩阵可方便得出模型参数，为软体机械臂的实时建模等情况提供一个解决方法。
7.技术方案：
8.一种基于p-i模型的气动软体机械臂迟滞建模方法，所述气动软体机械臂计包括软体机械臂的气动驱动结构以及变刚度结构；所述气动软体机械臂迟滞建模方法包括以下步骤：
9.s1，将不同阈值下的play算子加权叠加构成p-i模型：
[0010][0011]
其中，n表示算子的个数，wi表示第i个算子的权值，ri表示第i个算子的阈值，y(k)
为k时刻建立模型的输出；yi[u(k)，ri]为play算子在阈值为ri时，第k时刻的输出；u(k)为在k时刻算子的输入；
[0012]
s2，由一个play算子、n个上升算子、n个下降算子构成气动软体机械臂中的非对称迟滞模型：
[0013][0014]
其中，w0，w
ai
，w
di
为权重参数；u(k)为k时刻的输入；ri为在k时刻时，不同算子的阈值；y(k)为k时刻模型的输出；ai[u(k)，ri]表示阈值为ri的k时刻的上升算子；di[u(k)，ri]表示阈值为ri的k时刻的下降算子；
[0015]
s3，对气动软体机械臂中的非对称迟滞模型中的参数进行辨识；具体地，对输入值以及响应值做归一化处理，归一化后的每一个模型输出点y(k)是由n+1个算子加权叠加构成，当阈值r和输入u(k)确定，n+1个算子的值也确定，通过解方程组求解得到p-i模型参数的未知权值参数；根据上升算子和下降算子在状态改变点处的性质，结合测量得到归一化后的输出，求得气动软体机械臂中的非对称迟滞模型的未知权值参数。
[0016]
进一步地，步骤s1中，play算子的表达式为：
[0017][0018]
其中，r为play算子的阈值，u(k)为k时刻算子的输入。
[0019]
进一步地，步骤s2中，所述上升算子的表达式为：
[0020]ai
[u(k)，ri]＝(u(k)+r-yi[u(k)，ri])
·
yi[u(k)，ri]；
[0021]
所述下降算子的表达式为：
[0022]di
[u(k)，ri]＝(yi[u(k)，ri]-u(k)+r)
·
yi[u(k)，ri]
[0023]
上升算子和下降算子与阈值r以及k时刻的输入有关。
[0024]
进一步地，步骤s3中，采用下述公式对输入值以及响应值做归一化处理：
[0025]
un(k)＝(u(k)-um)/(u
m-um)
[0026]
xn(k)＝(x(k)-xm)/(x
m-xm)
[0027]
式中，对于无耦合变刚度结构的气动软体机械臂，u(k)为第k个输入的气压数据，um为输入气压的最小值，um为输入气压的最大值，un(k)为第k个输入气压归一化后的值；x(k)为第k个输出的位移值，xm为输出位移的最小值，xm为输出位移的最大值；
[0028]
对于耦合变刚度结构气动软体机械臂，u(k)为第k个末端位移值，um为末端位移的最小值，um为末端位移的最大值，un(k)为第k个末端位移归一化后的值；x(k)为第k个末端位移对应的末端接触力的值，xm为末端接触力的最小值，xm为末端接触力的最小值。
[0029]
进一步地，步骤s3中，通过解方程组求解得到p-i模型参数的未知权值参数的过程包括以下步骤：
[0030]
定义状态改变点集合，状态改变点v集合为横坐标上为2ri和1-2ri点的集合；对于一个由n+1个play算子叠加构成的迟滞模型，有2n个状态改变点，在对迟滞数据进行归一化处理后，上升阶段和下降阶段都包括状态改变点(0，0)和(1，1)，上升阶段和下降阶段各包
括n+1个状态改变点；
[0031]
在上升阶段，假设有一状态改变点为v(k)，则存在某一阈值为ri的play算子满足下述公式：ri＝v(k)/2；以ri的值为分界点将p-i模型的n+1个算子分为两类，一类为阈值rm小于等于ri，一类为阈值rm大于ri；当第一类算子的阈值rm小于等于ri时，在状态改变点v(k)处的输出为v(k)-rm；当第二类算子阈值rm大于ri时，在状态改变点处的输出为rm；
[0032]
在下降阶段，同样以ri的值为分界点将p-i模型的n+1个算子分为两类，一类为阈值rm小于等于ri，一类为阈值rm大于ri；当第一类算子的阈值rm小于等于ri时，在状态改变点v(k)处的输出为v(k)+rm；当第二类算子阈值rm大于ri时，在状态改变点处的输出为1-rm；
[0033]
根据状态改变点的性质，再结合步骤s1的p-i模型，得到在状态改变点v(k)处的模型的输出为：
[0034][0035]
将得到的方程合并展开，得到权值系数矩阵的求解方程：
[0036][0037]
式中，x0(k)，x1(k)，...，xn(k)为归一化后的输出，对于归一化后的软体机械臂末端位移值，为已知量；rm为小于等于ri的阈值，v(k)为第k个状态改变点，rm也为已知量；对于u(k)-rm，u(k)为归一化的输入值；对于归一化的输入气压值，u(k)-rm也为已知量。
[0038]
进一步地，步骤s3中，求得气动软体机械臂中的非对称迟滞模型的未知权值参数的过程包括以下步骤：
[0039]
对于任意状态改变点v(k)，均存在一个阈值为ri的算子满足公式ri＝v(k)/2；以求得的阈值ri为分界点，将算子分为两类，第一类算子的阈值0≤rm＜ri，第二类算子阈值为rm≥ri；
[0040]
在上升阶段，第一类算子中，当rm＝0时，对应的为阈值r为0的play算子，阈值r为0的play算子在状态改变点v(k)处满足公式α＝y0[v(k)，r0]＝v(k)；当阈值r＝0时，play算子退化为一条重合的直线，算子的输出等于算子的输入v(k)：α＝y0[v(k)，r0]＝v(k)；
[0041]
对于第一类算子，当0＜rm＜ri时，阈值为rm的上升算子在状态改变点v(k)处的输出为：
[0042]
β
′
＝(v(k)+r
m-ym[v(k)，rm])
·
ym[v(k)，rm]k＝1，2，
…
，i-1
[0043]
其中ym[v(k)，rm]为阈值为rm的play算子在状态改变点v(k)处的输出，为v(k)-rm；转换得到：β
′
＝2rm·
(v(k)-rm)，k＝1，2，
…
，i-1；
[0044]
对于第一类算子，当0＜rm＜ri时，阈值为rm的下降算子在状态改变点v(k)处的输出为：β
″
＝(ym[v(k)，rm]-v(k)+rm)
·
ym[v(k)，rm]；其中，ym[v(k)，rm]同样为阈值为rm的play算子在状态改变点v(k)处的输出，为v(k)-rm；转换得到：β
″
＝0，k＝1，2，
…
，i-1；
[0045]
对于第二类算子，当算子阈值rm≥ri时，阈值为rm的上升算子在状态改变点v(k)、处的输出为：γ
′
＝(v(k)+r
m-ym[v(k)，rm])
·
ym[v(k)，rm]k＝i，i+1，
…
，n，其中ym[v(k)，rm]为阈值为rm的play算子在状态改变点v(k)处的输出，rm≥ri，play算子输出为rm，转换得到：γ
′
＝v(k)
·rm k＝i，i+1，
…
，n；
[0046]
对于第二类算子，当算子阈值rm≥ri时，阈值为rm的上升算子在状态改变点v(k)处的输出为：γ
″
＝(ym[v(k)，rm]-v(k)+rm)
·
ym[v(k)，rm]，其中ym[v(k)，rm]为阈值为rm的play算子在状态改变点v(k)处的输出，rm≥ri，play算子输出为rm，转换得到：γ
″
＝(2
·rm-v(k))
·rm k＝i，i+1，
…
，n；
[0047]
在下降阶段，在第一类算子中，当rm＝0时，对应的为阈值r为0的play算子，阈值r为0的play算子在状态改变点v(k)处满足：α＝y0[v(k)，r0]＝v(k)；
[0048]
对于第一类算子，当0《rm＜ri时，阈值为rm的上升算子在状态改变点v(k)处的输出为：β
′
＝(v(k)+r
m-ym[v(k)，rm])
·
ym[v(k)，rm]，其中ym[v(k)，rm]为阈值为rm的play算子在下降阶段的状态改变点v(k)处的输出，为v(k)+rm，转换得到：β
′
＝0，k＝1，2，
…
，i-1；
[0049]
对于第一类算子，当0＜rm＜ri时，阈值为rm的下降算子在状态改变点v(k)处的输出为：β
″
＝(ym[v(k)，rm]-v(k)+rm)
·
ym[v(k)，rm]，其中，ym[v(k)，rm]同样为阈值为rm的play算子在状态改变点v(k)处的输出，为v(k)+rm，转换得到：β
″
＝2
·rm
·
(v(k)+rm)，k＝1，2，
…
，i-1
[0050]
对于第二类算子，当算子阈值rm≥ri时，阈值为rm的上升算子在状态改变点v(k)处的输出为：γ
′
＝(v(k)+r
m-ym[v(k)，rm])
·
ym[v(k)，rm]k＝i，i+1，
…
，n，其中ym[v(k)，rm]为阈值为rm的play算子在状态改变点v(k)处的输出，rm≥ri，play算子输出为1-rm，转换得到：γ
′
＝(v(k)-1+2rm)
·
(1-rm)k＝i，i+1，
…
，n；
[0051]
对于第二类算子，当算子阈值rm≥ri时，阈值为rm的上升算子在状态改变点v(k)处的输出为：γ
″
＝(ym[v(k)，rm]-v(k)+rm)
·
ym[v(k)，rm]，其中ym[v(k)，rm]为阈值为rm的play算子在状态改变点v(k)处的输出，rm≥ri，play算子输出为1-rm，转换得到：γ
″
＝(1-v(k))
·
(1-rm)k＝i，i+1，
…
，n；
[0052]
根据上升算子和下降算子在状态改变点处的性质，得到非对称迟滞模型在上升段的状态改变点处v(k)的输出为：
[0053][0054]
在下降段，得到非对称迟滞模型在下降段的状态改变点处v(k)的输出为：
[0055][0056]
令w
an
＝w
dn
，得到下述方程组，求解2n个未知权重参数w0，wn，wa，wd：
[0057][0058]
进一步地，所述气动软体机械臂迟滞建模方法包括以下步骤：
[0059]
对p-i模型求逆，其中，相应的逆模型的参数计算公式为：
[0060][0061][0062][0063]
进一步地，所述p-i模型的模型验证过程包括：
[0064]
归一化迟滞数据b，选取上升段的11个数据点；
[0065]
根据下述公式计算得到权值参数：w＝a-1
·
b；
[0066]
对得到的权值参数与play算子进行加权叠加，得到每个迟滞数据点对应的建模点y(k)：
[0067]
计算迟滞数据b与建模数据y(k)之间的差值，作为建模误差。
[0068]
进一步地，所述气动软体机械臂中的非对称迟滞模型的模型验证过程包括：
[0069]
归一化迟滞数据b，以固定间隔选取20个数据点；
[0070]
根据下述公式计算得到权值参数：w＝a-1
·
b；
[0071]
对得到的权值参数与play算子进行加权叠加，得到每个迟滞数据点对应的建模点y(k)：
[0072]
计算迟滞数据b与建模数据y(k)之间的差值，作为建模误差。
[0073]
有益效果：
[0074]
第一，本发明的基于p-i模型的气动软体机械臂迟滞建模方法，利用p-i模型算子的特性，得到p-i模型以及mpi模型参数矩阵，该参数矩阵对于归一化后的迟滞模型具有通用性，可方便得出模型参数，为软体机械臂的实时建模等情况提供一个解决方法。
[0075]
第二，本发明的基于p-i模型的气动软体机械臂迟滞建模方法，给出参数计算矩阵具有唯一解证明，以及迟滞模型的具体验证方法及步骤，使用p-i模型、mpi模型对测量得到的迟滞曲线进行拟合，求得迟滞参数，通过仿真分析验证模型的正确性。
附图说明
[0076]
图1为软体机械臂整体结构示意图，(a)为俯视图，(b)为正视图；
[0077]
图2为阈值为0.1和0.3的play算子示意图；
[0078]
图3为p-i模型加权叠加结构示意图；
[0079]
图4为阈值r＝0.2和0.3时的上升算子示意图；
[0080]
图5为阈值r＝0.2和0.3时的下降算子示意图；
[0081]
图6为mpi模型加权叠加结构示意图；
[0082]
图7为p-i模型上升段权值参数计算流程图；
[0083]
图8为阈值r＝0的play算子示意图；
[0084]
图9为mpi模型参数计算流程图；
[0085]
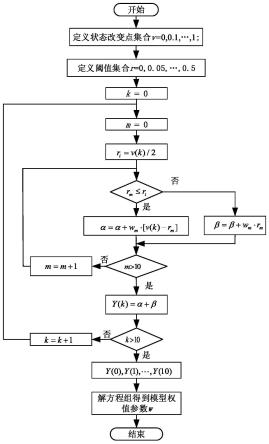
图10是参数计算流程图；
[0086]
图11为p-i迟滞模型验证流程图；
[0087]
图12为mpi迟滞模型验证流程图。
具体实施方式
[0088]
下面的实施例可使本专业技术人员更全面地理解本发明，但不以任何方式限制本发明。
[0089]
软体机械臂的结构设计包括软体机械臂的气动驱动结构以及变刚度结构，本小节针对软体机械臂的整体结构进行说明。
[0090]
软体驱动器的整体结构如图1所示，如图1中的(a)为整个软体机械臂的俯视图，由俯视图可以看出，整个机械臂由三个气腔、耦合变刚度结构的空腔构成，其中堵塞变刚度结构空腔位于软体机械臂中心位置，为制作的变刚度结构预留装配位置，三个空腔位于形变层内，呈120
°
分布。如图1中的(b)所示为软体机械臂正视图，在机械臂的末端分布有三个充气管道和一个真空管道，当充气时，空腔压强变化，从而发生运动；有一个抽气管道，当气动软体机械臂需要改变刚度时，通过抽气改变堵塞结构的真空度，从而改变刚度。
[0091]
本实施例公开了一种基于p-i模型的气动软体机械臂迟滞建模方法，所述气动软体机械臂计包括软体机械臂的气动驱动结构以及变刚度结构；所述气动软体机械臂迟滞建模方法包括以下步骤：
[0092]
s1，将不同阈值下的play算子加权叠加构成p-i模型：
[0093]
[0094]
其中，n表示算子的个数，wi表示第i个算子的权值，ri表示第i个算子的阈值，y(k)为k时刻建立模型的输出；yi[u(k)，ri]为play算子在阈值为ri时，第k时刻的输出；u(k)为在k时刻算子的输入；
[0095]
s2，由一个play算子、n个上升算子、n个下降算子构成气动软体机械臂中的非对称迟滞模型：
[0096][0097]
其中，w0，w
ai
，w
di
为权重参数；u(k)为k时刻的输入；ri为在k时刻时，不同算子的阈值；y(k)为k时刻模型的输出；ai[u(k)，ri]表示阈值为ri的k时刻的上升算子；di[u(k)，ri]表示阈值为ri的k时刻的下降算子；
[0098]
s3，对气动软体机械臂中的非对称迟滞模型中的参数进行辨识；具体地，对输入值以及响应值做归一化处理，归一化后的每一个模型输出点y(k)是由n+1个算子加权叠加构成，当阈值r和输入u(k)确定，n+1个算子的值也确定，通过解方程组求解得到p-i模型参数的未知权值参数；根据上升算子和下降算子在状态改变点处的性质，结合测量得到归一化后的输出，求得气动软体机械臂中的非对称迟滞模型的未知权值参数。
[0099]
(一)p-i模型建立
[0100]
p-i模型是由一系列p-i算子加权相加而成，p-i算子分为play算子和stop算子，两者是互补的关系，本文建立的p-i模型是基于play算子，play算子的表达式如公式(3.1)所示。
[0101][0102]
其中r为当前play算子的阈值，u(k)为k时刻算子的输入。如图2为play算子阈值r＝0.1与0.3时的play算子。由公式3.1和图2可以看出，算子的输出与阈值r和k时刻的输入有关，因此使用yi[u(k)，ri]表示当阈值为ri，输入为u(k)时，第i个算子的输出。
[0103]
p-i模型是不同阈值下的play算子加权叠加构成，每个算子的权值不同，其结构如图3所示，其中每个算子对应的权值不同，且算子的阈值r也不相同，加权相加后在k时刻表达式如公式(3.2)所示：
[0104][0105]
公式(3.2)中，n表示算子的个数，wi表示第i个算子的权值，ri表示第i个算子的阈值。y(k)即为k时刻建立模型的输出。为了表示方便，可以将公式(3.2)写为如公式(3.3)所示的向量模式。
[0106]
y(k)＝w
t
·
y，[u(k)，ri]
ꢀꢀꢀꢀꢀꢀꢀꢀ
(3.3)
[0107]
公式中w为权值向量，w＝(w0，w1，
…
，wn)，y[u(k)，ri]为k时刻算子的状态向量。
[0108]
(二)mpi模型建立
[0109]
由图3可以看出play算子是对称的，因此play算子的加权叠加也只能描述对称的迟滞模型，然而软体机械臂的迟滞现象总是非对称的，因此在play算子的基础上使用两种
改进的算子，用来描述软体机械臂的非对称的迟滞现象。非对称的迟滞为软体机械臂的迟滞回线是非对称的，即上升曲线不能通过旋转得到下降曲线。
[0110]
上升算子的定义如公式(3.4)所示，其中ai[u(k)，ri]为上升算子第k时刻的输出，yi[u(k)，ri]为play算子在阈值为ri时，第k时刻的输出，u(k)为在k时刻算子的输入：
[0111]ai
[u(k)，ri]＝(u(k)+r-yi[u(k)，ri])
·
yi[u(k)，ri]
ꢀꢀꢀꢀ
(3.4)。
[0112]
下降算子的定义如公式(3.5)所示，公式中变量的含义与公式(3.4)相同：
[0113]di
[u(k)，ri]＝(yi[u(k)，ri]-u(k)+r)
·
yi[u(k)，ri]
ꢀꢀꢀ
(3.5)。
[0114]
上升算子和下降算子与阈值r，以及k时刻的输入有关，为了方便，使用ai[u(k)，ri]表示阈值为ri，k时刻的上升算子，使用di[u(k)，ri]表示阈值为ri，k时刻的下降算子。
[0115]
如图4所示为阈值为0.2和0.3的上升算子，图5所示为阈值为0.2和0.3的下降算子，从图4和图5中可以看出，上升算子和下降算子均为非对称结构，可以用来描述非对称迟滞现象。
[0116]
mpi模型仍然属于p-i模型的范畴，mpi模型与p-i模型类似，也是多个算子的加权叠加而成，加权叠加后如公式(3.6)所示，其结构如图6所示，在某一刻模型的输出由一个play算子、n个上升算子、n个下降算子构成，相对而言p-i模型仅仅由n个play算子加权叠加，因而mpi模型能够更好的表征气动软体机械臂中的非对称迟滞模型：
[0117][0118]
其中，w0，w
ai
，w
di
为权重参数，u(k)为k时刻的输入，ri为在k时刻时，不同算子的阈值。y(k)为k时刻模型的输出。
[0119]
在上述模型中，w0，w
ai
，w
di
为算子权重，是未知量，其中：
[0120]wai
＝[w
a1
，w
a2
，
…
，w
ai
，
…
，w
an
]
t
ꢀꢀꢀꢀ
(3.7)
[0121]
同样的，
[0122]wdi
＝[w
d1
，w
d2
，
…
，w
di
，
…
，w
dn
]
t
ꢀꢀꢀꢀ
(3.8)
[0123]
不同的权重组合可以得到不同的迟滞模型，因此对w0，w
ai
，w
di
求解完成后，就可以建立完整的软体机械臂迟滞模型。
[0124]
(三)p-i模型以及mpi模型参数辨识
[0125]
p-i模型是一种基于现象的迟滞模型，仅根据测量得到的数据就能建立模型，而不用考虑材料的特性。在进行参数辨识之前，首先对输入值以及响应值做归一化处理，本文基于软体机械臂中存在的气压与位移迟滞现象、位移与末端接触力的迟滞现象进行建模分析。对于气压-位移迟滞现象输入为气压，三个气腔中气压相同，测量得到的物理量为软体机械臂的伸长量；对于位移-气动软体机械臂末端接触力，通过改变堵塞结构内的真空度(设定为0kpa和40kpa)，通过改变软体机械臂的末端位移，测量得到末端接触力。归一化公式如公式(3.9)、(3.10)所示。
[0126]
un(k)＝(u(k)-um)/(u
m-um)
ꢀꢀꢀꢀꢀꢀꢀꢀ
(3.9)
[0127]
xn(k)＝(x(k)-xm)/(x
m-xm)
ꢀꢀꢀꢀꢀꢀꢀ
(3.10)
[0128]
公式中(3.9)中，对于无耦合变刚度结构的气动软体机械臂，u(k)为第k个输入的气压数据，um为输入气压的最小值，um为输入气压的最大值，un(k)即为第k个输入气压归一化后的值。公式(3.10)中，x(k)为第k个输出的位移值，xm为输出位移的最小值，xm为输出位
移的最大值。对于耦合变刚度结构气动软体机械臂，公式中(3.9)中，u(k)为第k个末端位移值，um为末端位移的最小值，um为末端位移的最大值，un(k)为第k个末端位移归一化后的值，公式中(3.10)中，x(k)为第k个末端位移对应的末端接触力的值，xm为末端接触力的最小值，xm为末端接触力的最小值。
[0129]
(3.1)p-i模型参数辨识
[0130]
对play算子而言，其输出仅与阈值r和输入u(k)有关，当通过公式(3.9)将输入值u(k)归一化，并取算子的阈值r为0，0.05，0.1，...，0.5后，当给定任意阈值r和归一化后的输入u(k)都可以唯一确定play算子的输出。根据这一结论，结合公式(3.2)，对于归一化后的每一个模型输出点y(k)是由n+1个算子加权叠加构成，当阈值r和输入u(k)确定，n+1个算子的值可以确定，因此公式(3.2)中剩余权值参数w
i i＝0，1，
…
，n为未知量，当取n+1个归一化后的输出值作为y(k)，通过解方程组即可求解得到p-i模型参数w[56]，其模型参数计算流程图如图7所示：在图7中u(k)，v(k)分别表示归一化后的第k+1个输入点以及第k+1个状态改变点，k＝0，1，2，...，10。
[0131]
在图7中，状态改变点v的定义为横坐标上为2ri和1-2ri点的集合，其中r为0，0.05，0.1，
…
，0.5，因此可以得到v＝0，0.1，
…
，1，在状态改变点处有以下性质：
[0132]
(1)在上升阶段，对于一个阈值为ri的play算子，由公式3.1可知，当横坐标小于2ri时，纵坐标保持不变为ri，当横坐标大于2ri时，纵坐标的值为u(k)-ri，对于横坐标为2ri的点，定义为上升阶段的状态改变点；
[0133]
(2)在下降阶段，横坐标大于1-2ri时，纵坐标保持为1-ri，横坐标小于1-2ri时，纵坐标为u(k)+ri；对于横坐标为1-2ri的点，定义为下降阶段的状态改变点；
[0134]
(3)对于一个由n+1个play算子叠加构成的迟滞模型，则有2n个状态改变点，在对迟滞数据进行归一化处理后，上升阶段和下降阶段都包括状态改变点(0，0)和(1，1)，因此上升阶段和下降阶段都包括n+1个状态改变点。在流程图7中是以上升阶段归一化的数据进行参数计算，因此只涉及上升阶段的状态改变点，因此集合v＝0，0.1，...，1；
[0135]
(4)在上升阶段，假设有一状态改变点为v(k)，由性质1可知则必然存在某一阈值为ri的play算子，满足公式(3.11)。
[0136]ri
＝v(k)/2
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3.11)
[0137]
以ri的值为分界点将p-i模型的n+1个算子分为两类，一类为阈值rm小于等于ri，一类为阈值rm大于ri。当第一类算子的阈值rm小于等于ri时，在状态改变点v(k)处的输出为v(k)-rm；当第二类算子阈值rm大于ri时，在状态改变点处的输出为rm。
[0138]
(5)在下降阶段，同样以ri的值为分界点将p-i模型的n+1个算子分为两类，一类为阈值rm小于等于ri，一类为阈值rm大于ri。当第一类算子的阈值rm小于等于ri时，在状态改变点v(k)处的输出为v(k)+rm；当第二类算子阈值rm大于ri时，在状态改变点处的输出为1-rm。
[0139]
根据状态改变点的性质，再结合p-i模型的定义公式(3.2)，结合流程图7可以得到在状态改变点v(k)处的模型的输出为公式(3.12)所示：
[0140][0141]
在p-i模型的上升阶段中，共有11个状态改变点(n＝10)，在每个状态改变点处都能得到如公式(3.12)所示的等式，将得到的方程合并展开，如公式(3.13)所示，
[0142][0143]
其中x0(k)，x1(k)，
…
，xn(k)为归一化后的输出，对于本文为归一化后的软体机械臂末端位移值，为已知量；由流程图7可知，rm为小于等于ri的阈值，且ri可根据公式(3.11)求得，公式(3.11)中v(k)为第k个状态改变点，因此rm也为已知量；对于u(k)-rm，k＝0，1，...，10，u(k)为归一化的输入值，对于本文为归一化的输入气压值，因此u(k)-rm也为已知量。因此在公式(3.13)中，仅有权值w为未知量，并且权值w的系数只与阈值r以及归一化后的输入有关，与输出无关，因此得到的权值系数矩阵为固定矩阵。经过计算，对于由11个play算子加权叠加构成的p-i模型，且取阈值r＝0，0.05，0.1，...，0.5时，其权值计算矩阵如公式(3.14)所示：
[0144][0145]
(3.2)mpi模型参数辨识
[0146]
mpi模型参数计算流程图如图9所示，与p-i模型参数计算流程图相似，集合v＝0，0.1，...，1，0.9，...，0.1表示状态改变点的集合，在流程图中v(k)表示第k+1个状态改变点，例如v(0)＝0，v(1)＝0.1，...，v(10)＝1：集合r＝0，0.05，0.1，
…
，0.5表示算子阈值，在流程图中，rm表示第m+1个阈值，例如r0＝0，r1＝0.05，...，r
10
＝0.5等。
[0147]
上升算子和下降算子在状态改变点时具有以下性质：
[0148]
(1)对于任意状态改变点v(k)，均存在一个阈值为ri的算子(play算子、上升或者下降算子)满足公式(3.11)。以公式(3.11)求得的阈值ri为分界点，将算子分为两类，第一类算子的阈值0≤rm＜ri，第二类算子阈值为rm≥ri。
[0149]
(2)在上升阶段，第一类算子中，当rm＝0时，由公式(3.6)可知，对应的为阈值r为0的play算子。阈值r为0的play算子在状态改变点v(k)处满足公式(3.15)，即当算子输入为v(k)，算子输出为v(k)。当阈值r＝0时，play算子退化为一条重合的直线，如图8所示，算子的输出等于算子的输入v(k)。
[0150]
α＝y0[v(k)，r0]＝v(k)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3.15)
[0151]
对于第一类算子，当0＜rm＜ri时，根据上升算子的定义公式(3.4)可知，阈值为rm的上升算子在状态改变点v(k)，k＝1，2，
…
，i-1处的输出为公式(3.16)所示：
[0152]
β
′
＝(v(k)+r
m-ym[v(k)，rm])
·
ym[v(k)，rm] k＝1，2，
…
，i-1
ꢀꢀꢀ
(3.16)
[0153]
其中ym[v(k)，rm]为阈值为rm的play算子在状态改变点v(k)处的输出，为v(k)-rm。因此可将公式(3.16)转换为公式(3.17)：
[0154]
β
′
＝2rm·
(v(k)-rm)，k＝1，2，
…
，i-1
ꢀꢀꢀ
(3.17)。
[0155]
对于第一类算子，当0＜rm＜ri时，根据下降算子的定义公式(3.5)，阈值为rm的下降算子在状态改变点v(k)，k＝1，2，...，i-1处的输出如公式(3.18)所示：
[0156]
β
″
＝(ym[v(k)，rm]-v(k)+rm)
·
ym[v(k)，rm]
ꢀꢀꢀꢀꢀꢀ
(3.18)
[0157]
其中，ym[v(k)，rm]同样为阈值为rm的play算子在状态改变点v(k)处的输出，为v(k)-rm。可将公式(3.18)转换为公式(3.19)所示。
[0158]
β
″
＝0，k＝1，2，
…
，i-1
ꢀꢀꢀꢀꢀꢀꢀꢀ
(3.19)
[0159]
对于第二类算子，即算子阈值rm≥ri时，同样根据上升算子的定义公式(3.4)可知阈值为rm的上升算子在状态改变点v(k)，k＝1，2，
…
，i-1处的输出为公式(3.20)所示：
[0160]
γ
′
＝(v(k)+r
m-ym[v(k)，rm])
·
ym[v(k)，rm] k＝i，i+1，
…
，n
ꢀꢀꢀ
(3.20)
[0161]
其中ym[v(k)，rm]为阈值为rm的play算子在状态改变点v(k)处的输出，此时rm≥ri，因此play算子输出为rm，因此可将公式(3.20)转换为公式(3.21)：
[0162]
γ
′
＝v(k)
·rm k＝i，i+1，
…
，n
ꢀꢀꢀ
(3.21)。
[0163]
同样对于第二类算子，当算子阈值rm≥ri时，同样根据下降算子的定义公式(3.5)可知阈值为rm的上升算子在状态改变点v(k)，k＝1，2，
…
，i-1处的输出为公式(3.22)所示：
[0164]
γ
″
＝(ym[v(k)，rm]-v(k)+rm)
·
ym[v(k)，rm]
ꢀꢀꢀ
(3.22)
[0165]
其中ym[v(k)，rm]为阈值为rm的play算子在状态改变点v(k)处的输出，此时rm≥ri，因此play算子输出为rm，因此可将公式(3.22)转换为公式(3.23)：
[0166]
γ
″
＝(2
·rm-v(k))
·rm k＝i，i+1，
…
，n
ꢀꢀꢀ
(3.23)。
[0167]
(3)同理，在下降阶段，在第一类算子中，当rm＝0时，由公式(3.6)可知，对应的为阈值r为0的play算子。阈值r为0的play算子在状态改变点v(k)处满足公式(3.24)，即当算子输入为v(k)，算子输出为v(k)。
[0168]
α＝y0[v(k)，r0]＝v(k)
ꢀꢀꢀꢀꢀꢀꢀ
(3.24)
[0169]
对于第一类算子，当0＜rm＜ri时，根据上升算子的定义公式(3.4)可知，阈值为rm的上升算子在状态改变点v(k)，k＝1，2，...，i-1处的输出为公式(3.25)所示：
[0170]
β
′
＝(v(k)+r
m-ym[v(k)，rm])
·
ym[v(k)，rm]
ꢀꢀꢀꢀꢀꢀ
(3.25)
[0171]
其中ym[v(k)，rm]为阈值为rm的play算子在下降阶段的状态改变点v(k)处的输出，为v(k)+rm。因此可将公式(3.25)转换为公式(3.26)：
[0172]
β
′
＝0，k＝1，2，
…
，i-1
ꢀꢀꢀꢀꢀꢀꢀꢀ
(3.26)
[0173]
对于第一类算子，当0＜rm＜ri时，根据下降算子的定义公式(3.5)，阈值为rm的下降算子在状态改变点v(k)，k＝1，2，...，i-1处的输出如公式(3.27)所示：
[0174]
β
″
＝(ym[v(k)，rm]-v(k)+rm)
·
ym[v(k)，rm]
ꢀꢀꢀꢀ
(3.27)
[0175]
其中，ym[v(k)，rm]同样为阈值为rm的play算子在状态改变点v(k)处的输出，为v(k)+rm。可将公式(3.27)转换为公式(3.28)所示：
[0176]
β
″
＝2
·rm
·
(v(k)+rm)，k＝1，2，
…
，i-1
ꢀꢀꢀꢀꢀ
(3.28)。
[0177]
对于第二类算子，即算子阈值rm≥ri时，同样根据上升算子的定义公式(3.4)可知阈值为rm的上升算子在状态改变点v(k)，k＝1，2，...，i-1处的输出为公式(3.29)所示。
[0178]
γ
′
＝(v(k)+r
m-ym[v(k)，rm])
·
ym[v(k)，rm] k＝i，i+1，
…
，n
[0179]
(3.29)
[0180]
其中ym[v(k)，rm]为阈值为rm的play算子在状态改变点v(k)处的输出，此时rm≥ri，因此play算子输出为1-rm，因此可将公式(3.29)转换为公式(3.30)：
[0181]
γ
′
＝(v(k)-1+2rm)
·
(1-rm) k＝i，i+1，
…
，n
ꢀꢀꢀꢀ
(3.30)。
[0182]
同样对于第二类算子，当算子阈值rm≥ri时，同样根据下降算子的定义公式(3.5)可知阈值为rm的上升算子在状态改变点v(k)，k＝1，2，
…
，i-1处的输出为公式(3.31)所示：
[0183]
γ
″
＝(ym[v(k)，rm]-v(k)+rm)
·
ym[v(k)，rm]
ꢀꢀꢀ
(3.31)
[0184]
其中ym[v(k)，rm]为阈值为rm的play算子在状态改变点v(k)处的输出，此时rm≥ri，因此play算子输出为1-rm，因此可将公式(3.31)转换为公式(3.32)：
[0185]
γ
″
＝(1-v(k))
·
(1-rm) k＝i，i+1，
…
，n
ꢀꢀꢀꢀ
(3.32)。
[0186]
结合以上三条性质和参数计算步骤流程图9，可以得到mpi模型参数计算仍然是先得到若干个含有参数的方程，然后展开合并，结合测量得到归一化后的输出即可求得模型权值参数。根据上升算子和下降算子在状态改变点处的性质，将公式(3.15)、(3.17)、(3.19)、(3.21)、(3.23)代入公式(3.6)可得mpi模型在上升段的状态改变点处v(k)的输出为公式(3.33)所示：
[0187][0188]
同理，在下降段，将公式(3.24)，(3.26)，(3.28)，(3.30)，(3.32)代入公式(3.6)可得mpi模型在下降段的状态改变点处v(k)的输出为公式(3.34)所示：
[0189][0190]
将公式(3.33)、(3.34)展开后合并，为了简便计算，令w
an
＝w
dn
，可得方程组如公式(3.35)所示，方程组中包含2n个方程，可求解2n个未知权重参数w0，wn，wa，wd：
[0191][0192]
公式(3.35)与公式(3.13)相似，有2n个未知权重参数w0，wn，wa，wd，当n取10时，有20个未知参数，为w0，w
10
，w
a1
，
…wa9
，w
d1
，
…wd9
。在公式(3.35)中，有2n个参数和2n个方程，因此可求得权重向量，可将公式化简为a
×
w＝b的形式，其中a为20*20的矩阵。对于这种方法，将经过归一化后的20个迟滞数据作为y(1)，...，y(2n)，即b的值；由于设定阈值r为固定值，并且输入值归一化到[0，1]中，因此矩阵a为固定矩阵，如公式(3.36)所示：
[0193][0194]
(3.36)。
[0195]
(四)p-i以及mpi逆迟滞模型
[0196]
如果想要进一步利用迟滞模型控制软体机械臂，还需要对迟滞模型求逆，得到迟滞逆模型。
[0197]
对于p-i模型，其逆模型仍为p-i模型，仅仅是权值以及阈值发生变化，其参数可由以下公式(3.37-3.39)求得：
[0198][0199][0200][0201]
由于mpi迟滞模型属于p-i模型的一种，都是不同的算子加权相加而成，因此他们的逆模型也是p-i模型的一种，是由多个算子加权相加，只是权值以及阈值发生改变，权值和阈值由公式(3.37-3.39)得出。
[0202]
(五)迟滞模型仿真步骤
[0203]
本部分进一步介绍如何利用参数辨识原理得到p-i模型以及mpi模型的参数；并根据迟滞模型的加权相加原理，将得到的参数代入算子中验证得到的权值参数的正确性。
[0204]
(5.1)p-i模型权值参数计算
[0205]
根据参数计算原理，参数w由公式(3.40)计算得到，在公式中，对于p-i模型而言，参数辨识矩阵a如公式(3.14)所示，b则为测量得到的上升段或者下降段的迟滞数据。
[0206]a·
w＝b
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3.40)
[0207]
参数计算流程如图10所示，其中利用公式(3.10)归一化数据，由于算子个数限制，因此需要在在归一化的数据中按照固定间隔取20个点构成离散状态下的迟滞环，对于p-i模型，可将上升段或者下降段的数据作为b，然后根据公式(3.40)的即可求出模型参数w。
[0208]
对于mpi模型参数计算矩阵如式(3.28)所示，其参数计算公式以及流程与p-i模型基本一致，仅在mpi模型中，将固定间隔取得的20个数据点作为b，再根据公式(3.40)求得参数w。
[0209]
根据p-i模型的加权相加原理，对得到的权值参数w结合相应的算子加权叠加从而验证参数以及模型的正确性。
[0210]
(5.2)权值参数唯一解证明
[0211]
对于线性方程组ax＝b有解的充分必要条件是r(a)＝r(a，b)，当a为公式(3.14)时，a为11*11矩阵，且由matlab计算可得，rank(a)＝11，且由于a为方阵，因此满足r(a)＝r(a，b)，又因为矩阵a秩等于行数，因此可得到方程组有唯一解。
[0212]
当参数计算矩阵a为公式(3.36)时，a为20*20矩阵，其rank(a)＝20，同样满足r(a)＝r(a，b)，又因为矩阵a秩等于行数，因此同样可以得到方程组有唯一解。
[0213]
(5.3)迟滞模型验证步骤
[0214]
由图3和图6可以看出，对于p-i模型是由不同权值算子加权叠加构成，基于得到的权值参数，结合play算子以及上升算子和下降算子验证模型的正确性。
[0215]
对于p-i模型的模型验证，具体流程图如图11所示，其中由于p-i模型是基于上升段或者下降段的数据进行建模，因此在归一化的数据b中选取其中一段数据点，在该流程图中选取上升段的数据点进行权值计算，对得到的权值参数与play算子进行加权叠加，得到每个迟滞数据点对应的建模点y(k)，其建模的误差可由迟滞数据b建模数据y(k)得到。对于mpi模型，其模型验证流程图如图12所示，由于mpi模型是由整个迟滞环数据计算权值，因此需要归一化整个迟滞环的数据，并且为了与mpi权值计算矩阵(3.36)相对应，需要以固定间
隔选取20个离散数据点作为b，用以计算权值w，w即为求得的权重参数(20x1)。
[0216]
对于本文mpi模型是由一个阈值为0的play算子，10个上升算子，10个下降算子加权叠加而成，由于wn＝w
an
＝w
dn
，因此仅需要20个方程计算得到参数。将权值w与对应的一个play算子和10个上升算子，10个下降算子加权叠加可得到对应的迟滞数据点处的建模值y(k)，对于建模误差值的计算，通过将相应的离散迟滞数据b减去建模数据y(k)即可得到每个离散点处的建模误差。
[0217]
本实施例在基本p-i模型的基础上，引申出一种mpi迟滞模型，并利用p-i模型以及mpi模型的算子在状态改变点处的性质得到p-i模型以及mpi模型的权值计算矩阵，该参数矩阵对于归一化后的迟滞模型具有通用性，矩阵如公式(3.14)和(3.36)所示，通过该矩阵可方便得出模型参数。最后详细描述了参数计算步骤、参数唯一解证明以及利用得到的权值参数验证模型的详细步骤。
[0218]
以上仅是本发明的优选实施方式，本发明的保护范围并不仅局限于上述实施例，凡属于本发明思路下的技术方案均属于本发明的保护范围。应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理前提下的若干改进和润饰，应视为本发明的保护范围。