基于增广拉格朗日方法的非线性极小化问题预处理方法

本发明涉及科学计算，特别是一种基于增广拉格朗日方法的非线性极小化问题预处理方法，主要涉及针对非线性约束条件的非线性极小化问题的预处理方法。

背景技术：

1、随着科学与工程研究的不断深入，计算过程越来越复杂，数值求解技术也得到了相应的发展，其中预处理技术能够根据原始偏微分方程组的性质和特征，将其由难以直接求逆的原始方程组变换为形式更简便、较易求逆的方程组，从而有效提高计算效率，因此引起了国际学术界和工程应用部门在复杂系统大规模计算方面的高度重视，并成为偏微分方程数值求解研究的一个热点。此前本发明第一发明人在数值模拟三维液晶系统的实际结果表明(j.xia,s.maclachlan,t.atherton,p.farrell.structural landscapes ofgeometrically frustrated smectics,physical review letters,2021.04)，从二维转向三维的数值求解复杂度急剧上升，而一味地通过细化网格来提高精度的方式则大大增加了计算量，计算耗时愈加令人难以接受，这也表明了需要设计一种快速求解算法以满足在大规模复杂系统中的数值应用需求。

2、在快速数值求解方面，采用有限元数值格式离散模型并使用牛顿迭代后，求解偏微分方程本质上最终变成了矩阵求逆的线性代数问题。一般可使用直接法(如lu分解，cholesky分解等)分解矩阵，但对于三维方程组，直接法的计算复杂度急剧上升，计算效率显著下降，因此，亟需设计与之配套的快速求解算法。针对这一现实问题，预处理技术从设计层面上要求变换后的方程组形式更为简便，易于计算，同时预处理器本身具有一定的特殊性质使其能够被快速分解，从而加快了求解效率。另一方面，为满足对复杂结构的细致刻画需求，一味地密分网格会增加计算负担，降低计算效率，因而可结合预处理器设计技术来保证较快的求解速度。

3、鉴于上述背景，从计算求解层面上，需要设计出一种方法结合预处理技术以提高算法对带有非线性约束条件的非线性极小化问题的数值计算效率，解决在高维问题上求解速度缓慢的问题。

技术实现思路

1、本发明的目的在于提供一种针对带有非线性约束条件的非线性极小化问题预处理方法，主要利用增广拉格朗日方法并基于有限元空间构造合理的光滑器。

2、实现本发明目的的技术解决方案为：基于增广拉格朗日方法的非线性极小化问题预处理方法，该方法针对带有非线性约束条件n·n＝1的极小化问题，具体表示为：

3、

4、并且n满足n·n＝1，           (1)

5、其中，ω＝{(x，y)：1≤x2+y2≤2.25}为一个二维圆环区域，x，y为直角坐标系标识，n为在区域ω上的未知向量函数，n∈h1(ω)表示n满足下列条件：

6、

7、其中，n·n表示向量n与其自身的乘积(即，若n＝[n1，n2，n3]t，则n·n＝(n1)2+(n2)2+(n3)2)，表示向量n的梯度(即，若n＝[n1，n2，n3]t，则其中x，y，z为三维直角坐标系的标识)，表示梯度与其自身的乘积(即，若n＝[n1，n2，n3]t，则具体分为以下步骤：

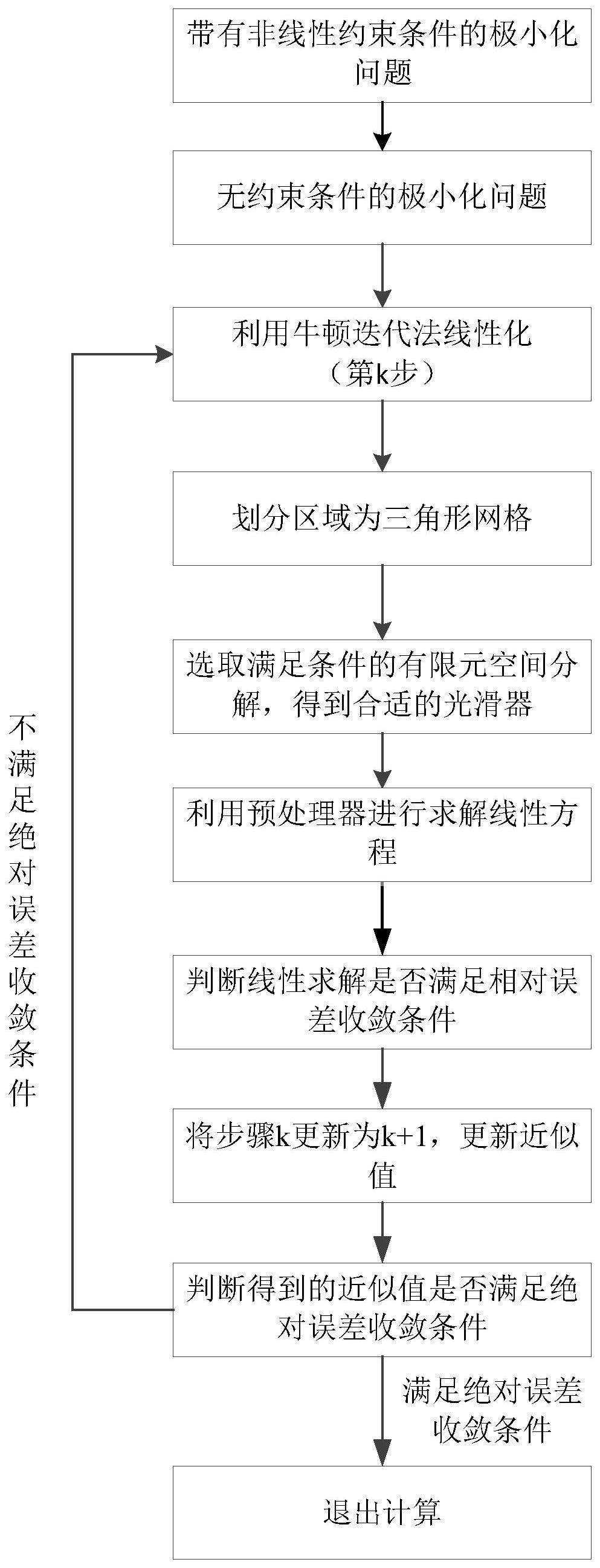
8、s1利用增广拉格朗日方法，引入拉格朗日乘子λ，从原始泛函j(n)得到目标泛函目标泛函在后续步骤中简写为此步骤主要完成将带有限制条件的原始泛函转换为不带有限制条件的目标泛函，有利于后续计算求解。

9、具体如下：

10、

11、其中，γ为增广系数，γ∈[103，106]，拉格朗日乘子λ是区域ω上的二次可积函数：λ∈l2(ω)，即满足∫ωλ2＜+∞。

12、在的表达式(2)中，泛函j(n)＝∫ωw(n)，w(n)表示能量密度函数，而且w(n)的一个具体表达式可以为

13、

14、其中，κ，v均为非负系数，取为κ＝0.1，v＝3.0，表示向量n的散度(即，若n＝[n1，n2，n3]t，表示向量n的旋度(即，若n＝[n1，n2，n3]t，则

15、因此，带有非线性约束条件n·n＝1的极小化问题(1)就转化为下列不带约束条件的极小化问题：

16、

17、进一步求得极小化问题(3)的欧拉-拉格朗日方程：

18、

19、下标表示分别对相应变量求偏导。

20、s2利用牛顿迭代法对欧拉-拉格朗日方程(4)进行线性化，以当前步骤k为基准，记nk，λk分别为n，λ在步骤k时的近似，定义从当前步骤k到下一步骤k+1的增量分别为δn＝nk+1-nk，δλ＝λk+1-λk，根据牛顿迭代法原理，当前步骤k上的线性方程为：

21、

22、其中，表示对分别关于n，λ求偏导，则表示对关于n求偏导。

23、s3将区域ω进行网格划分(如三角形划分、矩形划分)，在网格划分后的离散区域内，求解线性方程(5)得到关于增量δn，δλ的近似值δnh，δλh。

24、对δn采用二阶拉格朗日有限元函数δnh∈vh来近似，对δλ采用一阶拉格朗日有限元函数δλh∈qh来近似，其中vh和qh分别为二阶、一阶拉格朗日有限元空间。线性方程(5)对应的矩阵表达式如下：

25、

26、其中，u表示δnh在二阶拉格朗日有限元空间vh中的系数向量，x表示δλh在一阶拉格朗日有限元空间qh中的系数向量，aγ，b分别对应于(5)式中的矩阵形式，bt对应于(5)式中的矩阵形式，f和g对应于(5)式中和的向量形式。下面针对方程(6)进行预处理器设计，从而保证在增广系数γ取较大值(如γ＞103)时有较快的计算速度，并且保持求解过程关于增广系数γ的稳健性(即，求解方程(5)时，牛顿迭代次数不随γ取值增大而迅速增大)。

27、s4为求解方程(6)，设计如下预处理器q-1：

28、

29、其中，i为单位矩阵，为矩阵aγ的逆，为矩阵aγ的schur补矩阵的逆，具体表示为：

30、

31、其中，表示拉格朗日乘子λ的质量矩阵逆，由经典的cholesky分解得到。

32、在使用预处理器q-1(如公式(7)所示)求解方程时，需对未知量的计算方式作进一步细化，即需要设计一个光滑器：基于网格划分，选取临近单元的自由度(即，在网格单元上的未知量)并将位于网格点上的自由度同时计算，然后利用初始猜测解n0＝[1，0，0]t和光滑器预先光滑；利用光滑器进行预先光滑时，为平衡计算量和计算速度的关系，预先光滑次数可选为3次；此过程中，光滑器的选择将影响预处理器q-1的效果，尤其是增广系数γ取值一般较大(本设计取γ∈[103，106])，容易造成计算的不稳健。因此需要设计保证计算关于模型参数稳健的预处理器，此时光滑器的选择与设计便极为重要。

33、选择任意满足核空间与子空间vi(i＝1，...，m)可以同时分解的有限元空间分解方式，即有限元空间分解满足

34、

35、其中在区域ω内几乎处处成立}，此时的预处理器便可保证其关于增广系数γ的稳健性。

36、s5根据s4设计的预处理器q-1，求解方程(6)，采用相对误差收敛条件(即，增量δnh，δλh的相对误差小于10-4)进行收敛判断，如果当前步骤k下方程(6)的求解满足相对误差收敛条件，则将当前步骤更新到k+1，得到nk+1，λk+1值，并重复s2-4，直到牛顿迭代法得到的近似值nk满足绝对误差小于10-8的绝对误差收敛条件。

37、与现有技术相比，本发明的有益效果是：

38、·设计的预处理器关于模型参数具有稳健性。由于采用的预处理器满足有限元空间分解的关键条件(公式(8))，可使得迭代次数不随增广系数的增大而明显增大。

39、·求解器更快速。由于该算法基于特殊光滑器的选择，可避免耗时计算，提高求解效率。

40、·本发明首次实现了针对非线性约束条件的极小化问题求解，不仅求解快速而且收敛特征符合预期。