一种双组分抛物线型系统跨尺度时空扩散的构建方法

本发明涉及仿真，具体的说是涉及一种双组分抛物线型系统跨尺度时空扩散的构建方法。

背景技术：

1、自微分方程理论诞生以来，偏微分方程一直发挥着重要的作用，广泛地出现在气象预报、海洋流动、环境治理、量子碰撞、航天计算、武器研究、飞机制造、交通涉及、水坝建设、油田开发、生物医学、股票期权等邻域，用于描述、解释或者预见各种自然现象、社会现象和科学工程问题。偏微分方程具有三大类型，分别包括抛物型、双曲型和椭圆型，对偏微分方程的深入研究，有助于我们更好地理解自然和社会现象中的各种变化规律。抛物型偏微分方程是理论中一个重要的分支，它描述了许多自然现象和工程问题中的物理过程，如反应扩散、热传导、物质运输等。近些年，反应扩散系统作为斑图生成系统引起了人们的极大兴趣。在数学上，反应扩散系统采用半线性抛物线型偏微分方程的形式，方程的解表现出广泛的行为，包括行波和类波现象的组成，以及其它自组织模式，如点状斑图、条形斑图、混合状斑图或更复杂的结构。这些奇妙的现象统称为“turing斑图”。

2、因此说，偏微分方程的求解技术是备受关注的研究内容。传统的求解技术需要精确地解析表达问题的通解，或者某些特定情形的特解。然而，大部分偏微分并不具备解析表达式。因此，利用解析表达式计算大量的时空位置的函数值，并不是高效的解决方案。随着计算机技术的蓬勃发展，简单便捷地数值求解越来越受到广泛学者的关注。相较于最简单的单组分反应扩散方程，双组分系统比单组分系统允许更大范围可能的丰富动力学行为。此外，大多数反应扩散系统的位置信息都是一维的。当从一个空间维度转向多个空间维度时，是否依然可以用来自一维系统的许多结论陈述，这是一个问题。故本专利设计一种双组分抛物型系统跨尺度时空扩散的构建方法,建立起抛物型系统在不同空间尺度下的时空动力学行为之间的关联。

技术实现思路

1、本发明所要解决的技术问题在于充实延伸了偏微分方程建模与仿真的研究领域，提出一种双组分抛物线型系统跨尺度时空扩散的构建方法，探究双组分抛物型系统更加丰富的动力学行为，建立抛物型系统在不同空间尺度下的时空动力学行为之间的关联。

2、本发明是通过以下技术方案来实现的，一种双组分抛物线型系统跨尺度时空扩散的构建方法，所述方法包括如下步骤：

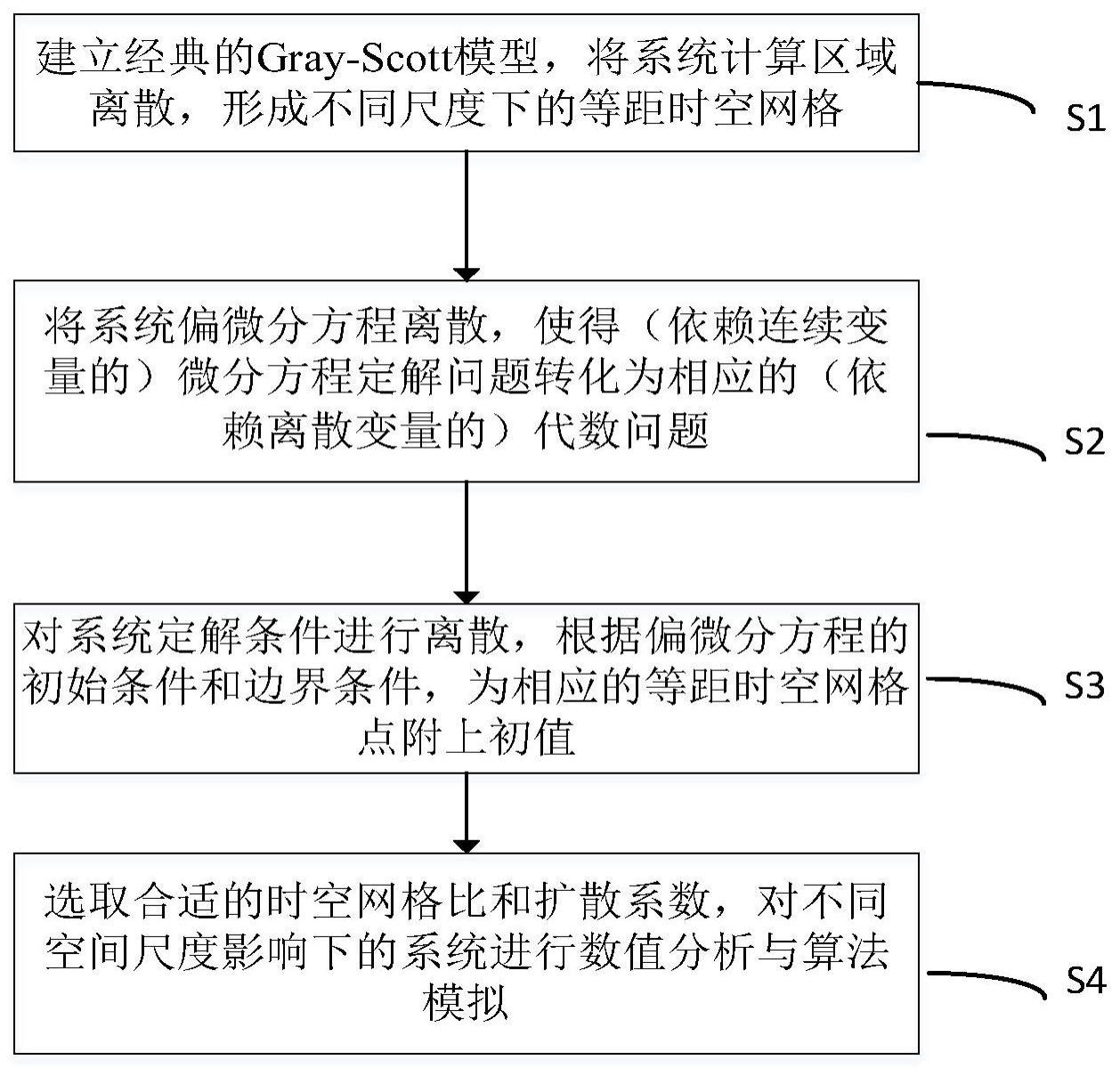
3、步骤1：建立一类经典的双组分抛物线型gray-scott系统，并针对不同的空间位置信息，对系统进行等距时空网格划分；

4、步骤2：利用taylor展开定理，对步骤1中所述的系统在不同空间尺度下的偏微分方程进行离散化处理，将依赖续变量的微分方程定解问题转化为相应的依赖离散变量的代数问题；

5、步骤3：根据系统在不同空间尺度下的偏微分方程的初始条件和边界条件，为相应的等距时空网格点附上初值；

6、步骤4：选取合适的时空网格比和扩散系数，利用matlab仿真软件，分别对不同空间尺度影响下的gray-scott系统进行数值分析与算法模拟，构建抛物性系统在不同空间尺度下时空动力学行为之间的关联。

7、优选的，步骤1所述的一类经典的双组分抛物线型gray-scott系统，其数学表达式为：

8、

9、

10、其中，表示拉普拉斯算子，u代表基底物，v代表催化剂，u和v代表两种化学物质，du和dv分别表示两种化学物质扩散系数，f代表物质u的进给率，k代表物质v的去除率。

11、优选的，步骤1所述的针对不同的空间位置信息，对系统进行等距时空网格划分，具体为：对于一维空间求解区域ω∈r，数值分析选取等距线段，对于二维空间求解区域ω∈r2，数值分析选取规则矩形，对于三维空间求解区域ω∈r3，数值分析选取规则立方体，且不同尺度的空间网格步长划分一致。

12、优选的，步骤2所述的将依赖续变量的微分方程定解问题转化为相应的依赖离散变量的代数问题，具体为：利用newton差商理论和taylor展开公式，对系统在不同空间尺度下的偏微分方程进行离散化处理，时间尺度采用一阶向前差商，空间尺度采用二阶中心差商。

13、优选的，步骤3所述的根据系统在不同空间尺度下的偏微分方程的初始条件和边界条件，为相应的等距时空网格点附上初值，具体为：对于一维空间扩散的初始条件，算法仿真模拟选取的初值为正弦函数，对于二维及三维空间扩散的初始条件，算法仿真模拟选取的初值为局部网格常数赋值；以上不同空间尺度下的系统的边界条件，均选取与外界零通量的neumann边界。

14、优选的，步骤4所述的选取合适的时空网格比和扩散系数，利用matlab仿真软件，分别对不同空间尺度影响下的gray-scott系统进行数值分析与算法模拟，具体为：利用离散最大模原理，即差分格式有凸组合系数结构。

15、进一步地，依据gray-scott系统的空间维度对计算区域进行划分，当系统的空间尺度为一维时，其数学表达式为：

16、

17、

18、x＝ωx∈[0,l],

19、对求解区域ωx进行以下离散化处理：

20、

21、其中，h称为空间步长，τ称为时间步长，l为空间轴长度，t为时间轴长度,l以h为步长等分为m份，t以τ为步长等分为n份；将真解u(x,t)限制在(m+1)×(n+1)离散网格上，相应的离散数据集合：

22、

23、当系统的空间尺度为二维时，其数学表达式为：

24、

25、

26、(x,y)＝ωxy∈[0,l]×[0,l],

27、对求解区域ωxy进行以下离散化处理：

28、

29、其中，h称为空间步长，τ称为时间步长，l为空间轴长度，t为时间轴长度,l以h为步长等分为m份，t以τ为步长等分为n份；将真解u(x,y,t)限制在(m+1)×(m+1)×(n+1)离散网格上，相应的离散数据集合为：

30、

31、当系统的空间尺寸为三维时，其数学表达式为：

32、

33、

34、(x,y,z)＝ωxyz∈[0,l]×[0,l]×[0,l],

35、求解区域ωxyz进行以下离散化处理：

36、

37、其中，h称为空间步长，τ称为时间步长，l为空间轴长度，t为时间轴长度,l以h为步长等分为m份，t以τ为步长等分为n份；将真解u(x,y,z,t)限制在(m+1)×(m+1)×(m+1)×(n+1)离散网格上，相应的离散数据集合为：

38、

39、

40、进一步地，利用taylor展开定理，对于步骤1中的系统偏微分方程进行离散化处理，将依赖续变量的微分方程定解问题转化为相应的依赖离散变量的代数问题。

41、当系统的空间尺度为一维时，取网格的空间步长为h，时间步长为τ，在(xi,tl)处，利用newton差商理论和taylor展开公式，时间导数离散为一阶向前差商，空间导数离散为二阶中心差商，可得：

42、

43、

44、其中i＝2,3…m,l＝1,2…n,略去无穷小量，进一步得到位置信息为一维的系统的偏微分方程离散化形式：

45、

46、

47、当系统的空间尺度为二维时，取网格的空间步长为h，时间步长为τ，在(xi,yj,tl)处，利用newton差商理论和taylor展开公式，时间导数离散为一阶向前差商，空间导数离散为二阶中心差商，可得：

48、

49、

50、其中i,j＝2,3…m,l＝1,2…n,略去无穷小量，进一步得到位置信息为二维系统的偏微分方程离散化形式：

51、

52、

53、当系统的空间尺度为三维时，取网格的空间步长为h，时间步长为τ，在(xi,yj,zk,tl)处，利用newton差商理论和taylor展开公式，时间导数离散为一阶向前差商，空间导数离散为二阶中心差商，可得：

54、

55、

56、其中i,j,k＝2,3…m,l＝1,2…n,略去无穷小量，进一步得到位置信息为三维系统的偏微分方程离散化形式：

57、

58、

59、进一步地，根据系统的偏微分方程的初始条件和边界条件，为相应的等距时空网格点附上初值。

60、位置信息为一维的系统的偏微分方程，数值初值定义为：

61、

62、

63、数值边界定义为：

64、

65、

66、其中，ux,vx为依赖一维位置信息的函数，ut,vt为依赖时间演化的函数；

67、位置信息为二维的系统的偏微分方程，数值初值定义为：

68、

69、

70、数值边界定义为：

71、

72、

73、其中，uxy,vxy为依赖二维位置信息的函数，ut,vt为依赖时间演化的函数；

74、位置信息为三维的系统的偏微分方程，数值初值定义为：

75、

76、

77、数值边界定义为：

78、

79、

80、其中，uxyz,vxyz为依赖二维位置信息的函数，ut,vt为依赖时间演化的函数；

81、进一步地，对于位置信息为一维的系统的扩散算法时空网格比和扩散系数满足对于位置信息为二维的系统的扩散算法时空网格比和扩散系数满足对于位置信息为三维的系统的扩散算法时空网格比和扩散系数满足

82、与现有技术相比，本发明具有以下显著的技术效果：(1)本发明一种双组分抛物线型系统跨尺度时空扩散的构建方法中设计了时空扩散算法相较于其他偏微分方程仿真算法，操作简便易行，考虑了更多位置信息，展现了双组分抛物型系统更丰富的动力学行为。

83、(2)本发明设计的时空扩散算法建立起抛物型系统在不同空间尺度下的时空动力学行为之间的关联。

84、(3)本发明中一种双组分抛物线型系统跨尺度时空扩散的构建方法中所设计的时空扩散算法具有较强的适用性，同样适用于其他的具有双组分抛物型格式的复杂动力学网络。

85、(4)本发明采用双组分抛物型系统多尺度时空扩散的算法构建的双组分抛物型系统，为单组分和多组分系统的算法仿真的设计与实现具有重要指导意义。