一种基于高斯混合模型的结构随机不确定性传播方法

本发明涉及随机不确定性传播，具体涉及一种基于高斯混合模型的结构随机不确定性传播方法。

背景技术：

1、随机不确定性的研究较早，以概率论中的概率模型作为不确定性建模的工具，有着较为成熟的理论基础和工程应用，如：用输入变量的均值、标准差、概率密度函数((probability density function，pdf下同)、累积分布函数(cumulative distributionfunction，cdf下同)等描述机械系统功率、电压等的波动。常用的随机不确定性传播方法大致可以分为以下几类：(1)基于样本的方法：典型方法包括无迹变换和蒙特卡罗仿真(mcs)。传统蒙特卡罗方法的主要思想是通过随机抽样的方式生成一组样本，然后计算每个样本点在功能函数上的值，最后对所有样本的结果进行分析以获得统计矩(均值、标准差、pdf)等。(2)局部展开法：第一类是基于均值点展开的均值一次二阶矩和二次四阶矩方法。由于在均值点展开有着精度低、不变性等问题，所以产生了第二类基于最可能点(mpp)展开的方法，主要有：一次可靠度方法(form)和二次可靠度法(sorm)。(3)数值积分法：首先根据输入变量的分布类型选择特定的求积公式求解功能函数的统计矩，然后基于最大熵方法或泊松(pearson)经验系统求解功能函数响应的概率密度函数。主要有全因子数值积分法(ffni)、单变量降维法(udrm)、稀疏网格数值积分法(sgni)。(4)随机展开法：主要有多项式混沌展开法(pce)。pce方法的理论基础为多项式混沌理论，当条件满足时，能够精确地表征任意形式随机变量的不确定性。(5)基于代理模型的方法：建立显式数值模型来替代隐式且耗时的功能函数，在此数值仿真模型的基础上可以更高效地计算响应的统计矩或概率分布函数，如人工神经网络(ann)、径向基函数(rbf)、支持向量回归(svr)、克里金(kriging)等。

2、但在现有技术中，普遍存在多个极值的高度非线性功能函数的可能会给出错误的拆分方向从而产生较大误差的问题。

技术实现思路

1、因此，针对输入变量为高斯分布或高斯混合模型以及存在多个极值的高度非线性功能函数的问题，本发明提供一种基于高斯混合模型的结构随机不确定性传播方法。

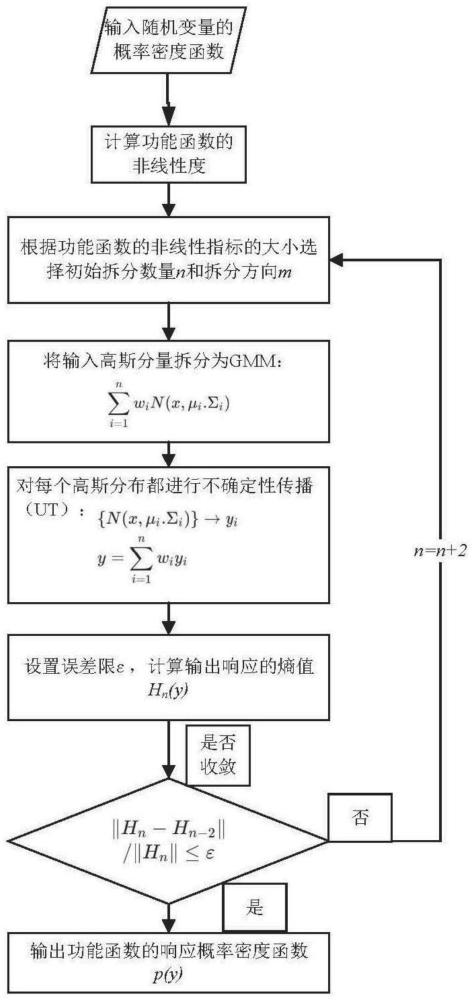
2、一种基于高斯混合模型的结构随机不确定性传播方法，该方法包括：

3、s1.对输入的高斯分量进行拆分；对高斯混合模型中的高斯分量进行拆分，并逐渐增加其拆分的数量，使得功能函数在拆分之后的高斯混合模型的每一个分量的局部范围内接近线性化，获得在经过非线性功能函数传播之后的响应pdf近似为高斯分布的小方差高斯分量；

4、其中，对于多变量高斯分布，提出基于功能函数的非线性与输入变量协方差对不确定性传播的影响的判断准则，并基于此判断准则计算功能函数的非线性指数，以确定多变量高斯分布的拆分方向和拆分个数；

5、s2.基于无迹变换(ut)进行小方差高斯分量的不确定性传播，获得响应的概率密度函数；

6、s3.建立收敛机制；分别计算相邻两次响应的概率密度函数的熵值之差，若相邻两次响应pdf的熵值之差小于预设误差值则输出响应pdf，否则增加拆分个数循环上述步骤。

7、在s1中，设随机变量x包含m个样本的数据集x，x＝(x(1)，x(2)，...x(m))；数据集x有n个样本点，总样本数量设为n，高斯混合模型的分量数设为k个，参数w表示n×k的矩阵，k表示第k个高斯分量；

8、则随机变量x的概率密度函数为高斯混合模型，表示为：

9、

10、其中，μk表示均值、∑k表示协方差；

11、对f(x)的第k个高斯分量进行拆分，用高斯混合模型来表示为：

12、

13、其中，l＞1，即将单个高斯分量k拆分为具有l个分量的高斯混合模型。j表示第j个分量，具有l个权值αk，j、l个均值μk，j、l个协方差∑k，j，

14、单变量高斯分布的拆分：针对标准单变量高斯分布p＝n(x；0，1)的拆分，将l设为奇数，施加如条件式(2)所示的约束，

15、

16、多变量高斯分布n(x|μ，∑)的拆分：对其协方差进行特征值分解：

17、∑＝vλvt    (3)，

18、v＝[v1，v2...，vm]，λ＝diag[γ1，γ2...，γm]    (4)；

19、其中，γm是协方差矩阵特征值，vm是特征值γm对应的特征向量，矩阵v为旋转矩阵；

20、将高斯分布作相应的线性变换，使随机变量x在变换后相互独立，线性变换的表达式如下：

21、

22、则变换之后的高斯概率密度函数为

23、

24、其中，i为单位矩阵，即协方差矩阵；

25、因高斯概率密度函数f(y)的协方差矩阵i为对角矩阵，那么协方差矩阵对应的特征向量分别与其坐标轴平行，所以应用单变量拆分库来对多变量高斯分布沿坐标轴方向进行拆分；

26、设高斯分布沿第z个坐标轴方向进行拆分：

27、

28、其中，上式中μk，σk分别表示第k个高斯分布的均值和标准差；

29、将公式(7)代入到公式(6)中，得到拆分后的多变量高斯混合模型：

30、

31、将高斯混合模型作线性变换将其旋转、平移、伸缩到初始高斯分布的坐标系空间中，获得拆分之后的多变量高斯混合模型(gmm)；

32、线性变换前后的权值wk不变，则拆分之后高斯分量的均值与协方差如下：

33、

34、

35、∑k＝vtλv    (9)

36、对于多变量高斯分布，有多个拆分方向，采用t值判断准则，并基于此判断准则计算功能函数的非线性指数，以确定多变量高斯分布的拆分方向m和拆分个数n；功能函数的非线性度表示为：

37、

38、其中，γ表示协方差矩阵∑的特征向量；h表示给定常数；是一个表示拆分的方向单位向量。

39、在s2中，由s1可知n维输入不确定性参数在经过拆分之后用高斯混合模型来表示：对高斯混合模型的第k个分量进行不确定性传播；

40、首先计算2n+1个sigma点的权重：

41、

42、式中：表示计算第k个高斯分量响应近似均值时的sigma点权重，表示计算第k个高斯分量响应近协方差时的sigma点权重，参数λ满足：

43、λ＝α2(n+t)-n    (12)；

44、其中，参数α和参数t为比例参数，控制sigma点的分布范围；α满足10-4≤α≤1，t≥0，β待选参数为一个非负的权参数；

45、设sigma点位于输入变量的均值处或对称分布于协方差的主轴上，从这些位置采样得到一组sigma点，并构成一个点集矩阵χ(i)，其计算方法为：

46、

47、其中，表示矩阵(n+λ)∑x作cholesky分解后下三角矩阵的第i-1列，表示下三角矩阵的第i-n-1列；

48、系统的功能函数为y＝g(x)，将每个sigma点代入到功能函数中，得到系统响应对应的点集y(i)＝g(χ(i))，则第k个高斯分量经过ut变换之后的均值与协方差如下：

49、

50、在使用无迹变换对拆分后的高斯分量进行不确定性传播时，假定传播过程中高斯分量的权值保持不变，即wy，k＝wk；同时高斯分量经过功能函数之后，依然保持为高斯分布，则系统响应的概率密度函数为：

51、fy(y)＝∑wkn(y；μy，k，∑y，k)    (15)。

52、在s3中，通过该收敛机制可以逐步提高系统响应概率密度函数的精度，直到满足所要求的不确定性传播精度；

53、采用以热力学中的香农熵用来描述整个系统的不确定性；对于个连续随机变量x，其香农熵定义如下：

54、

55、其中，ω是概率密度函数p(x)的定义域；当随机变x服从高斯分布p(x)＝n(x，μ，∑)，信息熵存在解析解：

56、

57、当为高斯混合模型时，香农熵的表达式如下：

58、

59、对于概率分布为高斯混合模型的情形，采用近似求值法对其香农熵的值进行估计：

60、

61、其中，h(x|c)为条件熵，bd(pi||pj)为巴氏距离，具体如下：

62、

63、

64、当前后两次响应pdf的熵值不大于预设误差限ε，则为满足收敛条件，输出最终的响应pdf，即输出此时功能函数响应的概率密度函数p(x)。

65、在s3中，当前后两次响应pdf的熵值大于预设误差限ε，则增加拆分个数，取n＝n+2，再次循环。

66、本发明技术方案，具有如下优点：

67、本发明针对输入变量为高斯分布或高斯混合模型以及存在多个极值的高度非线性功能函数的问题，首先提出判断准则，用于计算功能函数在输入高斯分量各个方向上的非线性度，并根据非线性度的大小，将输入高斯分量进行拆分，用方差更小的高斯混合模型来表示；然后，对小方差的高斯分量基于ut变换进行不确定性传播；最后，同时计算响应pdf的熵值，当两次响应pdf的熵值差小于给定误差限时，输出最终响应的pdf。

68、本发明相较于传统的基于概率的不确定性传播方法有着很高的计算精度，同时适用范围更加广泛，优势明显；同时，本发明方法可拓展性强，可以同其他不确定性传播方法相结合，且理论上可以拓展到任意输入分布。