一种用有限梁类比无限粘弹性地基梁的方法

本发明涉及轨道模型评估领域，尤其是涉及一种用有限梁类比无限粘弹性地基梁的方法。

背景技术：

1、如何更好的揭示列车-轨道耦合系统的动力响应机制，一直是目前最重要的研究课题之一。之前的研究中，通常将轨道视为winkler地基梁，而将列车车轮对轨道的作用简化为移动力。虽然此种简化模型一定程度上给出轨道响应的基本特征，但也存在一些不吻合实际的情况，如当外部荷载以临界速度通过地基梁时，梁位移响应将无限持续。显然这种现象不符合实际，因任何动力系统都存在阻尼，从而耗散外部输入的能量。

2、另外，从既有研究来看许多学者大多将移动荷载作为一恒定的常力荷载，忽略了外部荷载的频率。事实上，因轨道不平顺的激励以及列车自身的机械运动，列车运动所产生的移动荷载幅值会随时间而变化。特殊情况下，当外部移动荷载频率和轨道频率接近时，还容易诱发轨道的共振。因此，在车-轨系统动力响应分析时，除了研究等振幅的移动荷载外，还需要考虑幅变移动荷载对无限长地基梁动力响应的影响，目前该问题尚未得到封闭解。从实际的角度来看，使用无限梁来模拟轨道响应并不是一种非常有效的方法，人们利用有限梁模拟无限梁的振动进行了一些研究，但忽略基础阻尼的影响。

3、因此，有必要提供一种用有限梁类比无限粘弹性地基梁的方法，来解决上述问题。

技术实现思路

1、本发明的目的是提供一种用有限梁类比无限粘弹性地基梁的方法，利用留数定理和格林函数，给出了位于粘弹性基础上的无限梁uic轨道在移动简谐荷载下的动态响应的封闭解，用模态叠加法给出了类似有限梁的封闭解，用有限元法验证了两种解析解的准确性；基于解析解进行参数研究，得到最能模拟无限梁uic轨道的模拟有限梁的跨度长度。

2、为实现上述目的，本发明提供了一种用有限梁类比无限粘弹性地基梁的方法，包括以下步骤：

3、s1：利用格林函数，推导出无限粘弹性地基梁在移动简谐荷载下的动态响应的封闭解；

4、s2：用模态叠加法推导出类似有限梁的封闭解；

5、s3：利用有限元方法验证无限梁和有限梁理论推导的正确性；

6、s4：对解的正确性进行数值验证。

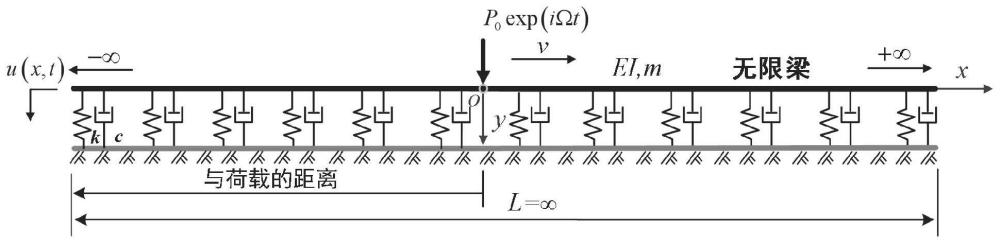
7、优选的，在步骤s1中，简谐荷载在无限梁上以速度v移动，粘弹性地基单位长度的刚度和阻尼系数分别由k和c表示，通过力学模型模拟的无限地基梁，梁在t时刻的x截面的运动方程为：

8、

9、其中，u(x,t)表示梁为y方向的位移，e为弹性模量，i为惯性矩，m为单位长度的质量；对于温克勒基础，k为刚度，c为粘性阻尼系数，f(x,t)为简谐荷载，表示为：

10、f(x,t)＝p0 exp(iωt)δ(x-vt)  (2)

11、时，p0和ω分别表示外部荷载的振幅和频率，δ(·)为狄拉克函数；

12、利用delta函数的属性，函数f(x)表示为：

13、

14、对函数f(x,t)进行傅里叶变换及其逆变换：

15、

16、

17、以及运用傅里叶变换的以下性质：

18、f[f(n)(t)]＝(iω)nf[f(t)]  (6)

19、基于格林函数的定义，引入格林函数g(x,t,x0,t0)，式(1)中的偏微分方程转化为：

20、

21、其中fδ(x,t；x0,t0)表示单位源函数，

22、fδ(x,t；x0,t0)＝δ(x-x0)δ(t-t0)  (8)

23、其中x0和t0分别表示源函数的空间坐标和时间坐标；

24、对式(7)进行二重傅里叶变换得，

25、

26、其中，是格林函数g(x,t,x0,t0)的傅里叶变换，是格林函数fδ(ξ,ω；x0,t0)的傅里叶变换，对式(8)进行二重傅里叶变换得到：

27、

28、将式(10)代入到式(9)中，得到格林函数在频域内的解：

29、

30、通过对式(11)进行二重傅里叶逆变换，得到格林函数在时域内的解：

31、

32、对于外部荷载f(x,t)，式(1)的解通过对格林函数在全域内积分得到位移响应：

33、

34、将式(12)代入式(13)得：

35、

36、其中分别代表相对刚度、阻尼和质量；

37、狄拉克函数的傅里叶变换和逆变换表示为：

38、

39、

40、利用式(15)、(16)及delta函数的性质式(3),位移响应式(14)进一步表示为

41、

42、由式可知，式(17)是一个复数函数,为了便于分析，解只考虑实数部分，利用留数定理求解式(17)之前，首先求解分母特征方程的根即：

43、

44、根据代数基本定理，特征方程(18)包含实根、虚根和复数根。

45、优选的，实根存在性条件，实根设为ξ＝ξ0，ξ0≠0，，ξ0∈r，将其代入式(18)得

46、

47、式(19)实部和虚部应满足以下方程组：

48、

49、式(20a)求解为：

50、用式(21)代入到式(20a)得到：

51、式(22)证明实根存在的条件无效，因此式(18)不存在实根；

52、虚根的存在性条件：将参数和虚根ξ＝iξ1，ξ1≠0,ξ1∈r，代入式(18)中，得到式(23)，

53、

54、下面的方程组适用于式(23)为有效的情况：

55、

56、首先求解式(24b)得：

57、将式(25)代入式(24a)得到式(26)：

58、

59、当式(26)存在一个解时，虚根才会存在，ω≠0时，粘弹性地基上无限梁在移动简谐荷载作用下的计算结果表明式(19)只存在复数根；

60、复数根的存在性条件：复数根表示为ξ＝ξa+iξb，ξa,ξb≠0，ξa,ξb∈r，将代入式(18)令实部和虚部等于零，得到以下方程：

61、

62、利用matlab平台中内置的留数功能得到复数根的分布，其中两个位于实轴re(ξ)的上半平面，而另外两个位于下半平面，且不存在重根；

63、为了求解式(17)的位移响应，使用留数定理，它包含两个部分：一个是移动荷载前，x-vt≥0，梁的位移响应，另一个是移动荷载后，x-vt＜0，梁的位移响应；

64、x-vt≥0时，位移响应u(x,t)表示为：

65、

66、其中im(·)表示复变量ξ的虚部，res{·}为括号内留数的计算，式(28)中包含两个术语，第一项im(ξ)＞0表示与位于ξ上半平面中与复数根相关的位移，第二项im(ξ)＝0表示位于实轴上与实根相关的位移，特征方程(19)在复平面中ξ中当ω≠0时仅包含四个一阶极点且没有重根，实根已被证明不存在，因此当x-vt≥0，式(28)一阶极点的留数为：

67、

68、通过联立式(28)和(29)，x-vt≥0时无限梁位移响应u(x,t)为：

69、

70、对于x-vt＜0时，位移响应u(x,t)通过类似的方法求得，仅需考虑位于ξ下半平面上的复数根，即im(ξ)＜0，位移响应u(x,t)表示为：

71、

72、所有的情况都得到了对应的解，移动简谐荷载产生的波沿梁向两个相反的方向传播，并且在弹性基础上的移动荷载两侧的位移曲线是对称的。

73、优选的，在步骤s2中，寻找最适合有限梁跨度，以模拟无限梁的位移响应，利用模态叠加的方法，有限简支梁的位移u(x,t)近似表示为：

74、

75、其中qb,n(t)为广义模态坐标，将式(32)代入式(1)中，等式两边分别乘以sin(nπx/l)，并关于x从0到l进行积分，得到模态方程式(33)：

76、

77、其中ωb,n为粘弹性基础上梁的第n个无阻尼频率，εn为阻尼比；

78、

79、利用三角函数关系，式(33)重新表示为：

80、

81、其中，ωdl,n和ωdr,n分别为有限梁左、右移频率，ωdl,n＝ω-nπv/l，ωdr,n＝ω+nπv/l；在式(35)解中包括稳态响应和瞬态响应，稳态响应由外部荷载所引起，瞬态响应由初始条件，所决定，梁的位移响应u(x,t)表示为：

82、u(x,t)＝sb,n(x,t)+tb,n(x,t)  (36)

83、其中，sb,n(x,t)和tb,n(x,t)分别为稳态响应和瞬态响应；

84、经过求解，梁位移稳态响应sb,n(x,t)表示为：

85、

86、其系数为：

87、式中，wn为由施加的静力荷载所引起的位移，ηr,n和ηl,n为与频率相关的系数；

88、

89、式中，βln和βrn为两个频移成分与第n个有限梁固有频率的比值，βln＝ωdl,n/ωbn，βrn＝ωdr,n/ωbn；

90、根据阻尼比εn大小，瞬态响应分为以下三种情况：

91、0＜εn＜1时，

92、

93、

94、其中，ωd,n表示梁的第n个阻尼频率，表示为

95、εn＝1时

96、

97、

98、εn＞1时

99、

100、有限梁稳态响应式(37)中包含两个频移成分：ωdl,n＝ω-nπv/l，ωdr,n＝ω+nπv/l，和固有频率ωb,n，根据式(30)和(31)得，无限梁中仅存在一阶固有频率。

101、优选的，在步骤s3中，无限梁元件由左半无限单元、一般单元和右半无限单元三部分组成，对于右半无限单元，其刚度、质量和阻尼矩阵分别为：

102、

103、

104、

105、其中{n}表示梁单元的形函数，右上角符号表示对坐标的导数，形函数{n}分别由{n1 n2}垂直自由度和旋转自由度相关的两个项组成，由弹性地基梁精确位移曲线来确定,如下所示，

106、对于弹性地基梁，位移的齐次微分方程表示为：

107、v″″+4λ4v＝0  (48)

108、其中，λ4＝k/4ei，为保证梁在无限远处转角和位移为零，对式(48)求解，得到(49)，

109、

110、通过将节点o处的边界条件设置为v(0)＝1v'(0)＝0，求解式(49a)得到的形状函数n1的表达式为：

111、

112、另一个形状函数通过将边界条件设置为：v(0)＝0v'(0)＝1，得到形函数n2表达式为：

113、

114、将式(50)、(51)代入式(45)～(47)所得到右半无限单元刚度、质量和阻尼矩阵分别为：

115、

116、左半无限单元求解过程与右半无限元素过程相同，除了梁在左端延伸到无穷远，所求得左半无限单元的单元刚度、质量和阻尼矩阵分别为：

117、

118、对于有限长度le的一般元素，将三次哈密顿插值函数代入方程(45)～(47)中，得到单元刚度、质量和阻尼矩阵分别为：

119、

120、

121、构建整个梁的全局运动方程：式中，mb、cb和kb分别为有限或无限梁的整体质量、阻尼和刚度矩阵；fb为力向量；和{ub}分别表示加速度、速度和位移向量，采用newmark-β方法，β＝0.25，γ＝0.5，在时域上逐步计算梁的动态响应。

122、优选的，在步骤s4，数值验证包括对封闭解的收敛性研究，解析解与数值解的比较和有限梁和有无阻尼的无限梁的比较。

123、因此，本发明采用上述一种用有限梁类比无限粘弹性地基梁的方法，具备以下有益效果：

124、(1)本发明无限有限梁和模拟有限梁的封闭解与有限元结果吻合较好，表明推出的理论和无限有限梁采用的有限元模型的有效性。

125、(2)本发明利用留数定理和格林函数，给出了位于粘弹性基础上的无限梁uic轨道在移动简谐荷载下的动态响应的封闭解。

126、(3)本发明用模态叠加法给出了类似有限梁的封闭解。

127、(4)本发明用有限元法验证了两种解析解的准确性。

128、(5)本发明基于解析解进行参数研究，得到最能模拟无限梁uic轨道的有限梁跨长。

129、下面通过附图和实施例，对本发明的技术方案做进一步的详细描述。