基于光滑粒子法的管道液柱分离的模拟方法及其设备与流程

本发明涉及输水工程水力学数值模拟领域，具体涉及基于光滑粒子法的管道液柱分离的模拟方法及其设备。

背景技术：

1、当输水管道系统中液体压力降低到汽化压力时，可能发生瞬变蒸汽空化现象。这些空化泡可能发育长大到占据整个管道截面的程度，破坏液柱的连续性。bergant和simpson等学者在文献中指出分离的液柱再弥合可能产生突升的高压脉冲，导致水力系统破坏。因此，为避免液柱分离现象，需对该现象进行严格的瞬变分析。

2、几十年来，很多学者采用各种方法来预测液柱分离过程中的瞬变压力，应用最广的是由streeter和wylie基于特征线法(moc，method of characteristics)以及周领基于有限体积法godunov格式(fvm，finite volume method)提出的离散气体—空穴模型(dvcm，discrete vapor-cavity model)，该模型允许气穴在压力达到或低于汽化压力的任何计算节点形成，并且作为一内部边界占据整个管道截面，因该模型易于嵌入到标准的水锤商业包中，且再现了液柱分离过程中很多的物理特性，已成为目前模拟液柱分离现象最常用的模型。

3、bergant和simpson于1995年设计搭建了如图1所示的实验系统来研究水液柱分离现象。整个系统包括上游水库1、输水管道2和阀门3组成。管道总长37.2m，内径22.1mm，管道倾角3.2°。水锤波速为1319m/s。伴随液柱分离的水锤事件由突然关闭下游阀门引起。实验工况参数见表1。

4、表1

5、

6、然而moc-dvcm方法的主要缺点是当采用相对细密的网格时，计算结果会出现虚假的压力脉冲，导致计算结果出现较大偏差；fvm-dvcm方法的主要缺点是，在气穴溃灭时的压力会出现高频压力振荡，导致计算结果精度不足。

7、因此，亟需提出一种新的方法来解决上述问题。

技术实现思路

1、本发明提供了基于光滑粒子法的管道液柱分离的模拟方法及其设备，来解决现有moc-dvcm方法存在的虚假脉冲的不足，以及fvm-dvcm方法存在的高频振荡的的问题。

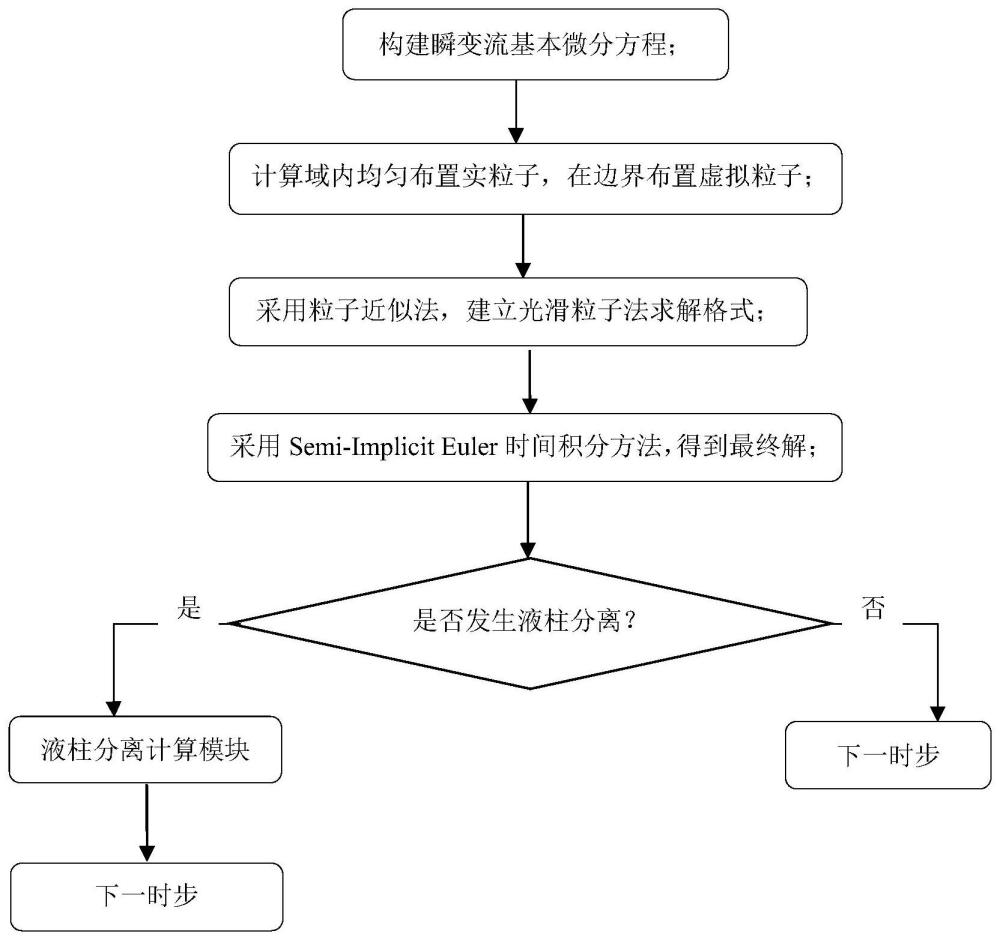
2、本发明提供了基于光滑粒子法的管道液柱分离的模拟方法，包括以下步骤：

3、建立管道瞬变流基本微分方程，根据待模拟的输水工程实例确定计算域、采集初始参数并确定边界条件；

4、在所述计算域内均匀布置实粒子，在边界处布置虚拟粒子；

5、采用粒子近似法，通过所述管道水力瞬变流基本微分方程，建立光滑粒子法的求解格式；

6、基于所述光滑粒子法的求解格式，通过半隐式欧拉时间积分方法，得到下一时步每个粒子对应的位置、压力和速度；

7、基于所述下一时步粒子的压力判定是否发生液柱分离：若已发生，则进行液柱分离模块计算；反之，进入下一时步计算，直至发生液柱分离，进行液柱分离模块计算。

8、进一步地，所述初始参数包括：初始入口压力，入口速度，管道长度和管道内直径；边界条件包括：上游为水库，压力进口；下游末端为阀门，且阀门瞬时关闭。

9、进一步地，所述管道瞬变流基本微分方程为：

10、

11、

12、其中，沿管线距离x与时间t是自变量；p(x,t)是测压管压力；v(x,t)是平均截面速率；g是重力加速度；c是波速；λ为达西-威斯巴哈摩阻系数；ρ为水体密度；d为管径。

13、进一步地，上游水库处布置的虚拟粒子的场变量与上游第一个实粒子的场变量一致，所述场变量包括测压管压力和平均截面速率；

14、下游阀门处布置的虚拟粒子的场变量为：

15、vim＝-vi              (3)

16、pim＝pi (4)

17、其中，上标m代表第i个实粒子对应的虚拟粒子；pi是第i个实粒子的测压管压力；vi是第i个实粒子的平均截面速率。

18、进一步地，所述建立光滑粒子法的求解格式包括以下步骤：

19、根据光滑粒子法，流动变量f的积分表达式为：

20、

21、其中，ω是计算域，是x与x′处两粒子的变量f的导数；是光滑函数w的导数；h是定义光滑函数w的影响区域的光滑长度；

22、光滑函数w(x-x′,h)使用三次样条光滑函数，函数方程如下：

23、

24、其中，r是点x与x′处两粒子之间的相对距离；α的值在一维、二维、三维空间中分别为

25、将计算域ω离散成有限数量(n)的，具有独立质量、密度的粒子，采用粒子近似法，对粒子i，建立流动变量f的粒子导数离散方程为：

26、n＝l/dx                            (7)

27、

28、其中，n是粒子总数；l为计算区域长度；dx为相邻粒子的间距；mj与ρj分别代表粒子j的质量与密度；h是光滑长度；是流动变量f的导数；是光滑函数w的导数；

29、通过所述管道水力瞬变流基本微分方程，建立光滑粒子法的求解格式为：

30、

31、

32、进一步地，通过半隐式欧拉时间积分方法，得到下一时步每个粒子对应的位置、压力和速度包括：

33、

34、

35、

36、其中，△t是时间步长；pin+1与pin分别是粒子i在n+1和n时步的测压管压力；vin+1与vin分别是粒子i在n+1和n时步的平均截面速率；和分别表示粒子i在n+1和n时步的位置。

37、进一步地，所述基于所述下一时步粒子的压力判定是否发生液柱分离包括以下步骤：

38、假定气穴仅在相邻粒子中部形成，当为纯水锤流动时，粒子i的压力和流量均通过光滑粒子法计算；

39、一旦任一粒子的压力达到或低于液体汽化压力，则粒子i的流量依然采用光滑粒子法求得,粒子i的压力则通过相邻粒子气穴的体积差值计算：

40、

41、

42、其中，分别为第i个粒子在n+1和n时步的气穴体积；a是管道截面积；是绝对汽化压力，为常数，是粒子i发生液柱分离后的压力；

43、一旦任一粒子的气穴体积小于或等于0，则气穴溃灭，流动恢复为纯水锤,压力和流量再次均由光滑粒子法计算。

44、进一步地，所述下一时刻粒子的压力小于等于液体汽化压力时，则判定认为发生液柱分离。

45、本发明还提供一种设备，包括：

46、存储器，用于存储计算机程序；

47、处理器，用于执行所述计算机程序时实现上述方法步骤。

48、相比于现有技术，本发明的有益效果为：

49、1、本发明提供了一种算法简单，易于实现的模拟方法，结合了粒子近似法和时间积分方法，克服了光滑粒子法在追踪气穴并预测其发育、溃灭方面的难题，可以满足计算粒子足够多时不会出现不真实的脉冲峰值和高频振荡，提高了计算精度；

50、2、本发明采用布置较多的粒子进行计算时，相对于传统网格方法(mov、fvm)使用较细密网格，计算结果不会出现虚假脉冲即高频振荡，提高了预测液柱分离过程中的瞬变压力的计算精度；

51、3、本发明的计算方法通过半隐式欧拉时间积分方法，为模拟多维水锤瞬变提供了框架，而moc、fvm解较难扩展到包含多维瞬变的流体问题。