包含数字控制延时的并网电流环临界阻尼参数确定方法与流程

本发明涉及电力电子技术领域，特别是一种包含数字控制延时的并网电流环临界阻尼参数确定方法。

背景技术：

并网变流器在电力系统有着极其广泛的应用，典型包括可再生能源(光伏、风电等)并网发电、电能质量治理、储能变流器、pwm整流等，此时变流器相对电网而言为一个等效的可控电流源，通过调节注入电网电流的幅值与相位，实现并网有功与无功功率调节的目的，因此变流器控制的重点是并网电流质量。

比例-积分(proportional-integral，pi)控制器在控制领域有着非常广泛的应用，由于基波正序交流信号在正序同步旋转坐标系(ps-srf)表现为直流量，因此直观上通过pi控制器对直流分量提供的无穷大增益，便可实现对ps-srf直流信号的无静差调节，因此基于srf的pi控制已经成为并网型变流器以及电机驱动等系统电流调节的工业标准长达20多年。

然而，被控对象在srf会出现交叉耦合项，使得d、q轴电流的暂态调节响应相互影响，即d轴电流的调节过程会影响q轴电流，反之亦然。将电网电压作为扰动分量考虑，则系统表现为一个两输入/两输出系统，其矩阵方程不利于使用常规的分析工具(如根轨迹、频率响应等)展开研究，也不利于控制器参数的调节。并且，对于数字控制而言，延时毕竟是不可忽略的，尤其是当控制频率相对于开关频率较高时(载波比低下的情况)，延时成为制约控制器性能的主要因素。

此外，pi控制器的参数调节长久以来是个谜一样的问题，缺乏统一而明确的指导依据。通常来说对控制器的性能要求可以分为两大部分，即对参考给定信号的跟踪能力(调节时间、超调、稳态误差等)以及对扰动信号的抑制能力(电网电压、电机反电势)。对于给定参考信号，期望并网电流尽可能快速跟踪参考信号的变化，并且尽可能减小超调，以避免变流器发生瞬时过流保护，这对于大功率变流器尤为重要，以此可以减小变流器启停机以及电流突变情况下对电网的冲击。

到目前为止，有关并网变流器电流环参数确定或者直接忽略耦合项的影响，或者使用状态反馈进行近似解耦。并且，没有考虑数字控制的一拍延时以及变流器所固有的临界保持特性，在大功率变流器受功率器件散热要求而开关频率低下的情况下，电流环性能下降，系统容易发生震荡甚至不稳定现象。此外，对于ps-srf的控制器增益确定缺乏明确的指导依据，更多地应用凑试法或者经验估计，难以实现变流器性能最优化，表现出电流阶跃响应超调量大且调节时间长的不足，容易引发变流器过流保护并对电网产生瞬时冲击。

技术实现要素：

本发明的目的在于提供一种包含数字控制延时的并网电流环临界阻尼参数确定方法，使得电流环阶跃响应调节时间最小的同时抑制超调的产生，从而使系统获得最高的稳定裕度。

实现本发明目的的技术解决方案为：一种包含数字控制延时的并网电流环临界阻尼参数确定方法，包括如下步骤：

(1)建立被控对象在正序同步旋转坐标系的矢量模型；

(2)以复系数矢量控制器的零点消除被控对象的复数极点，并通过延时补偿消除延时项在控制频率处的延时；

(3)将补偿后延时项以二阶pade函数展开；

(4)通过根轨迹曲线，得到系统处于临界阻尼状态的控制器增益。

进一步地，步骤(1)所述被控对象在正序同步旋转坐标系的矢量模型为：

其中，l为并网滤波器的滤波电感值，rl为滤波器与功率器件的损耗等效电阻，ωe为电网角频率，s是拉普拉斯变换因子。

进一步地，步骤(2)所述的复系数矢量控制器即为：

其中，k为控制器增益，为并网滤波电感估计值，为滤波器与功率器件的损耗等效电阻估计值，ωe为电网角频率，s是拉普拉斯变换因子。

进一步地，步骤(2)所述的延时补偿即为：

其中，td＝1.5·ts，且ts为采样时间。

进一步地，步骤(3)所述的二阶pade函数展开为：

其中，td＝1.5·ts，且ts为采样时间。

进一步地，步骤(4)所述根轨迹曲线所需的电流环开环传递函数为：

其中，k为控制器增益，td＝1.5·ts，且ts为采样时间。

本发明与现有技术相比，其显著优点为：(1)在临界阻尼控制器增益作用下，实现了电流参考给定最佳跟踪效果，即阶跃响应调节时间最小且没有发生超调；(2)使得电流环稳定裕度最高，消除了变流器瞬时过流的风险并有助于减小对电网的冲击，为变流器稳定运行提供保障；(3)为数字控制并网变流器电流环的增益提供了一种简便直观的确定方法。

附图说明

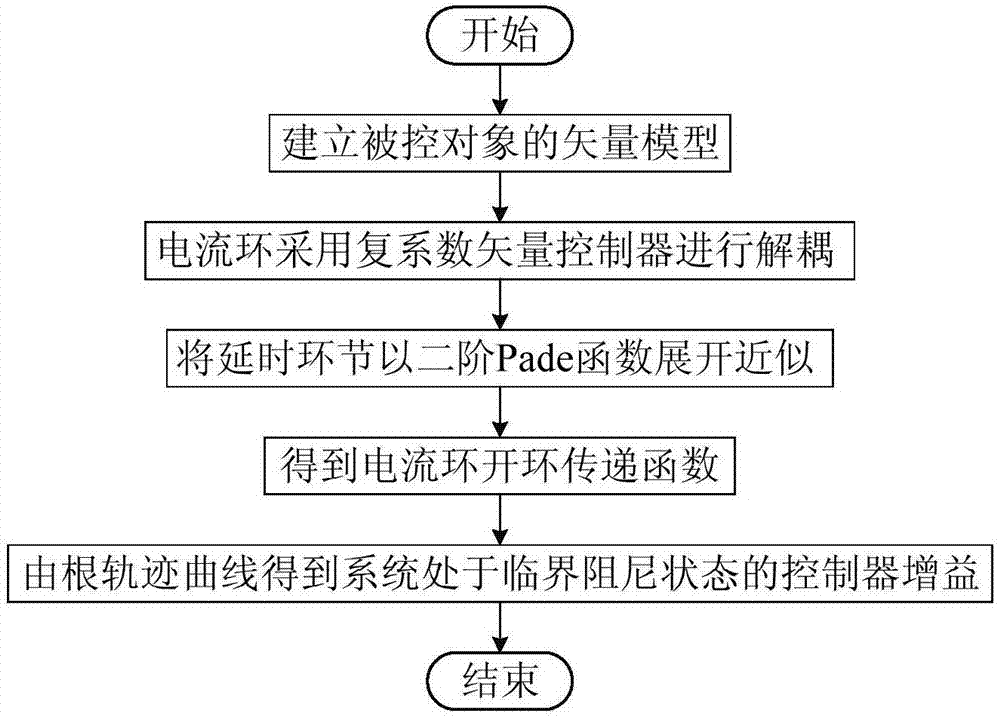
图1为本发明包含数字控制延时的并网电流环临界阻尼参数确定方法的流程图。

图2为并网型变流器主电路拓扑图。

图3为单电感并网变流器矢量模型图。

图4为电流环方框图。

图5为延时项延时补偿效果图。

图6为电流环延时补偿效果图。

图7为电流环根轨迹曲线—过阻尼状态图。

图8为电流环根轨迹曲线—临界阻尼状态图。

图9为电流环根轨迹曲线—欠阻尼状态图。

图10为电流环根轨迹曲线—临界稳定状态图。

图11为扫描控制器增益得到阶跃响应的调节时间与超调量关系图。

图12为临界阻尼与欠阻尼状态下电流环阶跃响应图。

图13为临界阻尼控制器增益电流环突增电流实验波形图。

图14为临界阻尼控制器增益电流环突增电流实验结果q轴电流图。

具体实施方式

下面结合附图对本发明作更进一步的说明。

本发明包含数字控制延时的并网电流环临界阻尼参数确定方法，以单电感并网变流器为被控对象，得到其在正序同步旋转坐标系的矢量模型，电流环采用复系数矢量控制器以抵消被控对象的复系数零点。以数字控制为出发点，在电流环直接包含由数字控制而引入的一拍延时。通过将该延时环节以二阶pade函数近似展开，进一步得到电流环开环传递函数。最后，通过分析电流环根轨迹曲线，找到使得系统处于临界阻尼状态的控制器增益作为电流环最优增益。本发明为数字控制并网变流器电流环的增益提供了一种简便直观的确定方法，在临界阻尼控制器增益作用下，电流环阶跃响应调节时间最短并且不会产生超调，以及获得了最高的系统稳定裕度，消除了变流器瞬时过流的风险并有助于减小对电网的冲击。

结合图1，本发明包含数字控制延时的并网电流环临界阻尼参数确定方法，包括如下步骤：

(1)建立被控对象在正序同步旋转坐标系的矢量模型；

(2)以复系数矢量控制器的零点消除被控对象的复数极点，并通过延时补偿消除延时项在控制频率处的延时；

(3)将补偿后延时项以二阶pade函数展开；

(4)通过根轨迹曲线，得到系统处于临界阻尼状态的控制器增益。

进一步地，步骤(1)所述被控对象在正序同步旋转坐标系的矢量模型为：

其中，l为并网滤波器的滤波电感值，rl为滤波器与功率器件的损耗等效电阻，ωe为电网角频率，s是拉普拉斯变换因子。

进一步地，步骤(2)所述的复系数矢量控制器即为：

其中，k为控制器增益，为并网滤波电感估计值，为滤波器与功率器件的损耗等效电阻估计值，ωe为电网角频率。

进一步地，步骤(2)所述的延时补偿即为：

其中，td＝1.5·ts，且ts为采样时间。

进一步地，步骤(3)所述的二阶pade函数展开为：

进一步地，步骤(4)所述根轨迹曲线所需的电流环开环传递函数为：

下面结合具体实施例对本发明进一步详细说明。

实施例1

如图2所示为并网变流器主电路拓扑，其中变流器输出接单电感滤波器l，并且rl为滤波器以及功率管损耗等效电阻，ea、eb、ec分别为a、b、c三相电网电压，而ia、ib、ic为三相并网电流，最后vdc为直流母线电压。其中控制流程如下，检测电网线电压eab与ebc并送入锁相环pll模块，得到基波正序电网电压的相位θ，并进一步将三相并网电流转换到ps-srf坐标系并得到id、iq分量。通过将参考电流分别与实际电流的id、iq分量相减，并将误差分量送入复系数矢量电流控制器，控制器的驱动即为变流器调制波分量，最后通过载波或者矢量调制算法得到功率管的驱动信号。

如图3所示为并网型变流器在ps-srf的矢量模型，其中edq＝ed+j·eq为电网电压在ps-srf的d、q轴分量，υdq＝υd+j·υq为调制波在ps-srf的d、q轴分量，idq＝id+j·iq为并网电流在ps-srf的d、q轴分量。

如图4所示为电流环在ps-srf的控制框图，其中为复系数矢量控制器，为延时补偿项，为延时项，而为被控对象矢量模型，为延时补偿与延时项的合并。如图5、图6所示为延时补偿效果图，延时补偿可以消除延时项在控制频率500hz处的相位滞后，如图5所示。另外，如图6所示，延时补偿后电流环开环频率相频响应在控制频率处的相位从90°突变为-90°，系统获得了可能的最高稳定裕度。

将图4所示(即用二阶pade函数近似展开)，进一步结合即可得到电流环开环传递函数为，得到电流环根轨迹曲线如图7、图8、图9、图10所示，其中系统分别处于过阻尼、临界阻尼、欠阻尼以及临界稳定状态。

如图7所示，闭环极点与均处于实轴，因此系统处于ξ＞1的过阻尼状态，阶跃响应呈现严格单调上升特点，不会产生超调。然而，如果进一步增大控制器增益，则闭环极点将进一步远离虚轴，从而加快响应速度。如图8所示，此时闭环极点均处于汇合点h2，而极点更加远离虚轴，因此可以忽略极点的影响，此时系统处于ξ＝1临界阻尼状态。如果进一步增大控制器增益，则闭环极点迅速向虚轴靠近，因此系统稳定性下降，并且响应速度减慢，阶跃响应伴随超调的产生，如图9所示ξ＜1的欠阻尼状态。此外，入股9所示，此时闭环极点处于虚轴，因此系统处于ξ＝0临界稳定状态，如果进一步增大控制器增益，闭环极点将最终处于右半平面，从而导致系统不稳定。

由此可见，ξ＝1对应的控制器增益kopt将使得电流环获得最好的暂态性能与稳定性，首先闭环主导极点的位置与虚轴最远并且均位于实轴，因此阶跃响应获得了最快的响应速度并且不会产生超调，并且由于闭环极点与虚轴距离最大也意味着系统的稳定性最好。

设置开关频率分别为3khz、5khz与10khz，设置控制器增益从零开始逐渐增大，并求出所有控制器增益对应的电流环阶跃响应所对应的调节时间与超调量，得到两者的关系曲线如图11所示。可见在所考虑的开关频率，当控制器增益去临近阻尼增益kopt时，电流环阶跃响应的确没有产生超调，并且获得了可能的最小调节时间，响应的阶跃响应如图12所示。

设置开关频率为5khz，临界阻尼控制器增益作用下的实验结果如图13、图14所示，可见当参考电流给定突增时，实际并网电流没有发生震荡以及冲击现象，并且由图14所示q轴电流阶跃响应可知，实际电流在1ms以内即完全跟踪了给定信号，并且没有发生超调。

以上所述仅是本发明的优选实施方式，应当指出：对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。