基于多维全纯嵌入法的高维静态电压稳定边界计算方法与流程

本发明属于电力系统分析技术领域，具体涉及一种基于多维全纯嵌入法的高维静态电压稳定边界计算方法。

背景技术：

如何快速准确地计算电力系统高维静态电压稳定边界对于评估电力系统电压稳定性具有重要意义。

传统的连续潮流法在各个方向上不断地采用迭代型预测-修正策略来求解高维静态电压稳定边界，但此类方法在面对大型电力系统时会产生巨大的计算负担，难以实现在线应用。后来，提出了如切曲面法，轨道法等技术，但此类技术只用到了高维静态电压稳定边界上有限个点的信息，导致其准确性难以保证。此外，基于加勒金法的参数多项式方法可全局地逼近高维静态电压稳定边界，具有一定的探索价值。但总的来说，上述所有方法在求解电力系统潮流方程时大多采用传统迭代型潮流求解算法，如牛顿-拉夫逊法等，而牛顿-拉夫逊法在一定程度上存在发散问题或产生不可运行解的情况，这会间接影响上述方法结果的可靠性。

作为一种非迭代型潮流求解算法，全纯嵌入法在嵌入形式适当时可以保证求得电力系统的可运行电压解。因此，往往结合全纯嵌入法和帕德近似解析延拓技术来求解某一方向上的静态电压稳定边界，但此类方法无法直接计算出高维静态电压稳定边界且在面临大型电力系统时往往费时。总的来说，现有技术方法难以快速准确地求解电力系统的高维静态电压稳定边界。

技术实现要素：

本发明的目的在于，提供一种基于多维全纯嵌入法的高维静态电压稳定边界计算方法，快速准确地求得电力系统的高维静态电压稳定边界。

本发明提供一种基于多维全纯嵌入法的高维静态电压稳定边界计算方法，其特征在于，包括以下步骤：

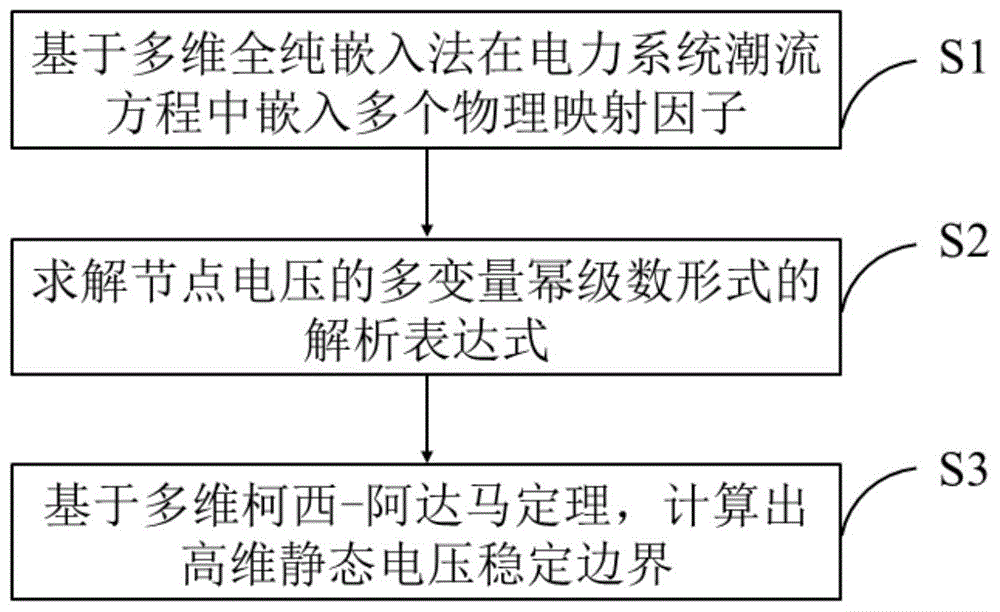
s1、基于多维全纯嵌入法在电力系统潮流方程中嵌入多个物理映射因子；

s2、求解节点电压的多变量幂级数形式的解析表达式；

s3、基于多维柯西-阿达马定理，计算出高维静态电压稳定边界。

进一步地，步骤s1具体包括：

s11、写出复数形式的电力系统潮流方程；

s12、基于多维全纯嵌入法，在潮流方程中嵌入多个物理映射因子。

进一步地，步骤s11中复数形式的电力系统潮流方程为：

式中，yik表示节点导纳矩阵中第i行第k列的元素，yik^*表示yik的共轭，pi和si分别表示节点i的有功功率注入和复功率注入，vi表示节点i的电压，vi^*表示vi的共轭，vk表示节点i的相邻节点k的电压，vk^*表示vk的共轭，vsw表示平衡节点的电压，|vi^sp|表示pv节点i电压的特定幅值，n表示电力系统的节点总数。

进一步地，步骤s12具体为：

基于多维全纯嵌入法，在潮流方程中嵌入多个物理映射因子s1,s2,…,s2d，得到含多个物理映射因子的潮流方程，含多个物理映射因子的潮流方程如下：

式中，2d表示2d个不同的维度，s1,s2,…,s2d表示2d个全纯物理映射因子，qi表示节点i的无功功率注入量，vi(s1,s2,…,s2d)和qi(s1,s2,…,s2d)分别表示多变量幂级数形式的节点i处的电压和无功功率全纯函数：

式中，vi[n1,n2,…,n2d]和qi[n1,n2,…,n2d]分别表示节点i的电压多变量幂级数和无功功率多变量幂级数的系数。

进一步地，步骤s2具体包括：

s21、计算含多个物理映射因子的潮流方程的初始解；

s22、建立节点电压多变量幂级数系数之间的递归关系；

s23、求解节点电压多变量幂级数形式的解析表达式。

进一步地，步骤s21具体为：

将s1＝0,s2＝0,…,s2d＝0代入含多个物理映射因子的潮流方程中：

计算出节点电压多变量幂级数系数的初始解，即第0阶系数vi[0,0,…,0]。

进一步地，步骤s22具体为：

使含多个物理映射因子的潮流方程两侧得同阶s1s2…s2d的系数一一对应相等，建立节点电压多变量幂级数的当前阶系数和之前阶系数的递归关系。

进一步地，步骤s23具体为：

根据节点电压多变量幂级数的当前阶系数和之前阶系数的递归关系，代入节点电压多变量幂级数系数的初始解，通过递归关系求得节点电压多变量幂级数的所有系数，进而得到节点电压多变量幂级数形式的解析表达式：

进一步地，步骤s3具体包括为：

s31、运用多维柯西-阿达马定理处理节点电压多变量幂级数表达式；

s32、计算出电力系统高维静态电压稳定边界。

进一步地，步骤s3具体为：

由多维柯西-阿达马定理可知，多变量幂级数形式的全纯函数的收敛域{sr1,sr2,…,sr2d}可由下式确定：

式中，vi[n1,n2…,n2d]表示节点电压多变量幂级数的系数，sr1,sr2,…,sr2d表示节点电压多变量幂级数在各个方向上的收敛半径；

基于多维柯西-阿达马定理，推导出高维静态电压稳定边界与节点电压多变量幂级数的前后项比例之间的解析关系：

式中，和分别表示节点电压多变量幂级数的第n阶和第(n+1)阶系数，sr1,sr2,…,sr2d为节点电压多变量幂级数在各个方向上的收敛半径，共同构成电力系统高维静态电压稳定边界。

本发明的有益效果是：本发明的基于多维全纯嵌入法的高维静态电压稳定边界计算方法采用含多个物理映射因子的多维全纯嵌入法求解潮流方程，可得节点电压的多变量幂级数形式的解析表达式；根据多维柯西-阿达马定理推导出的高维静态电压稳定边界与节点电压多变量幂级数的前后项比例之间的解析关系，能够快速准确地计算电力系统的高维静态电压稳定边界。

附图说明

图1是本发明实施例提供的一种基于多维全纯嵌入法的高维静态电压稳定边界计算方法的流程示意图；

图2是本发明实施例提供的一种表示含m个pq(负荷)节点，p个pv(发电机)节点和1个平衡节点的电力系统的示意图；

图3是本发明实施例提供的一种ieee39节点标准电力系统的网络结构示意图；

图4是本发明实施例提供的一种ieee39节点标准电力系统的区域划分示意图；

图5是本发明实施例提供的通过多维全纯嵌入法求得的ieee39节点标准电力系统的节点7电压示意图；

图6是本发明实施例提供的一种ieee39节点标准电力系统的高维静态电压稳定边界示意图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。此外，下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。

本发明的目的是解决现有方法所存在的难以快速准确计算电力系统高维静态电压稳定边界的技术问题：通过在电力系统潮流方程中嵌入多个物理映射因子，求得节点电压的多变量幂级数形式的解析表达式，之后根据多维柯西-阿达马定理推导出高维静态电压稳定边界与节点电压多变量幂级数的前后项比例之间的解析关系，从而快速准确地计算电力系统高维静态电压稳定边界。

图1是本发明实施例提供的一种基于多维全纯嵌入法的高维静态电压稳定边界计算方法的流程示意图，包括以下步骤：

s1、基于多维全纯嵌入法在电力系统潮流方程中嵌入多个物理映射因子；

在本发明实施例中，步骤s1可以通过以下方式实现：

图2表示含m个负荷pq节点，p个发电机pv节点和1个平衡节点的电力系统，其潮流方程为：

其中，yik是节点导纳矩阵中第i行第k列的元素，yik^*表示yik的共轭，pi和si表示节点i的有功功率注入和复功率注入，vi是节点i的电压，vi^*表示vi的共轭，vk为节点i的相邻节点k的电压，vk^*表示vk的共轭，vsw为平衡节点的电压，|vi^sp|代表pv(发电机)节点i电压的特定幅值，n为电力系统的节点总数。

接着，在公式(1)中嵌入多个物理映射因子s1,s2,…,s2d，得到含多个物理映射因子的电力系统潮流方程：

其中，2d表示2d个不同的维度，s1,s2,…,s2d表示2d个全纯物理映射因子，可分别用来独立调整电力系统不同节点的负荷或发电功率，yik是节点导纳矩阵中第i行第k列的元素，pi和si表示节点i的有功功率注入和复功率注入，qi表示节点i的无功功率注入量，vi是节点i的电压，vi^*表示vi的共轭，vk为节点i的相邻节点k的电压，vk^*表示vk的共轭，vsw为平衡节点的电压，|vi^sp|代表pv(发电机)节点i电压的特定幅值，n为电力系统的节点总数，vi(s1,s2,…,s2d)和qi(s1,s2,…,s2d)分别为多变量幂级数形式的节点i处的电压和无功功率全纯函数，即：

其中，s1,s2,…,s2d表示2d个全纯物理映射因子，可分别用来独立调整电力系统不同节点的负荷或发电功率，vi[n1,n2,…,n2d]和qi[n1,n2,…,n2d]分别为节点i的电压多变量幂级数和无功功率多变量幂级数的系数。

经过步骤s1，可得到含多个物理映射因子的电力系统潮流方程。

s2、求解节点电压的多变量幂级数形式的解析表达式；

在本发明实施例中，步骤s2可以通过以下方式实现：

将s1＝0,s2＝0,…,s2d＝0代入含多个物理映射因子的潮流方程(2)中：

根据公式(4)计算出节点电压多变量幂级数系数的初始解，即第0阶系数

然后，将含多个物理映射因子的潮流方程两侧同阶s1s2…s2d的系数一一对应相等，可建立节点电压多变量幂级数的当前阶系数(未知量)和之前阶系数(已知量)的递归关系。根据节点电压多变量幂级数的当前阶系数和之前阶系数的递归关系，代入节点电压多变量幂级数系数的初始解(即第0阶系数)，即可通过递归关系求得节点电压多变量幂级数的所有系数，从而得到节点电压多变量幂级数形式的解析表达式，即：

经过步骤s2，可得到电力系统节点电压多变量幂级数形式的解析表达式。

s3、基于多维柯西-阿达马定理，快速准确地计算出高维静态电压稳定边界；

在本发明实施例中，步骤s3可以通过以下方式实现：

由多维柯西-阿达马定理可知，多变量幂级数形式的全纯函数的收敛域{sr1,sr2,…,sr2d}可由下式确定：

其中，vi[n1,n2…,n2d]为节点电压多变量幂级数的系数，sr1,sr2,…,sr2d为节点电压多变量幂级数在各个方向上的收敛半径。

接下来推导高维静态电压稳定边界与节点电压多变量幂级数的前后项比例之间的解析关系。

首先，定义节点电压多变量幂级数前后项比例的上界为l：

其中，sup表示当n趋于无穷大时的上界，l是一个有限量，和分别表示节点电压多变量幂级数的第n阶和第(n+1)阶系数。

接着，给定一个任意小的正数ξ>0，则存在n使得下式满足：

那么类似公式(8)，从第m阶项到第n阶项满足公式(9)：

其中，m<n。将公式(9)相乘可得：

整理可得：

由于ξ是一个任意小的正数，于是对公式(11)两侧取极限并结合公式(7)可得：

类似公式(7)至公式(12)的推导过程，对于节点电压多变量幂级数前后项比例的下限，可得：

其中，inf表示当n趋于无穷大时的下界。

结合公式(12)和公式(13)可得：

因此，如果节点电压多变量幂级数前后项比例的极限存在，即公式(15)满足：

那么由公式(14)和公式(15)可得：

结合公式(6)，可得：

其中，和分别表示节点电压多变量幂级数的第n阶和第(n+1)阶系数，sr1,sr2,…,sr2d为节点电压多变量幂级数在各个方向上的收敛半径，共同构成电力系统高维静态电压稳定边界。

经过步骤s3，可以快速准确地计算出电力系统高维静态电压稳定边界。

下面通过在图3所示的ieee39节点标准电力系统中的实施例，并结合附图，对本发明的技术方案作进一步具体的说明。

首先，将图3所示的ieee39节点标准电力系统按照几何位置划分为3个区域，如图4所示。然后，根据上述步骤s1中介绍的多维全纯嵌入法，在电力系统潮流方程中嵌入3个物理映射因子s1,s2，s3，分别用于调整区域1、区域2和区域3内的电力系统运行状态，即负荷和发电功率。

接着，根据上述步骤s2中介绍的递归关系求解节点电压的多变量幂级数形式的解析表达式其中，s1,s2，s3为3个独立的物理映射因子，分别用于调整区域1、区域2和区域3内的电力系统运行状态，即负荷和发电功率，vi[n1,n2,n3]表示节点电压多变量幂级数系数。由步骤2所得的节点7的电压如图5所示，其中s3＝1。

最后，基于上述步骤s3中引用的多维柯西-阿达马定理，推导出电力系统高维静态电压稳定边界的解析表达式其中，和分别表示节点电压多变量幂级数的第n阶和第(n+1)阶系数，sr1,sr2,sr3为节点电压多变量幂级数在各个方向上的收敛半径，共同构成电力系统高维静态电压稳定边界。由步骤3所得高维静态电压稳定边界如图6所示，其中s3＝1，静态电压稳定的参考边界取自图5。由图6可知，随着节点电压多变量幂级数的阶数上升，所计算出的静态电压稳定边界越来越趋近参考边界，且在n＝9时就已非常切合参考边界了，即节点电压多变量幂级数的10次项比上9次项。此实施例证明了通过所提出的方法，仅需要节点电压多变量幂级数的前面少数几项，即可快速准确地计算出电力系统的高维静态电压稳定边界。

需要指出，根据实施的需要，可将本申请中描述的各个步骤/部件拆分为更多步骤/部件，也可将两个或多个步骤/部件或者步骤/部件的部分操作组合成新的步骤/部件，以实现本发明的目的。

尽管本发明较多地使用了电力系统、多维全纯嵌入法、潮流方程、多变量幂级数、高维静态电压稳定边界、解析表达式等术语，但并不排除使用其它术语的可能性。使用这些术语仅仅是为了更方便地描述和解释本发明的本质；把它们解释成任何一种附加的限制都是与本发明精神相违背的。

本领域的技术人员容易理解，以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。