一种基于光学计算的稀疏解混方法与流程

本发明涉及一种高光谱解混技术，特别涉及一种基于光学计算的新型稀疏解混方法。

背景技术：

由于实测对象的类型多样性、地物随时间实时变化以及地物光谱多次散射等问题存在，高光谱传感器在采样过程中不可避免的存在混合像元的情况。在高光谱图像分类研究中，如何获取亚像元精度上的真实属性信息，提高光谱影像分类精度，尤其是在系统实时性要求高，存在海量遥感数据以及对重构图像质量高保真要求的前提下，具有重要的学术价值而实际应用于亚像元目标探测、精细岩矿识别、对地伪装识别等领域具有非常现实的研究意义。

传统的混元解混算法有很多：光谱信号匹配，光谱角映射以及单形体体积法等。但是都有一个重要的假设前提条件：光谱库中端元数目大于或等于实测构成混合像元的端元数。但在实际生产生活中实测端元样本越来越多，使得端元光谱库规模日益扩大，往往出现端元数目远大于实测解混端元数的情况，使得大量端元构成表现出冗余特性。进一步传统解混算法采用先高速采样，后选取重要信息的小部分系数，再对这部分系数及其位置信息进行编码后，最后实施传输或存储的方式，使得传统方法存在成本昂贵，数据存储，传输效率以及有效信息获取困难等诸多问题。

为了解决该问题，最近几年有人提出将利用压缩感知(Compressive Sensing or Compressed Sensing,CS)理论中信号的稀疏特性来处理混合光谱稀疏解混所面对的预处理、端元提取以及多端元稀疏分解识别等问题。但是基于压缩感知理论的高光谱稀疏解混所涉及的信号稀疏化、测量值的获取以及丰度矩阵重构的高计算复杂度严重制约了该方法的进一步发展与实际应用。研究具有更准确提取实测端元、高保真端元精度、更加快速的提取速度为基础的高光谱稀疏解混新理论与新算法成为亟需解决的问题。

缺点：当前的高光谱稀疏解混技术，由于在处理过程中的高计算复杂度问题，存在着难以实时端元解混和丰度矩阵重建等问题。

因此亟需一种能实时、快速端元解混并精确重构丰度矩阵的方法。

技术实现要素：

有鉴于此，本发明的目的在于提供一种能实时端元解混并精确重构丰度矩阵的方法。

本发明的目的是通过以下技术方案来实现的，一种基于光学计算的稀疏解混方法，包括以下步骤：

S1：采用光学滤波方法获取高光谱信号的变换域稀疏系数矩阵；

S2：设计确定性测量矩阵实现高光谱信号的感知测量；

S3：通过硬件FPGA进行稀疏系数矩阵和确定性测量矩阵的并行乘法计算获取端元信号；

S4：利用高光谱信号的稀疏化结构信息以及结构化重构算法重构丰度矩阵。

进一步，所述步骤S1中，采用光学滤波方法获取高光谱信号的变换域稀疏系数矩阵包括光学非自适应多尺度变换步骤，具体包括以下子步骤：

S11：对高光谱信号进行多尺度分解，得到各带通子带；

S12：对各带通子带进行方向分解，得到空间滤波结果。

进一步，所述步骤S3中的并行计算获取端元信号，具体过程包括以下子步骤：

S31：把构造和优化的确定性测量矩阵预先放入可编程门阵列的ROM中；

S32：分块处理稀疏系数矩阵，并串行输入并存储在RAM中；

S33：根据步骤S32和步骤S33运用并行乘法计算实现高光谱信号的实时端元提取。

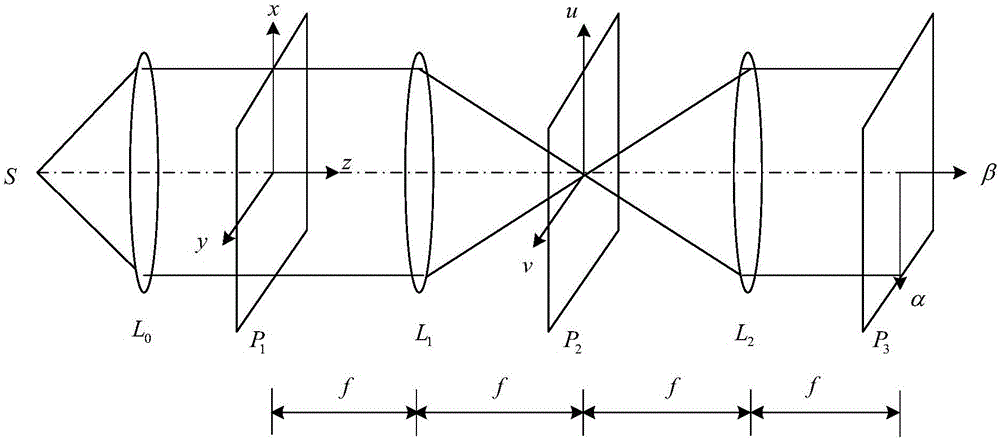
进一步，所述光学滤波方法包括匹配滤波方法，具体步骤描述如下：相干点光源S经准直透镜L₀形成轴向平行光，将输入某波段高光谱信号f(x,y)置于输入面P₁，经透镜L₁的光学傅里叶变换后，在其后的频谱面上将产生其频谱F(u,v)；在频谱面P₂上放置频域形式的滤波器ψ(x,y)的谱的共轭ψ^*(u,v)，相乘得到F(u,v)*ψ^*(u,v)；经过透镜L₂的傅里叶变换，在输出面P₃得到高光谱信号的空域滤波结果，即输入高光谱信号的光学非自适应多尺度变换其中，f为透镜焦距；为卷积。

进一步，所述光学滤波方法包括联合变换相关法，具体步骤描述如下：将激光1光束经过第一透镜7扩束准直后，通过分光镜2一部分光作为入射光照射在第一空间光调制器4上，在其对称光轴上分别放置输入图像3和空域形式的滤波器13，第一空间光调制器位于第二透镜5的前焦点处，经过傅里叶透镜的变换，利用第一CCD6采集其联合变换功率谱；然后，通过计算机将联合变换功率谱加载到第一空间光调制器上；另一部分光经反光镜8照射在第二空间光调制器9上，经过第三透镜10反变换作用，在第三透镜的后焦面处得到输出14，利用第二CCD11采集得到输入高光谱信号的空域滤波结果。

由于采用以上技术方案，本发明具有以下优点：

本发明采用光学滤波技术和电学系统实现多尺度几何分析，在保证重构精度的前提下大幅度的提高稀疏解混的效率，实现快速有效的稀疏分解。利用光子极高的信息容量和效率、极快的响应能力、极强的互连能力与并行能力，以及极大的存储能力等特点，将光子作为信息载体进行信息的存储、传输和处理，能更快速、精确地性重构丰度矩阵。因此，高光谱稀疏解混过程能够实现实时处理。

附图说明

为了使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明作进一步的详细描述，其中：

图1为基于光学计算的高光谱稀疏解混流程图；

图2为匹配滤波方法的光学4f系统；

图3为联合变换相关器。

具体实施方式

下面将结合附图，对本发明的优选实施例进行详细的描述。

图1为基于光学计算的高光谱稀疏解混流程图，图2为光学4f系统，图3为联合变换相关器。如图1所示：本发明提供的一种基于光学计算的高光谱稀疏解混方法，包括以下步骤：

第一步：采用光学滤波方法获取高光谱信号的变换域稀疏系数矩阵；

采用光学滤波方法获取高光谱信号的变换域稀疏系数矩阵包括光学多尺度变换步骤，光学多尺度变换包括：

1)光学非自适应多尺度变换(以轮廓波为代表)，具体包括以下子步骤：

S11：利用光学系统以及塔式滤波器组的特点实现高光谱信号的多尺度分解，得到各带通子带；

S12：利用光学技术和方向滤波器组对各带通子带进行方向分解，得到空间滤波结果。

2)光学自适应多尺度变换(以条带波为代表)，具体包括以下子步骤：

S11：利用现有的光学小波变换方法实现多尺度分解；

S12：通过电学数值计算完成最优四叉树的剖分；

S13：通过光学系统方法寻找一个最优方向；

S14：利用电学数值计算和最优方向得到光学自适应变换的结果。

在本发明中，采用光学非自适应多尺度变换。

在本发明中，所述光学滤波方法包括匹配滤波方法，具体步骤描述如下：相干点光源S经准直透镜L₀形成轴向平行光，将输入某波段高光谱信号f(x,y)置于输入面P₁，经透镜L₁的光学傅里叶变换后，在其后的频谱面上将产生其频谱F(u,v)；在频谱面P₂上放置频域形式的滤波器ψ(x,y)的谱的共轭ψ^*(u,v)，相乘得到F(u,v)*ψ^*(u,v)；经过透镜L₂的傅里叶变换，在输出面P₃得到高光谱信号的空域滤波结果，即输入高光谱信号的光学非自适应多尺度变换其中，f为透镜焦距；为卷积。

所述光学滤波方法包括联合变换相关法，具体步骤描述如下：将激光1光束经过第一透镜7扩束准直后，通过分光镜2一部分光作为入射光照射在第一空间光调制器4上，在其对称光轴上分别放置输入图像3和空域形式的滤波器13，第一空间光调制器位于第二透镜5的前焦点处，经过傅里叶透镜的变换，利用第一CCD6采集其联合变换功率谱；然后，通过计算机将联合变换功率谱加载到第一空间光调制器上；另一部分光经反光镜8照射在第二空间光调制器9上，经过第三透镜10反变换作用，在第三透镜的后焦面处得到输出14，利用第二CCD11采集得到输入高光谱信号的空域滤波结果。

第二步：设计Toeplitz确定性测量矩阵实现高光谱信号的感知测量；

第三步：通过硬件FPGA进行稀疏系数矩阵和测量矩阵的并行乘法计算获取端元信号；所述第三步中的并行乘法计算来获得端元信号，具体过程如下：

S31：把构造的Toeplitz确定性测量矩阵预先放入可编程门阵列的ROM中；

S32：分块处理稀疏系数矩阵，并串行输入并存储在RAM中；

S33：根据步骤S32和步骤S33运用并行乘法计算实现高光谱信号的实时端元提取。

第四步：利用高光谱信号的稀疏化结构信息以及实时提取的端元，结合压缩感知理论中RtOMP结构化重构算法，重构出该端元对应的丰度矩阵，从而实现丰度矩阵稀疏解混的目的。

本发明将光学滤波方法应用于高光谱稀疏解混中，结合光学计算和压缩感知理论，采用硬件FPGA和并行乘法计算实现测量矩阵和稀疏矩阵的并行处理，运用结构化重构算法实现高光谱信号的实时丰度矩阵重建。

最后说明的是，以上优选实施例仅用以说明本发明的技术方案而非限制，尽管通过上述优选实施例已经对本发明进行了详细的描述，但本领域技术人员应当理解，可以在形式上和细节上对其作出各种各样的改变，而不偏离本发明权利要求书所限定的范围。