基于幂指数可调的攻击成本下复杂网络边攻击方法与流程

本发明涉及到复杂网络鲁棒性方面，具体是一种在幂指数可调的攻击成本下研究不同边攻击策略对复杂网络的攻击方法。

背景技术：

互联网、军事网、交通网、电力网等网络为人们生活带来极大的便利，但同时也存在着一系列的安全性问题.一些重要网络遭受攻击或者陷入瘫痪会使整个国家陷入混乱。为了优化网络结构以增强网络的抗攻击性，对复杂网络攻击策略进行深入的研究愈发重要。

当前，复杂网络边攻击策略的研究主要基于无成本前提假设，无成本是指移除网络中节点或边时不考虑攻击成本，然而不同规模的网络性质不同攻击成本也不一样。前人的研究对于节点做了考虑攻击成本时的攻击，并指出成本下对复杂网络的研究更接近现实网络.成本下是指移除网络中节点或边时需要考虑攻击成本，虽然成本下研究攻击策略更真实，但是对于边的攻击并没有加入攻击成本的研究。

技术实现要素：

本发明针对现有复杂网络边攻击策略存在的问题，提出一种基于幂指数可调的攻击成本下复杂网络边攻击方法。

本发明采用的技术方案是：基于幂指数可调的攻击成本下复杂网络边攻击方法，所述方法包括如下步骤:

第一步:首先生成一定规模的复杂网络；

第二步:求出各条边的权重；

第三步:利用边权重得到边攻击策略；

第四步:开始攻击并在攻击过程中加入攻击成本因素；

第五步:得出网络规模与成本的关系。

所述的基于幂指数可调的攻击成本下复杂网络边攻击方法，其具体步骤如下:

第一步:首先生成一定规模的BA无标度网络，其模型的构造方法:

(1)增长：开始于较少的节点数量m₀，在每个时间间隔增添一个具有m条边的新节点，其中m≤m₀，连接这个新节点到m个不同的已经存在于系统中的节点上；

(2)择优连接：在选择新节点的连接点时，假设新节点连接到节点i的概率Π_i取决于节点i的度数k_i和节点j的度数k_j,即其中,j为网络已存在的节点总数。

在经过t步后，产生一个包含N＝t+m₀个节点和mt条边的网络；

第二步:根据生成的网络的节点的度按照边权重的表示方法求出两节点之间所连边的权重；

第三步:按照边攻击策略中的边权排序方式分别对边进行排序，排序完再分别使用相关策略攻击生成的网络边；

第四步:将被攻击边的权重添加到移除边的权重总和中，按照总攻击成本的公式再重新计算总攻击成本ρ的值,如果ρ的值没有比所给成本值大，那么这条边被直接移除，继续迭代直到ρ的值达到所给的成本值；

第五步:计算最大连通子图的相对大小G；

经过上述步骤，可以得到不同边攻击策略下最大连通子图G与幂指数θ的关系曲线图以及最大连通子图G与总攻击成本ρ的关系曲线图；通过观察曲线图中参数之间的变化关系可以得出对于采用什么攻击策略来攻击已知拓扑结构的网络具有重要指导意义。

所述边权重的表示方法：

一个具体的网络可抽象为一个由点集V和边集E组成的图G＝(V,E)，顶点数记为N＝|V|,边数记为M＝|E|；一般使用权重邻接矩阵W＝(w_ij)_n×n,表示加权网络权重，w_ij表示节点v_i和节点v_j连接的边的权重，当网络中各条边的权值都相同时，加权网络即退化为无权网络；边权与两个节点的度相关，边权重可以定义为:假设网络的边e_ij连接的两个节点v_i和v_j的度值分别是k_i和k_j,那么这条边的权重为w_ij＝w_ji＝(k_i*k_j)^θ，其中θ>0是一个可调的权重参数，用于描述边权与节点度之间的相互关系。

所述的基于幂指数可调的攻击成本下复杂网络边攻击方法，所述边的攻击策略采用3种攻击策略，即基于初始图面向边权重的重要性度量指标的攻击，这3种攻击策略分别为:

①将网络生成的边按照其权重大小随机排序，按照此排序结果对边进行攻击；

②将网络生成的边按照其权重由小到大的顺序进行排序，按照此排序结果对边进行攻击；

③将网络生成的边按照其权重由大到小的顺序进行排序，按照此排序结果对边进行攻击。

所述的基于幂指数可调的攻击成本下复杂网络边攻击方法，

所述总的攻击成本ρ定义为:

式中w_i是边i的权重，w_l是被移除的边的权重，Z是移除边的数量总和。

本发明对比已有技术具有以下创新点:

①对于复杂网络边攻击策略考虑了边攻击成本；

②边攻击成本带有可调幂指数。

与现有技术相比，本方法的优点在于:

①突破以往研究局限，不再拘泥于复杂网络无攻击成本或攻击成本都一样的研究思路；

②更加贴近实际网络面对攻击的情形，对于实际网络布局与优化具有重要指导意义。

附图说明

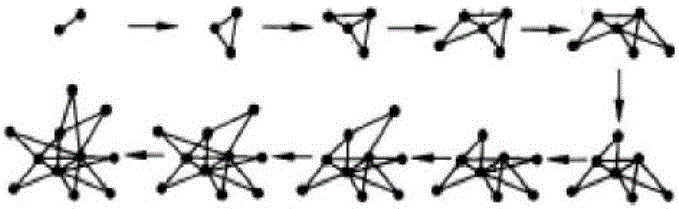
图1是本发明中所用到的生成网络模型示意图；

图2是本发明的攻击边前后模型示意图；

图3是本发明采用基于幂指数可调的攻击成本下复杂网络边攻击方法进行复杂网络鲁棒性分析的流程示意图。

具体实施方式

下面将对本发明作进一步的详细说明。

首先介绍如下的概念与定义:

1、BA无标度网络

无标度模型由Albert-LászlóBarabási和Réka Albert在1999年首先提出，现实网络的无标度特性源于众多网络所共有的两种生成机制：(i)网络通过增添新节点而连续扩张；(ii)新节点择优连接到具有大量连接的节点上。

此模型的构造方法:

(1)增长：开始于较少的节点数量m₀，在每个时间间隔增添一个具有m条边的新节点，其中m≤m₀，连接这个新节点到m个不同的已经存在于系统中的节点上。

(2)择优连接：在选择新节点的连接点时，假设新节点连接到节点i的概率Π_i取决于节点i的度数k_i和节点j的度数k_j,即其中,j为网络已存在的节点总数。

在经过t步后，产生一个包含N＝t+m₀个节点和mt条边的网络，图1显示了BA模型的初始值m＝m₀＝2时的网络演化过程，初始网络有两个节点，每次新增加一个节点按照优先连接机制与网络中已存在的两个节点相连接，详见说明书附图1。

2、边权重的定义

一个具体的网络可抽象为一个由点集V和边集E组成的图G＝(V,E)。顶点数记为N＝|V|,边数记为M＝|E|。一般使用权重邻接矩阵W＝(w_ij)_n×n,表示加权网络权重。w_ij表示节点v_i和节点v_j连接的边的权重，当网络中各条边的权值都相同时，加权网络即退化为无权网络。边权与两个节点的度相关，边权重可以定义为:假设网络的边e_ij连接的两个节点v_i和v_j的度值分别是k_i和k_j,那么这条边的权重为w_ij＝w_ji＝(k_i*k_j)^θ，其中θ>0是一个可调的权重参数，用于描述边权与节点度之间的相互关系。

3、边攻击策略

边攻击策略的定义都是基于边的重要性度量指标，如边的权重等，即将边按照其权重的大小进行排序并移除。攻击策略可以按照边的重要性度量指标攻击网络，本方法采用3中攻击策略，即基于初始图面向边权重的重要性度量指标的攻击。这3种攻击策略分别为:

①将网络生成的边按照其权重大小随机排序，按照此排序结果对边进行攻击。

②将网络生成的边按照其权重由小到大的顺序进行排序按照此排序结果对边进行攻击。

③将网络生成的边按照其权重由大到小的顺序进行排序，按照此排序结果对边进行攻击。

4、最大连通子图

本文采用最大连通子图相对值G来衡量网络的崩溃程度。G定义为最大连通子图的规模N'与原始网络规模N的比值，即G＝N'/N。式中N'表示相继故障结束后网络的最大连通子图包含的节点个数。N表示原始网络节点数。G的值越大，表示网络的鲁棒性越强。

5、攻击成本的定义

传统的复杂网络攻击性研究大多基于”无成本”条件，但是，不同网络节点和边的性质不同，攻击成本可能是不同的。本方法采用边的权重近似衡量攻击成本，即cost_i＝w_i。

总的攻击成本定义为:

式中w_i是边i的权重,w_l是被移除边的权重，Z是移除边的数量总和。

本发明提供的基于幂指数可调的攻击成本下复杂网络边攻击方法具体步骤如下，具体流程见说明书附图3:

第一步:首先生成一定规模的BA无标度网络，比如N＝5000,m＝m₀＝2。

第二步:根据生成的网络的节点的度按照定义2求出两节点之间所连边的权重。

第三步:按照上面定义3中提到的三种边攻击策略中的边权排序方式分别对边进行排序，排序完再分别使用相关策略攻击生成的网络边，攻击边前后模型示意图见说明书附图2，其中,a为攻击前网络的一条边，b和e是其相邻边；攻击后a边消失,b和e保持完好。

第四步:将被攻击边的权重添加到移除边的权重总和中，按照上述定义5中总攻击成本的公式再重新计算ρ的值,如果ρ的值没有比所给成本值大，那么这条边被直接移除，继续迭代直到ρ的值达到所给的成本值。

第五步:计算最大连通子图的相对大小G。

经过上述步骤，可以得到不同边攻击策略下最大连通子图G与幂指数θ的关系曲线图以及最大连通子图G与总攻击成本ρ的关系曲线图。通过观察曲线图中参数之间的变化关系可以看出在考虑成本时采用什么攻击策略来攻击已知拓扑结构的网络效果更具有破坏性。