混合云模式中的基于成本考虑的在线服务请求调度方法与流程

本发明涉及云服务技术领域，具体地，涉及混合云模式中的基于成本考虑的在线服务请求调度方法。

背景技术：

李雅普诺夫优化技术通常被用来求解时均意义上的优化量。在优化问题中，有一大类问题是与时间相关的，例如与工作负载相关的问题就是随着时间变化而不断变化的。因此时均意义上的优化可以更好地优化全局系统的状态。而带有时均变量的优化问题很难用通常的优化方法进行解决，李雅普诺夫优化技术就可以被用来解决这类问题。李雅普诺夫优化技术原本来源于自动控制领域中的李雅普诺夫稳定性。因此最初该技术也是用于进行动态队列网络中的最优控制。但由于改进技术的优秀性质，之后被拓展到其他领域用于解决求解时均量的优化问题。

由于服务请求的波动性，当服务请求突然增多时，企业或组织内部的私有云的资源是不够用的，如果购买硬件设施来处理这些随机的增多的服务请求，不仅成本高，而且大多数的时候这些硬件是处于闲置状态，严重浪费资源。由于混合云架构的特性，当私有云中的资源不够用的时候，可以以较低的价格租用公有云中的资源。因此越来越多的企业或组织将已有的基础设施作为自己的私有云，处理企业或组织内部的大部分服务任务，当服务请求突然增多，私有云资源不够用的时候，租用公有云中的资源以应对服务请求的爆炸式突增。用户的服务请求是实时随机到达的，其到达的波动性很大，规律很难预测，而且有些服务请求处于安全隐私的考虑希望被运行在私有云上，这样的服务请求一般都是处理公司里的重要事务的，因此企业是希望这种类型的服务请求的拒绝率不能太高，否则会影响公司的正常业务。这种情况下做一个基于成本考虑的最优的服务请求调度是很困难的。目前针对这个问题主要是考虑静态的情况，即知道服务请求到达的所有全局信息，这样的假设前提是不符合实际的。

由于私有云是企业固有的资产，运行在私有云上的服务请求是不需要花费租金的，所以我们假设运行在私有云上服务请求成本花销为零。为了使租用公有云的花销成本最小，我们可以将所有的服务请求都运行在私有云上，然而由于私有云的资源是有限的，如果所有的请求都调度在私有云上，那么当私有云中的资源不够用的时候，对于那些只能运行在私有云上的服务请求就会被拒绝，如果被拒绝的这类请求太多，就会影响公司的正常运营，因此如何使最小花费成本和拒绝率之间达到平衡是关键。

本发明为了在保证拒绝率的情况下，得到最少的花费的服务请求调度方法，提出了一个在混合云模式下的基于成本考虑的在线的服务请求调度策略，同时利用李雅普诺夫优化技术，将整个时间段上的平均优化目标转化为每个时间槽中的优化目标，这样通过解这个转化过后的优化问题我们可以实时的做出调度决策。

技术实现要素：

针对现有技术中的缺陷，本发明的目的是提供一种混合云模式中的基于成本考虑的在线服务请求调度方法。

根据本发明提供的混合云模式中的基于成本考虑的在线服务请求调度方法，包括如下步骤：

步骤1：构建以平均花销成本最小化为目标，私有云资源有限，服务拒绝率为限制条件的最优化问题；

步骤2：利用李雅普诺夫优化方法将步骤1中的最优化问题转化为单时槽中的优化问题；

步骤3：采用最优衰减算法求解步骤2中单时槽中的优化问题的最优解，即得到当前时刻的服务请求的调度方法。

优选地，所述步骤1中的最优化问题如下：

subject to:

Y_it,Z_jt∈{0,1} (2)

式中：Y_it,Z_jt是取0,1的决策变量，Y_it表示t时刻只能运行在私有云上的第i个请求，n_t表示t时刻此类请求的总量；Z_jt表示t时刻可以运行在私有云或公有云上的第j个请求，m_t表示t时刻此类请求的总量；a_ivt,b_jvt分别表示t时刻只能运行在私有云上的第i个请求对第v种类型的虚机的请求数量以及表示t时刻运行在私有云或公有云上的第j个请求对第v种类型的虚机的请求数量；c_v代表v类型虚拟机的单位时间价格；t_j表示第j个请求的服务时间；v_vk代表v类型的虚拟机中k资源的数量；k取1,2,3分别表示资源类型为CPU，memory，storage disk；T表示整个时间槽数量；h表示虚机类型的数量，T_kt表示t时刻k类型资源的总量，α表示拒绝率的阈限；公式(3)限定了t时刻所请求的资源数量不能大于t时刻私有云中空余的资源量；公式(4)限定了平均拒绝率低于阈限值α。

优选地，所述步骤2包括：

步骤2.1：构造虚拟队列H来记录被拒绝的服务请求数量，计算公式如下：

H(0)＝0

式中：H(t+1)表示t+1时刻被拒绝的服务请求数量，H(t)表示t时刻被拒绝的服务请求数量，H(0)表示0时刻被拒绝的服务请求数量为0；

步骤2.2：构造李雅普诺夫函数及李雅普诺夫偏移，计算公式如下：

Δ(L(H(t)))＝E{L(H(t+1))-L(H(t))|H(t)}

式中：L(H(t))表示H(t)的李雅普诺夫函数，Δ表示李雅普诺夫偏移运算，L(H(t+1))表示H(t+1)的李雅普诺夫函数；

步骤2.3：求出李雅普诺夫偏移的上限，计算公式如下：

式中：n_t表示t时刻只能运行在私有云上请求的总量，E[.|.]表示在H(t)条下的的期望运算；

步骤2.4：构造单时槽优化问题的目标函数，函数如下：

式中：V表示调节参数，用于控制花销成本和服务拒绝的数量之间的偏重，重新构建单时槽的优化问题如下：

subject to：

Y_it,Z_jt∈{0,1}

优选地，所述步骤3中的最优衰减算法包括如下步骤：

步骤A1：获取t时刻所有的请求以及衰减序列d，d是目标函数中的决策变量系数的绝对值从小到大的序列；

步骤A2：获取不考虑所有限制条件时，单时槽优化问题的目标函数的最优解，记为op；

步骤A3：判断op所需的资源量是否小于公有云当前时刻的空余量，若op所需的资源量小于公有云当前时刻的空余量，则执行步骤A4；若op所需的资源量大于等于公有云当前时刻的空余量，则执行步骤A5；

步骤A4：将步骤A3得到的op作为最优解，更新剩余资源量T，令T的值为前一时刻的T的值减去N(Rt)后得到的值，N(Rt)表示t时刻决策所消耗的资源量，结束流程；

步骤A5：根据衰减序列d衰减单时槽优化问题的目标函数后得到新的op值，返回执行步骤A3。

与现有技术相比，本发明具有如下的有益效果：

本发明中的方法能够针对未知的在线服务请求，即针对不知道任意将来时刻的服务请求到达的规律，使得整个时间区域内的平均租用公有云的花费成本达到最低，以服务请求拒绝率及私有云资源为限制条件的优化问题；然后利用李雅普诺夫优化技术将原问题转化为不含时均量的优化问题，从而实现花销成本和服务拒绝率之间的有效权衡。

附图说明

通过阅读参照以下附图对非限制性实施例所作的详细描述，本发明的其它特征、目的和优点将会变得更明显：

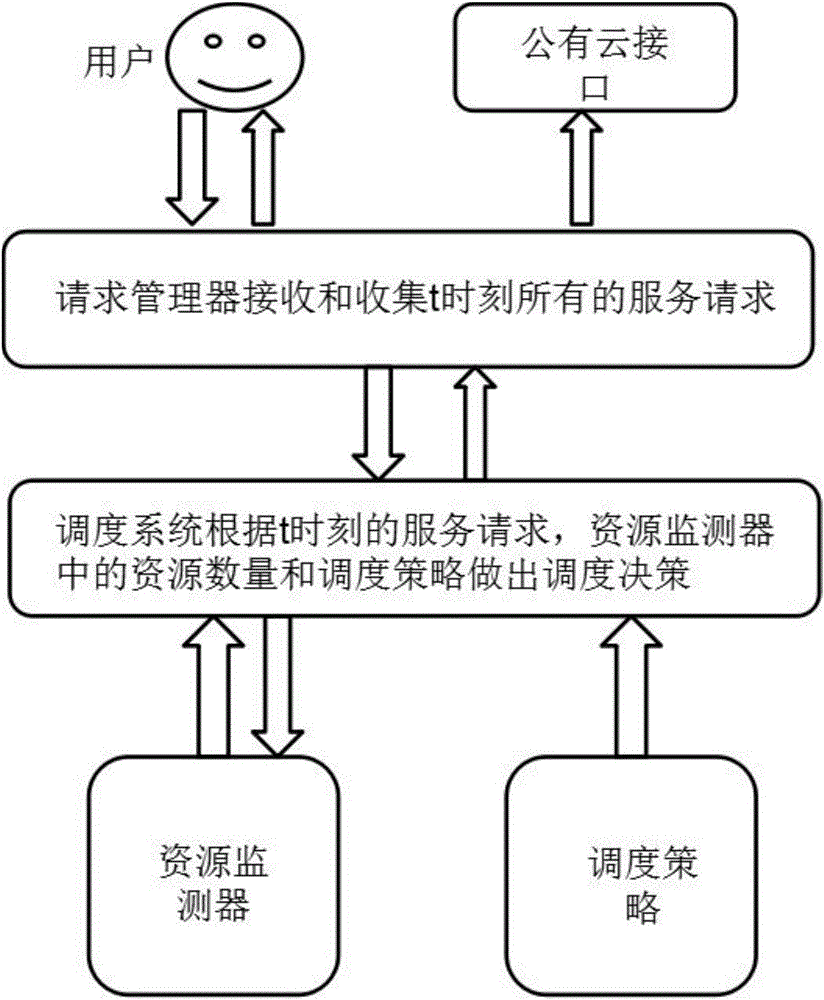
图1为混合云中服务请求调度的基本框架图；

图2为基于框架的服务请求调度流程图；

图3为最优衰减算法流程图。

具体实施方式

下面结合具体实施例对本发明进行详细说明。以下实施例将有助于本领域的技术人员进一步理解本发明，但不以任何形式限制本发明。应当指出的是，对本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变化和改进。这些都属于本发明的保护范围。

根据本发明提供的混合云模式中的基于成本考虑的在线服务请求调度方法，若假设知道全局的服务请求信息来对在线服务请求进行调度，这样的假设是不合理的。在本发明中针对不知道任意将来时刻的服务请求到达规律，提出了在线的服务请求调度策略，使得整个时间区域内的平均租用公有云的花费成本是最低的，服务请求拒绝率及私有云资源为限制条件的优化问题；然后利用李雅普诺夫优化技术，将原问题转化为不含时均量的优化问题，转化过后的问题是一个典型的0-1背包问题，为了提高求解这个问题的速度本发明中提出一种最优衰减算法求解这个问题。

由于服务请求的到达是随机的，且服务请求的虚拟机的种类，数量以及要求服务的时间都是随机的，因此难以预测这些具体的服务请求。因此，需要首先构建一个以平均花销成本最小化为目标，私有云资源有限，服务拒绝率为限制条件的最优化问题：

subject to:

Y_it,Z_jt∈{0,1} (2)

式中：Y_it,Z_jt是取0,1的决策变量，Y_it表示t时刻只能运行在私有云上的第i个请求，n_t表示t时刻此类请求的总量；Z_jt表示t时刻可以运行在私有云或公有云上的第j个请求，m_t表示t时刻此类请求的总量；a_ivt,b_jvt分别表示t时刻只能运行在私有云上的第i个请求对第v种类型的虚机的请求数量以及表示t时刻运行在私有云或公有云上的第j个请求对第v种类型的虚机的请求数量；c_v代表v类型虚拟机的单位时间价格；t_j表示第j个请求的服务时间；v_vk代表v类型的虚拟机中k资源的数量；k取1,2,3分别表示资源类型为CPU，memory，storage disk；T表示整个时间槽数量；h表示虚机类型的数量，T_kt表示t时刻k类型资源的总量，α表示拒绝率的阈限。公式(3)限定了t时刻所请求的资源数量不能大于t时刻私有云中空余的资源量；公式(4)限定了平均拒绝率低于阈限值α。

可以看到，该问题是一个0-1线性规划问题，但是这个问题的目标，及请求拒绝率的限制条件都是时均的，因此使用传统0-1线性规划方法很难解决这个问题。接下来就利用李雅普诺夫优化技术，将问题转化为单时槽中的优化问题来解决，具体解决方案如下：

步骤S1：首先构造虚拟队列H来记录被拒绝的服务请求数量：

H(0)＝0

式中：H(t+1)表示t+1时刻被拒绝的服务请求数量，H(t)表示t时刻被拒绝的服务请求数量，H(0)表示0时刻被拒绝的服务请求数量为0；

步骤S2：接下来构造李雅普诺夫函数及李雅普诺夫偏移：

Δ(L(H(t)))＝E{L(H(t+1))-L(H(t))|H(t)}

式中：L(H(t))表示H(t)的李雅普诺夫函数，Δ表示李雅普诺夫偏移运算，L(H(t+1))表示H(t+1)的李雅普诺夫函数；

步骤S3：求出李雅普诺夫偏移的上限：

式中：E[.|.]表示在H(t)条下的的期望运算；

步骤S4：构造单时槽优化问题的目标函数：

式中：V表示调节参数，用于控制花销成本和服务拒绝的数量之间的偏重。到这里，重新构建单时槽的优化问题如下：

subject to：

Y_it,Z_jt∈{0,1}

为了提高求解该问题的效率，本发明利用最优衰减算法求解该优化问题，从而能够得到当前时刻的服务请求的调度决策，从而取得成本花销和服务请求被拒绝数量之间的平衡。

图1位服务请求调度的四个基本组成模块：请求管理器，调度系统，资源检测器和公有云接口。图2展示了服务请求调度的基本流程。首先请求管理器接收和收集t时刻所有的服务请求，并将这些服务请求转发到调度系统；然后调度系统接收到这些服务请求，调用资源监测器中t时刻的资源剩余情况，根据请求调度策略做出调度决策，并将此刻的调度策略返回给请求管理器；请求管理器发布调度策略给私有云和公有云接口执行调度决策并将调度决策的结果返回给用户。

以上对本发明的具体实施例进行了描述。需要理解的是，本发明并不局限于上述特定实施方式，本领域技术人员可以在权利要求的范围内做出各种变化或修改，这并不影响本发明的实质内容。在不冲突的情况下，本申请的实施例和实施例中的特征可以任意相互组合。