基于d级cat态和d级Bell态纠缠交换的多方量子隐私比较方法与流程

本发明涉及量子密码学领域。本发明设计一种基于d级cat态和d级Bell态纠缠交换的多方量子隐私比较方法，解决多个用户秘密的相等性比较问题。

背景技术：

自从Bennett和Brassard[1]在1984年首次提出量子密码的概念，许多安全量子密码方法已经被设计出来，如量子秘钥分配(Quantum Key Distribution，QKD)[2-5]、量子安全直接通信(Quantum Secure Direct Communication，QSDC)[6-8]、量子隐形传态[9-11]等。

安全多方计算(Secure multi-party computation，SMC)，是现代密码学的一个基本的原始的问题，致力于在分布式网络计算一个带有不同方秘密输入的函数而不泄露每个秘密输入的真实内容。它在隐秘招标和拍卖、无记名投票选举、电子商务、数据挖掘等有着广泛的应用，在经典密码学中长期作为广泛研究的对象。然而，SMC的安全性是基于计算复杂性假设，是易受量子计算的强大能力影响的。在这种情形下，经典SMC被推广到量子力学领域，从而诞生了量子安全多方计算(Quantum secure multi-party computation，QSMC)。

首次被Yao[12]在百万富翁问题中提出的隐私比较，是SMC的一个基本问题。在百万富翁问题[12]中，两个百万富翁希望判断出谁更富有而不能知道彼此的真实财产。后来，Boudot等[13]提出一个方法来判决两个百万富翁是否同样富有。然而，Lo[14]指出，在两方情形下构建出一个安全的相等性函数是不可能的。因此，一些额外的假设，如一个第三方(Third party，TP)，应当被考虑以完成隐私比较任务。

量子隐私比较(Quantum private comparison，QPC)，可被视为经典隐私比较在量子力学领域的推广，是首次由Yang等[15]在2009年提出的。QPC的目标在于在它们的真实内容都没有被泄露出去的前提下通过利用量子力学原理判断来自不同方的秘密输入是否相等。自从那时起，许多QPC方法[16-38]已经被构建出来。

多方量子隐私比较(Multi-party quantum private comparison，MQPC)是一种想比较出她们秘密输入的相等性的参与方多于两方的QPC。假设存在n方，如果她们采用一个两方QPC方法来实现她们的秘密输入的相等性比较，她们将不得不执行(n-1)～n(n-1)/2次这个方法。这样，比较效率被降低了。一个问题自然而然地冒出来：来自n方的秘密输入的相等性比较能否通过只执行一次方法就完成？在2013年，Chang等[39]利用n粒子GHZ类态提出第一个MQPC方法来给这个问题一个肯定的答案，这个方法只被执行一次就能完成n方中任意对的相等性比较。自从那时起，MQPC已经吸引了越来越多的注意力。基于多级量子系统的MQPC方法[40，41]后来也被构建出来。

基于以上分析，本发明利用d级cat态和d级Bell态纠缠交换提出一种新颖的MQPC方法。本发明的方法只执行一次就能完成n方秘密的相等性比较。除了她们的秘密完全相同的情形，一方不能得到其他方的秘密。除了比较结果，半忠诚TP无法得到关于这些方的秘密的任何信息。

参考文献

[1]Bennett，C.H.，Brassard，G.：Quantum cryptography：Public-key distribution and coin tossing.Proc.IEEE Int.Conf.Computers，Systems and Signal Processing，1984，175-179

[2]Ekert，A.K.：Quantum cryptography based on Bell’s theorem.Phys Rev Lett，1991，67(6)：661-663

[3]Bennett，C.H.：Quantum cryptography using any two nonorthogonal states.Phys Rev Lett，1992，68(21)，3121

[4]Cabello，A.：Quantum key distribution in the Holevo limit.Phys Rev Lett，2000，85：5635

[5]Shih，H.C.，Lee，K.C.，Hwang，T.：New efficient three-party quantum key distribution protocols.IEEE J Sel Top Quantum Electron，2009，15(6)，1602-1606

[6]Long，G.L.，Liu，X.S.：Theoretically efficient high-capacity quantum-key-distribution scheme.Phys Rev A，2002，65：032302

[7]Bostrom，K.，Felbinger，T.：Deterministic secure direct communication using entanglement.Phys Rev Lett，2002，89：187902

[8]Chong，S.K.，Hwang，T.：The enhancement of three-party simultaneous quantum secure direct communication scheme with EPR pairs.Opt Commun，2011，284(1)：515-518

[9]Bouwmeester，D.，Pan，J.W.，Mattle，K.，Eibl，M.，Weinfurter，H.，Zeilinger，A.：Experimental quantum teleportation.Nature，1997，390(6660)：575-579

[10]Zhang，Z.J.，Liu，Y.M.，Man，Z.X.：Many-agent controlled teleportation of multi-qubit quantum information via quantum entanglement swapping.Commun Theor Phys，2005，44(5)：847-849

[11]Yin，X.F.，Liu，Y.M.，Zhang，Z.Y，Zhang，W.，Zhang，Z.J.：Perfect teleportation of an arbitrary three-qubit state with the highly entangled six-qubit genuine state.Sci China-Phys Mech Astron，2010，53(11)：2059-2063

[12]Yao，A.C.：Protocols for secure computations.In：Proceedings of 23rd IEEE Symposium on Foundations of Computer Science(FOCS’82)，Washington，DC，USA，1982，pp.160

[13]Boudot，F.，Schoenmakers，B.，Traor’e，J.：A fair and efficient solution to the socialist millionaires’problem.Discret Appl Math(Special Issue on Coding and Cryptology)，2001，111(1-2)：23-36

[14]Lo，H.K.：Insecurity of quantum secure computations.Phys Rev A，1997，56(2)：1154-1162

[15]Yang，Y.G.，Wen，Q.Y.：An efficient two-party quantum private comparison protocol with decoy photons and two-photon entanglement.J Phys A：Math Theor，2009，42：055305

[16]Chen，X.B.，Xu，G.，Niu，X.X.，Wen，Q.Y.，Yang，Y.X.：An efficient protocol for the private comparison of equal information based on the triplet entangled state and single-particle measurement.Opt Commun，2010，283：1561

[17]Lin，J.，Tseng，H.Y.，Hwang，T.：Intercept-resend attacks on Chen et al.’s quantum private comparison protocol and the improvements.Opt Commun，2011，284：2412-2414

[18]Yang，Y.G.，Gao，W.F.，Wen，Q.Y.：Secure quantum private comparison.Phys Scr，2009，80：065002

[19]Liu，W.，Wang，Y.B.，Cui，W.：Quantum private comparison protocol based on Bell entangled states.Commun Theor Phys，2012，57：583-588

[20]Yang，Y.G.，Xia，J.，Jia，X.，Shi，L.，Zhang，H.：New quantum private comparison protocol without entanglement.Int J Quantum Inf，2012，10：1250065

[21]Chen，X.B.，Su，Y.，Niu，X.X.，Yang，Y.X.：Efficient and feasible quantum private comparison of equality against the collective amplitude damping noise.Quantum Inf Process，2014，13：101-112

[22]Liu，B.，Gao，F.，Jia，H.Y.，Huang，W.，Zhang，W.W.，Wen，Q.Y.：Efficient quantum private comparison employing single photons and collective detection.Quantum Inf Process，2013，12：887-897

[23]Zi，W.，Guo，F.Z.，Luo，Y.，Cao，S.H.，Wen，Q.Y.：Quantum private comparison protocol with the random rotation.Int J Theor Phys，2013，52：3212-3219

[24]Tseng，H.Y.，Lin，J.，Hwang，T.：New quantum private comparison protocol using EPR pairs.Quantum Inf Process，2012，11：373-384

[25]Wang，C.，Xu，G.，Yang，Y.X.：Cryptanalysis and improvements for the quantum private comparison protocol using EPR pairs.Int.J.Quantum Inf，2013，11：1350039

[26]Yang，Y.G.，Xia，J.，Jia，X.，Zhang，H.：Comment on quantum private comparison protocols with a semi-honest third party.Quantum Inf Process，2013，12：877-885

[27]Zhang，W.W.，Zhang，K.J.：Cryptanalysis and improvement of the quantum private comparison protocol with semi-honest third party.Quantum Inf Process，2013，12：1981-1990

[28]Li，Y.B.，Ma，Y.J.，Xu，S.W.，Huang，W.，Zhang，Y.S.：Quantum private comparison based on phase encoding of single photons.Int J Theor Phys， 2014，53：3191-3200

[29]Liu，X.T.，Zhang，B.，Wang，J.，Tang，C.J.，Zhao，J.J.：Differential phase shift quantum private comparison.Quantum Inf Process，2014，13：71-84

[30]Liu，W.，Wang，Y.B.：Quantum private comparison based on GHZ entangled states.Int J Theor Phys，2012，51：3596-3604

[31]Li，J.，Zhou，H.F.，Jia，L.，Zhang，T.T.：An efficient protocol for the private comparison of equal information based on four-particle entangled W state and Bell entangled states swapping.Int J Theor Phys，2014，53(7)：2167-2176

[32]Liu，W.，Wang，Y.B.，Jiang，Z.T.：An efficient protocol for the quantum private comparison of equality with W state.Opt Commun，2011，284：3160-3163

[33]Zhang，W.W.，Li，D.，Li，Y.B.：Quantum private comparison protocol with W States.Int J Theor Phys，2014，53(5)：1723-1729

[34]Ji，Z.X.，Ye，T.Y.：Quantum private comparison of equal information based on highly entangled six-qubit genuine state.Commun Theor Phys，2016，65：711-715

[35]Sun，Z.W.，Long，D.Y.：Quantum private comparison protocol based on cluster states.Int J Theor Phys，2013，52：212-218

[36]Liu，W.，Wang，Y.B.，Jiang，Z.T.，Cao，Y.Z.：A protocol for the quantum private comparison of equality withχ-type state.Int J Theor Phys，2012，51：69-77

[37]Liu，W.，Wang，Y.B.，Jiang，Z.T.，Cao，Y.Z.，Cui，W.：New quantum private comparison protocol usingχ-type state.Int J Theor Phys，2012，51：1953-1960

[38]Lin，S.，Guo，G.D.，Liu，X.F.：Quantum private comparison of equality withχ-type entangled states.Int J Theor Phys，2013，52：4185-4194

[39]Chang，Y.J.，Tsai，C.W.，Hwang，T.：Multi-user private comparison protocol using GHZ class states.Quantum Inf Process，2013，12：1077-1088

[40]Liu，W.，Wang，Y.B.，Wang，X.M.：Multi-party quantum private comparison protocol usingd-dimensional basis states without entanglement swapping.Int J Theor Phys，2014，53：1085-1091

[41]Wang，Q.L.，Sun，H.X.，Huang，W.：Multi-party quantum private comparison protocol with n-level entangled states.Quantum Inf.Process，2014，13：2375-2389

[42]Cerf，N.J.：Pauli cloning of a quantum bit.Phys Rev Lett，2000，84：4497

[43]Cerf，N.J.：Asymmetric quantum cloning in any dimension.J Mod Opt，2000，47(2-3)：187-209

[44]Cerf，N.J.：Asymmetric quantum cloning machines.Acta Phys Slov，1998，48(3)：115

[45]Karimipour，V.，Bahraminasab，A.，Bagherinezhad，S.：Entanglement swapping of generalized cat states and secret sharing.Phys Rev A，2002，65：042320

[46]Li，C.Y.，Zhou，H.Y.，Wang，Y.，Deng，F.G.：Secure quantum key distribution network with Bell states and local unitary operations.Chin Phys Lett，2005，22(5)：1049

[47]Li，C.Y.，Li，X.Ht.，Deng，F.G.，Zhou，P.，Liang，Y.J.，Zhou，H.Y.：Efficient quantum cryptography network without entanglement and quantum memory.Chin Phys Lett，2006，23(11)：2896

[48]Chen，Y.，Man，Z.X.，Xia，Y.J.：Quantum bidirectional secure direct communication via entanglement swapping.Chin Phys Lett，2007，24(1)：19

[49]Ye，T.Y.，Jiang，L.Z.：Improvement of controlled bidirectional quantum direct communication using a GHZ state.Chin Phys Lett，2013，30(4)：040305

[50]Cai，Q.Y.：Eavesdropping on the two-way quantum communication protocols with invisible photons.Phys Lett A，2006，351(1-2)：23-25

[51]Gisin，N.，Ribordy，G.，Tittel，W.，Zbinden，H.：Quantum cryptography.Rev Mod Phys，2002，74(1)：145-195

[52]Deng，F.G.，Zhou，P.，Li，X.H.，Li，C.Y.，Zhou，H.Y.：Robustness of two-way quantum communication protocols against Trojan horse attack.2005，arXiv：quant-ph/0508168

[53]Li，X.H.，Deng，F.G.，Zhou，H.Y.：Improving the security of secure direct communication based on the secret transmitting order of particles.Phys Rev A，2006，74：054302

[54]Gao，F.，Qin，S.J.，Wen，Q.Y.，Zhu，F.C.：A simple participant attack on the Bradler-Dusek protocol.Quantum Inf Comput，2007，7：329

[55]Gao，F.，Wen，Q.Y.，Zhu，F.C.：Comment on：“quantum exam”[Phys Lett A 350(2006)174].Phys Lett A，2007，360(6)：748-750

[56]Guo，F.Z.，Qin，S.J.，Gao，F.，Lin，S.，Wen，Q.Y.，Zhu，F.C.：Participant attack on a kind of MQSS schemes based on entanglement swapping.The European Physical Journal D，2010，56(3)：445-448

[57]Qin，S.J.，Gao，F.，Wen，Q.Y.，Zhu，F.C.：Cryptanalysis of the Hillery-Buzek-Berthiaume quantum secret-sharing protocol.Phys Rev A，2007，76(6)：062324

[58]Lin，J.，Hwang，T.：An enhancement on Shi et al.’s multiparty quantum secret sharing protocol.Opt Commun，2011，284(5)：1468-1471

[59]Chen，J.H.，Lee，K.C.，Hwang，T.：The enhancement of Zhou et al.’s quantum secret sharing protocol.Int J Mod Phy C，1999，20(10)：1531-1535

技术实现要素：

本发明的目的是设计一种基于d级cat态和d级Bell态纠缠交换的多方量子隐私比较方法，解决多个用户秘密的相等性比较问题。

一种基于d级cat态和d级Bell态纠缠交换的多方量子隐私比较方法，共包括以下七个过程：

S1)P_i(i＝1，2，...，n)产生L个d级Bell态|Ψ(0，0)>。

S2)TP制备L个d级n+1粒子cat态|Ψ(u₀，u₁，...，u_n)>，并将它们安排成一个有序序列其中，上标代表d级n+1粒子cat态在序列中的顺序。然后，TP从每个态中将标签为(j＝1，2，...，L)的粒子取出以构成标签为如下的新序列这些序列分别被表示成S₁，S₂，...，S_n。然后，TP向P_i(i＝1，2，...，n)宣布有序标签为防止窃听，TP制备n组诱骗光子并将第i组随机插入S_i。这里，每个诱骗光子是从集合V₁或V₂中随机选择的一个量子态，其中和且ζ＝e^2πi/d。S_i的新序列被记为S′_i。最后，TP将S′_i发送给P_i。

S3)在证实P_i(i＝1，2，...，n)已经收到所有的粒子后，TP和P_i检查S′_i传送的安全性。具体地，TP向P_i宣布S′_i中诱骗光子的位置和基。根据所宣布的信息，P_i使用TP所宣布的基测量相应的诱骗光子并将测量结果返回给TP。然后，TP验证这些测量结果并检查量子信道是否存在窃听者。如果不存在错误，TP证实量子信道是安全的并进行下一步。否则，她们将中止这次通信并重新开始。

S4)P_i(i＝1，2，...，n)丢弃S′_i中的诱骗光子。然后，P_i编码她的秘密x_i。

对于i＝1，2，...，n：

对于j＝1，2，...，L：

P_i首先设置然后，P_i通过对|Ψ(0，0)>施加产生d级Bell态即其中然后，P_i对cat态中标签为的粒子和她的Bell态中标签为的粒子施加d级Bell态测量，从而知道标签为的粒子的最终态。因此，P_i能利用她产生的Bell态的标签和TP在步骤S2向她宣布的cat态的标签独立决定和

S5)对于j＝1，2，...，L：

所有方一起合作计算和然后，她们向TP宣布和

S6)对于j＝1，2，...，L：

第j个cat态被送回给TP。与步骤S2一样，从集合V₁或V₂中随机选择的诱骗光子被用于确保量子传送的安全性。TP测量他的态，得到标签然后TP计算通过从减去TP能得到

S7)如果modn＝0对于所有的j都成立，TP得出所有方的秘密是一样的；否则，TP得出所有方的秘密并不都是一样的。最后，TP秘密地将比较结果告诉P₁，P₂，...，P_n。

本发明提出一种基于d级cat态和d级Bell态纠缠交换的MQPC方法。本发明的方法只执行一次就能完成n方秘密的相等性比较。除了她们的秘密完全相同的情形，一方不能得到其他方的秘密。除了比较结果，半忠诚TP无法得到关于这些方的秘密的任何信息。

附图说明

图1是一个d级n粒子cat态和一个d级Bell态纠缠交换的图形描述，图2是本发明方法的纠缠交换过程的图形描述。

具体实施方式

下面结合附图和实施例对本发明的技术方案做进一步描述。

1、预备知识

在d级系统(量子底特)，对于d级基态|k>(k∈{0，1，...，d-1})，d阶离散傅里叶变换被定义为

其中ζ＝e^2πi/d。两个集合，和构成了两个非正交基。

文献[42-44]介绍的熟悉的Bell态到量子底特的推广是由构成了两量子底特空间一组标准正交基的d²个最大纠缠态组成的一个集合。它们的显形式是

其中标签u和v从0到d-1。容易地，一个人能得到

一个人能通过对|Ψ(0，0)>施加|U_(u，v)>产生任意Bell态|Ψ(u，v)>，其中

即，

文献[45]介绍的d级n粒子cat态具有如下形式：

其中标签u₁，u₂，...，u_n从0到d-1。这些cat态是标准正交的和完备的。

正如文献[45]提到的，当纠缠交换不涉及cat态的第一个粒子(即，m∈{2，3，...，n})时，一个d级Bell态|Ψ(v，v′)>_s，s′和一个d级n粒子cat态|Ψ(u₁，u₂，...，u_n)>_{1，2，...，n}之间纠缠交换的公式可被表示为

公式(7)的图形描述被描绘在图1[45]中。这里，一个d级n粒子cat态被描绘为一条带n个节点的线，其中第一个节点是实心的，其他节点是空心的。并且，一个d级Bell态被描绘为一条带两个节点的线，其中第一个节点是实心的，另一个节点是空心的。在这个纠缠交换过程中，关于这两个态的标签的简单规则为

u_i→u_i对于i＝2，3，...，m-1，m+1，...，n。 (8)

2、MQPC方法

假设存在n方，P₁，P₂，...，P_n，其中P_i(i＝1，2，...，n)拥有一个秘密x_i。x_i在的二进制表示为其中对于j＝1，2，...，L有也就是，2^L-1≤max{x_i}＜2^L。她们想在一个半忠诚TP的帮助下判断她们的秘密是否相等。对于半忠诚TP，目前有两种定义。第一种是由Chen等[16]首次提出，即TP忠诚地执行方法，记录所有中间计算数据，但在不能与任何人共谋的前提下可能尝试从记录中获得参与方的秘密输入。第二种是由Yang等[26]提出，即TP被允许按照自己意愿错误行事但不能与任何人共谋。直到现在，半忠诚TP的第二种定义已经被广泛地接受为最合理的假设。因此，本发明的方法采用半忠诚TP的第二种定义。

所有参与者执行以下七个步骤来完成隐私比较任务。

S1)P_i(i＝1，2，...，n)产生L个d级Bell态|Ψ(0，0)>。

S2)TP制备L个d级n+1粒子cat态|Ψ(u₀，u₁，...，u_n)>，并将它们安排成一个有序序列

其中，上标代表d级n+1粒子cat态在序列中的顺序。然后，TP从每个态中将标签为(j＝1，2，...，L)的粒子取出以构成标签为如下的新序列

这些序列分别被表示成S₁，S₂，...，S_n。然后，TP向P_i(i＝1，2，...，n)宣布有序标签为防止窃听，TP制备n组诱骗光子并将第i组随机插入S_i。这里，每个诱骗光子是从集合V₁或V₂中随机选择的一个量子态。S_i的新序列被记为S′_i。最后，TP将S′_i发送给P_i。

S3)在证实P_i(i＝1，2，...，n)已经收到所有的粒子后，TP和P_i检查S′_i传送的安全性。具体地，TP向P_i宣布S′_i中诱骗光子的位置和基。根据所宣布的信息，P_i使用TP所宣布的基测量相应的诱骗光子并将测量结果返回给TP。然后，TP验证这些测量结果并检查量子信道是否存在窃听者。如果不存在错误，TP证实量子信道是安全的并进行下一步。否则，她们将中止这次通信并重新开始。

S4)P_i(i＝1，2，...，n)丢弃S′_i中的诱骗光子。然后，P_i编码她的秘密x_i。

对于i＝1，2，...，n：

对于j＝1，2，...，L：

P_i首先设置然后，P_i通过对|Ψ(0，0)>施加产生d级Bell态即

其中

然后，P_i对cat态中标签为的粒子和她的Bell态中标签为的粒子施加d级Bell态测量，从而知道标签为的粒子的最终态。因此，P_i能利用她产生的Bell态的标签和TP在步骤S2向她宣布的cat态的标签独立决定和

S5)对于j＝1，2，...，L：

所有方一起合作计算

然后，她们向TP宣布和

S6)对于j＝1，2，...，L：

第j个cat态被送回给TP。与步骤S2一样，从集合V₁或V₂中随机选择的诱骗光子被用于确保量子传送的安全性。TP测量他的态，得到标签

然后TP计算

通过从减去TP能得到

S7)如果modn＝0对于所有的j都成立，TP得出所有方的秘密是一样的；否则，TP得出所有方的秘密并不都是一样的。最后，TP秘密地将比较结果告诉P₁，P₂，...，P_n。

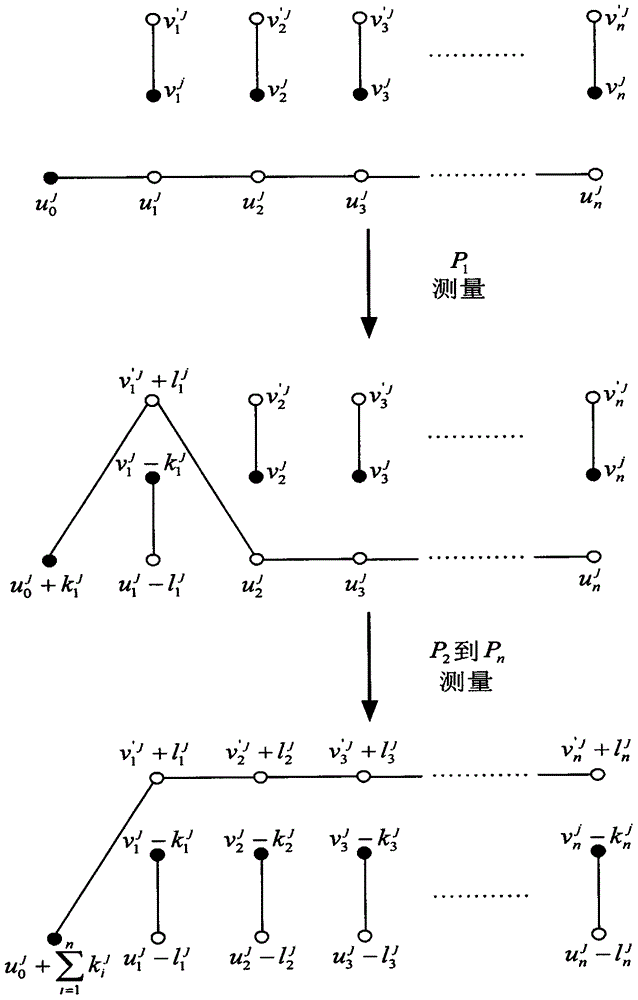
为清晰起见，本发明方法的纠缠交换过程的图形描述进一步在图2中给出。显然，在本发明的方法中，对于j＝1，2，...，L，P_i(i＝1，2，...，n)产生的d级Bell态按照公式(7)与原始d级n+1粒子cat态交换纠缠。

3、分析

3.1输出正确性

在这部分，验证本发明方法的输出是正确的。存在n方，P₁，P₂，...，P_n，其中P_i(i＝1，2，...，n)拥有一个秘密x_i。x_i在的二进制表示为其中对于j＝1，2，...，L有

这里以x_i的第j比特(即)为例说明输出的正确性。P_i通过对|Ψ(0，0)>施加产生来编码(即)。然后，P_i对cat态中标签为的粒子和她的Bell态中标签为的粒子施加d级Bell态测量。这样，cat态中标签为的粒子和她的Bell态中标签为的粒子交换纠缠。在P₁，P₂，...，P_n结束执行d级Bell态测量后，被送回给TP的第j个cat态具有标签TP计算并从中减去以得到显然，可以得到

如果那么如果那么这两种情形意味着modn＝0。否则，modn≠0。可以得出结论，本发明方法的输出是正确的。

3.2安全性

这部分首先指出外部攻击对于本发明的方法是无效的。其次还指出，除了她们的秘密完全相同的情形，一方不能得到其他方的秘密。除了比较结果，半忠诚TP也无法得到关于这些方的秘密的任何信息。

(i)外部攻击

根据本发明方法的每个步骤分析一个外部窃听者窃取这些方秘密的可能性。

在本发明的方法中，步骤S2和S6都有量子底特在量子信道进行传输。一个外部窃听者可能会利用这些量子底特传输通过发起一些著名的攻击，如截获-重发攻击、测量-重发攻击、纠缠-测量攻击等，来提取关于这些方秘密的有用信息。然而，本发明的方法采用诱骗光子技术[46，47]来确保量子底特传输的安全性，其中诱骗光子技术可被视为BB84方法[1]有效的窃听检测方法的一个变种。诱骗光子技术在2级量子系统抗截获-重发攻击、测量-重发攻击、纠缠-测量攻击的有效性也已经在文献[48，49]被详细推演过。可以直接得到，本发明方法采用的诱骗光子技术在d级量子系统中对这些著名攻击同样也是有效的。因此，一个外部窃听者在步骤S2和S6无法窃取任何秘密而不被检测到。

在步骤S4，没有发生传送。因此，一个外部窃听者在这步无法得到任何有用信息。

在步骤S5，P₁，P₂，...，P_n向TP宣布和即使一个外部窃听者听到和仍然无助于她窃取任何秘密或者知道比较结果。

在步骤S7，TP秘密地告诉P₁，P₂，...，P_n比较结果。因此，一个外部窃听者无法在这步知道比较结果。

必须强调的是，在本发明的方法中，量子底特是来回传送的。这样，来自一个外部窃听者的特洛伊木马攻击，包括不可见光子窃听攻击[50]和延迟光子特洛伊木马攻击[51，52]，都应当被考虑进去。防止不可见光子窃听攻击的方法是接收者在她的器件前插入一个过滤器来过滤掉带有不合理波长的光子信号[52，53]。防止延迟光子特洛伊木马攻击的方法是接收者使用一个光子数分割器(Photon number splitter，PNS)来将每个样本量子信号分割成两份并用适当的测量基测量PNS后面的信号[52，53]。如果多光子率高得不合理，这个攻击将被检测到。

(ii)参与者攻击

在2007年，Gao等[54]首先指出，来自一个不忠诚参与者的攻击，即参与者攻击，往往更加强大，应当被投入更多的注意力。直到现在，参与者攻击已经在量子密码分析方面吸引了许多注意力[55-57]。这里，考虑两种情形的参与者攻击。首先，讨论来自一个或更多个不忠诚方的参与者攻击，然后分析来自TP的参与者攻击。

情形1：来自一个或更多个不忠诚方的参与者攻击

两种情形应当被考虑。一种是一个不忠诚方想要窃取其他方的秘密；另一种是多于一个不忠诚方共谋窃取其他方的秘密。有必要强调的是，TP不被允许与任何一方共谋。

(a)来自一个不忠诚方的参与者攻击

既然n方的角色是一样的，不失一般性，在这种情形，只考虑不忠诚P₂想要得到P₁的秘密的情况。

在本发明的方法中，P₁和P₂之间没有任何的量子底特传送。如果P₂尝试去截获步骤S2从TP到P₁或步骤S6从P₁到TP的被传送粒子，正如以上所分析的，她在这两步将不可避免地被当成一个外部窃听者抓住，既然她对诱骗光子的位置和基毫不知情。

在步骤S4，P₂能独立决定和在步骤S5，P₂知道和然而，她对和的知情仍然无助于她得到因为P₂没有机会知道

可以得出结论，不忠诚P₂无法得到P₁的秘密。

(b)来自多于一个不忠诚方的参与者攻击

这里，只考虑这种情形的极端情况，即n-1方共谋来窃取剩余一方的秘密，因为在这种极端情况，不忠诚方具有最大的能量。不失一般性，假设不忠诚P₁，P₂，...，P_i-1，P_i+1，...，P_n共谋来得到P_i的秘密。

首先，如果P₁，P₂，...，P_i-1，P_i+1，...，P_n中的任何一个人尝试去截获步骤S2从TP到P_i或步骤S6从P_i到TP的被传送粒子，正如以上所分析的，她在这两步将不可避免地被当成一个外部窃听者抓住，既然她对诱骗光子的位置和基毫不知情。

其次，在步骤S4，P_m(m＝1，2，...，i-1，i+1，...，n)能独立决定和在步骤S5，当她们一起合作，P₁，P₂，...，P_i-1，P_i+1，...，P_n能从和分别知道和然而，她们仍然不能得到因为她们没有机会知道

可以得出结论，不忠诚P₁，P₂，...，P_i-1，P_i+1，...，P_n不能得到P_i的秘密。

情形2：来自半忠诚TP的参与者攻击

既然TP在本发明的方法中被假设为一个半忠诚第三方，他可能会在不与任何人共谋的前提下尽他自己最大努力去得到P_i的秘密。在步骤S5，TP收到和在步骤S6，TP知道标签然而，由于对不知情，他仍然不能得知即使他知道和

实施例：

1、MQPC方法应用举例

这里以x_i的第1比特(即)为例对本发明的方法进行举例说明。P_i通过对|Ψ(0，0)>施加产生来编码(即)。然后，P_i对cat态中标签为的粒子和她的Bell态中标签为的粒子施加d级Bell态测量。这样，cat态中标签为的粒子和她的Bell态中标签为的粒子交换纠缠。在P₁，P₂，...，P_n结束执行d级Bell态测量后，被送回给TP的第1个cat态具有标签TP计算并从中减去以得到即有如果那么如果那么这两种情形意味着modn＝0。否则，modn≠0。这样，就完成了来自P₁，P₂，...，P_n的第1比特秘密的相等性比较。

2、讨论

由于窃听检测过程能被认为是独立于量子密码方法工作原理的一个标准程序，在不考虑窃听检测过程的前提下对本发明的方法和之前的MQPC方法[39-41]进行比较。将比较结果列在表1中。这里，量子比特效率[8，58，59]被定义为

其中c和t分别是被比较的经典比特数和所消耗的粒子数。文献[41]有两个MQPC方法，在表1中分别被表示为文献[41]-A和文献[41]-B。需要进一步强调的是，文献[39]的MQPC方法实质上在半忠诚TP的第二种定义下是不安全的，与其相反，本发明的方法在这种情况下是安全的。而且，与文献[41]-B的方法需要采用QKD方法不同的是，本发明的方法无需采用QKD方法来确保安全性。

3、总结

本发明提出一种新颖的基于d级cat态和d级Bell态纠缠交换的MQPC方法，其中TP被允许按照自己意愿行事但不能与任何一方共谋。在本发明的方法中，n方采用酉操作来编码她们的秘密，并且只执行一次方法就能比较出她们秘密的相等性。本发明的方法能抵抗外部攻击和参与者攻击。本发明的方法无需采用QKD方法产生秘钥来确保安全性。除了她们的秘密完全相同的情形，一方不能得到其他方的秘密。除了比较结果，半忠诚TP无法得到关于这些方的秘密的任何信息。

表1 本发明的方法与之前的MQPC方法的比较结果