基于改进牛顿迭代的massiveMIMO信号检测方法与流程

本发明属于通信技术领域，涉及一种基于改进牛顿迭代的massivemimo信号检测方法。

背景技术：

massivemimo(多输入多输出)是一种新兴技术，与传统的mimo系统相比，它在能源效率，功耗和链路可靠性方面得到显着改善。因此，大规模mimo系统吸引了学术界和工业界的研究兴趣。已经证明线性检测方案，最小均方误差(mmse)方法，可以达到渐进最优的性能。然而，线性检测算法中仍然涉及大量矩阵求逆运算。为避免矩阵求逆，出现了迭代方法和近似方法两类算法。

当基站天线数量和用户数量之间比值较小时，近似方法通常导致大的残差估计误差以及矩阵乘法的高复杂度。典型的迭代检测方法有雅可比、瑞查森、共轭梯度(cg)，连续超松弛(sor)，高斯-赛德尔等，迭代法可在一定迭代次数内达到mmse检测的性能。所有的算法都在寻求在计算复杂性和期望性能之间的折中。实际中根据复杂度和性能要求选取合适的方法。

技术实现要素：

本发明所针对的是massivemimo系统上行链路中信号检测复杂度高，在实际中难以实现的问题，由于牛顿迭代法可以很好地在脉动阵列和并行计算机上实现，因本发明提供了一种基于牛顿迭代的新的矩阵求逆方法。

本发明的技术方案是：介绍了massivemimo系统中不同类型检测算法之间的关系，接着在此基础提出了一种基于改进牛顿迭代的信号检测方案，其特征在于进行以下步骤：

a.构建系统模型y＝hx+z，其中发射和接收天线数分别为k和n，将传统的mmse检测算法转换为解线性方程组ax＝b的问题；

b.对比近似方法k项纽曼级数展开(nse)和迭代方法的变形形式(假设初始估计x⁽⁰⁾＝p^-1b)，其中a＝p+q，i为单位阵。可以发现迭代方法k次迭代的结果和纽曼级数展开方法k阶(k+1项)近似的结果一样。又因牛顿迭代k次迭代的结果相当于纽曼级数展开方法2^k-1阶近似的结果，因此k次牛顿迭代的结果等价于迭代方法2^k-1次迭代的结果；

c.在迭代方法中当p＝(n+k)i时比p＝d时收敛速度快，因此将现有牛顿迭代方法中的p＝d替换为p＝(n+k)i得到新的改进的牛顿迭代方法，并且在迭代过程中将矩阵-矩阵乘积转换为矩阵-向量乘积。

本发明的有益效果为，介绍了massivemimo信号检测中迭代方法和近似方法之间的关系，并且基于介绍的关系提出了一种改进的牛顿迭代方法。仿真证明提出的牛顿迭代相比现有的迭代方法有更快的收敛速率，并且计算复杂度大幅降低。此外相比纽曼级数近似方法有明显的性能提升，且当接收天线数和发送天线数之间的比值较小时，性能增益更为明显。

附图说明

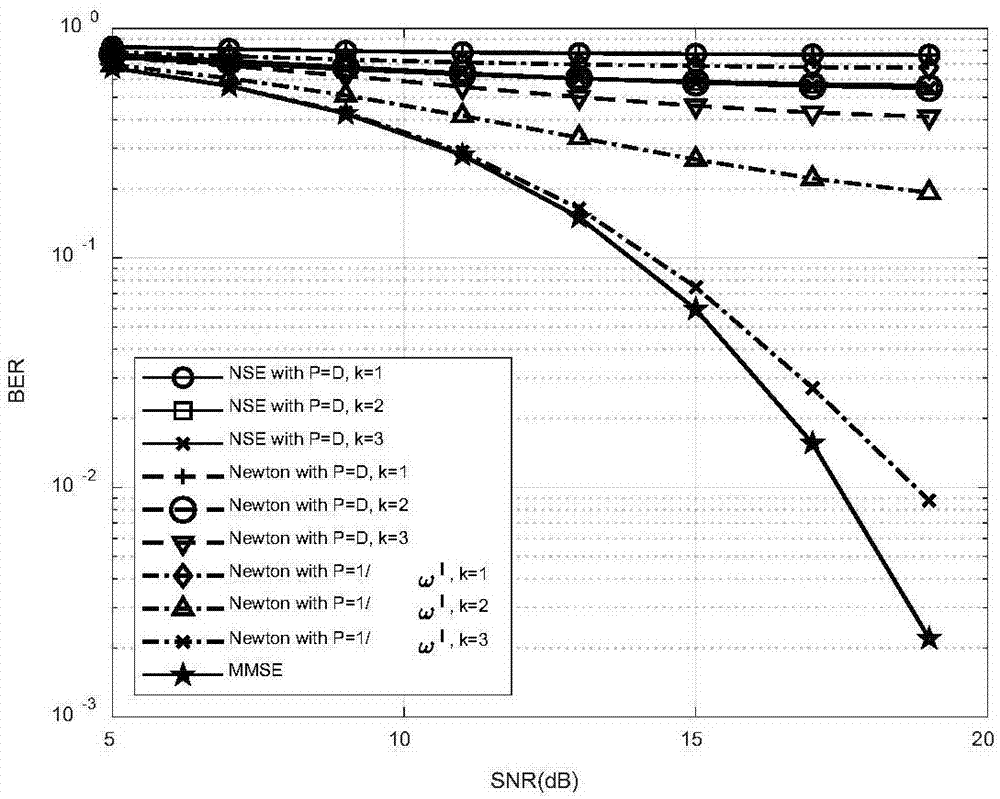
图1当n×k＝64×16时不同方法之间的ber性能比较；

图2当n×k＝128×16时不同方法之间的ber性能比较；

图3当n×k＝256×16时不同方法之间的ber性能比较。

具体实施方式

下面结合附图和实施例，详细描述本发明的技术方案：

本实例具体实施过程如下：

a.系统模型及mmse检测算法

本发明考虑典型的massivemimo系统，其中基站端n根天线同时服务k个单天线用户。经过64qam调制后，发射信号x∈c^k×1经过平坦瑞利信道h∈c^n×k后得到的接收信号y∈c^n×1可以建模为

y＝hx+n,(1)

其中n∈c^n×1表示满足n～cn(0,σ²in)的高斯白噪声。

假设接收端信道估计是完美的，那么mmse检测算法可以表示为

其中b＝h^hy是y的匹配滤波器输出，a＝g+σ²ik表示mmse滤波矩阵，g＝h^hh代表gram矩阵，ik表示k×k的单位阵。此外，直接计算a^-1的复杂度为o(k³)。

b.纽曼级数展开

由于纽曼级数有硬件实现的优势，因此常被用来近似精确矩阵的逆。矩阵a的逆矩阵a^-1具有如下纽曼级数展开形式

(3)式成立还需满足条件当k≤2时k项纽曼级数展开的复杂度为o(k²)。分解矩阵a使得a＝p+q，使得矩阵a和一个非奇异矩阵p近似，那么纽曼级数展开可以写成

纽曼级数近似方法的主要思想时通过截取纽曼级数的前k项来近似矩阵求逆，那么k项近似结果可以表示为

c.迭代方法

迭代方法通过给定初始解然后根据迭代结构逐次逼近期望解。考虑线性方程ax＝b，假设a非奇异，方程组有唯一解x^*。假设a＝p+q，其中p是非奇异的，则等价的迭代法可以表示为

x^(k+1)＝bx^(k)+f,(6)

其中b＝-p^-1q＝i-p^-1a是迭代矩阵，f＝p^-1b，k表示迭代次数。如果则迭代方法收敛。假设初始估计为x⁽⁰⁾＝p^-1b，那么第k次估计结果可由下式给出

显然，迭代方法k次迭代之后的估计结果等价于纽曼级数的k阶(k+1项)展开的结果。

d.牛顿迭代方法

假设p0^-1是a^-1的初次估计，并且第k次牛顿迭代估计可表示为

其收敛的条件是

牛顿迭代法依二次方收敛，而且它的复杂度仅由迭代次数决定。已有文献指出牛顿迭代方法k次迭代之后的估计结果与2^k-1阶(2^k项)纽曼级数展开的结果相等。也就是说，牛顿迭代方法k次迭代之后的结果可以看作是迭代方法2^k-1次迭代之后的结果。

e.提出的牛顿方法

已知雅可比和理查森方法都是静态迭代方法的特殊情形，它们的迭代矩阵分别是bj＝i-d^-1a，br＝i-ωa，其中d是矩阵a的对角元组成的对角矩阵，ω代表松弛因子。由随机矩阵的理论可知，当n和k趋于无穷大时，矩阵a的特征值的最小值和最大值趋于稳定并且收敛于

并且此时由于信道硬化现象，a可以近似为一个对角矩阵，则d≈a＝nik。于是相应的雅可比迭代矩阵bj的特征值为

相应的谱半径为

此外，理查德森方法的最佳松弛因子是根据上述系统特性近似得到的渐进最优松弛因子为

同理得到理查森方法中迭代矩阵的谱半径为明显可以发现

因此，理查德森方法比雅可比方法收敛速度快。根据牛顿方法和迭代方法的关系，在牛顿方法中令可得到收敛速度更快的牛顿迭代方法，因此本发明提出的算法的初始迭代可以表示为

其中q＝a-p，并且对应的估计信号可以表示为

其中接着本发明利用结构(8)进行后续迭代。总而言之，本发明所提出的算法实现可归纳为算法1。

f.复杂度分析

因初始化部分的复杂度和现有的牛顿方法的一样，因此本发明不再细究该部分的复杂度而重点关注迭代部分的复杂度。注意到p是一个对角矩阵，初始估计的涉及3个矩阵-向量乘积，需要k²+2k次乘法。在后续的步骤中，每次迭代涉及2个矩阵-向量乘积和1个常量-向量乘积，需要k²+2k次乘法。因此迭代过程中总的计算复杂度为k(k²+2k)，整体复杂度保持在o(k²)，比k>2的纽曼级数展开方法的复杂度低1个数量级。

g.仿真结果

图1比较了n×k＝64×16时纽曼级数近似算法、现有的牛顿迭代算法以及提出的牛顿迭代算法之间的性能。此外mmse算法的性能也被呈现作为比较基准。可以发现对于收发天线数的比值为4这样一个较小的比值，现有的牛顿迭代和纽曼级数近似方法在较小迭代次数内都有较大的估计残差。而提出的牛顿迭代方法在3次迭代后接近mmse算法的性能。在迭代次数相同时，提出的牛顿迭代方法相较现有的牛顿迭代方法和纽曼级数展开方法都有明显的性能增益。并且在这种系统配置下，纽曼级数展开方法出现性能分层现象无法收敛。现有的牛顿方法收敛缓慢。因此这种情形时提出的牛顿方法是有明显的性能优势的。

相比图1，图2中所有算法的性能因为收发天线数比值增大而都有所提升。从图2中可以发现所有算法的比特错误率都随着展开阶数(迭代次数)的增加而降低。并且3次迭代后提出的牛顿迭代方法的性能达到mmse检测算法的性能，但是纽曼级数展开和现有的牛顿方法的性能仍然和mmse算法的性能有一定差距。给定迭代次数，提出的牛顿方法仍然优于现有的牛顿方法和纽曼级数近似方法。

从图3中可以发现，在收发天线数比值较大时，提出的牛顿方法的性能趋近mmse算法的性能，并且在第2次迭代时当ber为1.5×10^-5时，ber性能损失小于0.27db。此外，提出的牛顿方法2次迭代后的性能比纽曼级数近似方法3次迭代以及现有的牛顿方法2次迭代后的性能好。因此，在这种配置下提出的牛顿方法2次迭代后能以较低的复杂度趋紧mmse算法的性能。

总而言之，提出的算法因其性能和复杂度双重优势可以用于任意系统配置的massivemimo信号检测。而纽曼级数近似方法和现有的牛顿迭代方法仅可用在收发天线数比值较大的情况下。

显然，本领域的技术人员应该明白，本发明的各模块或各步骤可以用通用的计算装置来实现，它们可以集中在单个的计算装置上，或者分布在多个计算装置所组成的网络上，可选地，它们可以用计算装置可执行的程序代码来实现，从而可以将它们存储在存储装置中由计算装置来执行，或者将它们分别制作成各个集成电路模块，或者将它们中的多个模块或步骤制作成单个集成电路模块来实现。这样，本发明不限制于任何特定的硬件和软件结合。另外，本发明提供的思路不仅限于接收端信号检测，还可以用于系统预编码等。