RSA公钥分解和解密方法及系统与流程

本发明涉及信息安全领域，尤其涉及一种rsa公钥分解方法及系统和基于rsa公钥分解的解密方法及系统。

背景技术：

rsa公开密钥加密体系是现代信息社会进行信息安全保障的重大基础设施。该体系于1978年由罗纳德·李维斯特(ronrivest)、阿迪·萨莫尔(adishamir)和伦纳德·阿德曼(leonardadleman)一起提出的[1]。它是一种非对称密钥加密体系。如表1所示，其基本原理是任取两个大素数p、q,计算n＝pq。然后任选一个和(p-1)(q-1)互质的小奇数e，以(e,n)为公钥主体对外发布。同时，在(p-1)(q-1)乘法群中计算e的逆元d，以(d,n)为私钥主体私密保管。该一对密钥可以进行双向加解密。在此理论框架下，如果能够轻易地从公钥中的n(本说明书中的公钥统一理解为n)中得到p和q，也就能够轻易破解出私钥中的d(本说明书中的私钥统一理解为d)。显见，将公钥逆向分解为两个质因子p,q成为rsa体系可靠性的关键。尽管数论研究领域，通过经典的数论计算完成公钥分解理论上可行，但因其计算量巨大而在现实中无法在经典计算机完成。

表1

目前经典计算机采用的公钥质因子分解方法依旧停留在穷举试除法上[2](尽管有些变种，但基本算法方法依旧是穷举法)：用不同的质数去除待分解公钥，如果整除就得到答案。显然这种方法的“探测”次数随着待分解公钥的渐大而变大。如果以待分解公钥n为算法时间复杂度分析的渐进指标，目前所能得到的最佳经典算法通用数域筛选法(generalnumberfieldsieve)的复杂度类是o(exp((logn)^1/3(loglogn)^2/3))[2，3]。可以看出，计算的复杂度呈指数增加。有数据表明，分解rsa-768(一个二进制表示长度为768位的大数)，在目前最快的单机系统上需要2000年的时间[4]。而目前运行的rsa系统通常密钥长度为二进制表示法中的1024位。这使得rsa体系自1978年诞生起，逐渐为人们所接受并成为世界范围内信息安全的重大基础设施，为人类文明进程保驾护航。但我们也不可否认的是：在信息安全领域，研究者一直在尝试寻找新的分解方法或者新的计算方法以期取得私钥破解的突破，并尝试建立新的安全体系。

在新型计算平台和计算模型方面，量子计算的出现给我们带来了rsa公钥体系破解的可能性[5]。量子比特的叠加特性能够支持一个量子比特同时存储0和1两个状态，如果是一个n量子比特系统，则该系统可以同时存储2n个数据。而从计算的角度看，量子计算机可以在一次运算中同时对该2n个数据进行操纵，效果可以比拟2n个经典计算机在同时进行一次计算。这种天然的并行性给量子计算带来了卓越的速度优势[5,6]。在此基础上，1994年，mit应用数学系教授peterwillistonshor提出了可用于公钥质因子分解的shor量子算法[7,8]。该方法首先将公钥n质因子分解问题转成寻找一个函数的周期问题，然后利用量子系统中的量子傅立叶变换来搜寻这个函数的周期。shor算法确实可以在n的多项式时间内完成一个公钥的分解。该算法需要的相互作用的量子比特数目大约是n≈log2n，并且理论上一个512量子比特计算机可以在1秒内完成1024位长度的公钥破解。但是，在当今量子力学最前沿，最好的量子芯片工作在最好的性能下，其量子比特的数量和控制精度远远达不到要求，因此看不到实现的可能。公开的文献报道是2001年，ibm的一个科研小组通过实验验证了shor算法可以将15分解成3×5。综上所述，在量子计算基本原理基础上，突破量子芯片的工作性能并尝试新的计算方法，成为当今rsa公钥质因子分解的工作重点。

技术实现要素：

发明目的：本发明针对现有技术中rsa公钥质因子分解的量子算法均存在的量子比特数要求太多、量子操控精度要求过高的问题，提供一种rsa公钥分解方法及系统和基于rsa公钥分解的解密方法及系统，其基于单量子比特系统，通过将待分解公钥n进行二维厄密矩阵对角化、监测量子系统的能谱、对角矩阵0本征值求解等技术手段，完成公钥n的质因子分解。本发明和经典算法比较，是一种基于单量子比特的质因子分解方法，所需计算时间少，所需存储比特数少，算法效率高，稳定性好。

技术方案：本发明所述的rsa公钥分解方法包括：

(1)获取rsa公钥n；

(2)获取一个小于等于n/3的质因子对<p,q>，并根据该质因子对<p,q>和公钥n形成对应的二维厄密矩阵，同时控制量子系统的外加电磁场，使量子系统的哈密顿量为该二维厄密矩阵，并测量量子系统能谱看该二维厄密矩阵的本征值是否在x＝0处，如果不在，则对其他质因子对<p,q>进行判断，如果在，则判定该质因子对<p,q>为对rsa公钥n进行分解后得到的两个质因子，进行输出。

进一步的，上述步骤(2)具体包括：

(2.1)设置质因子对<p,q>的初始值为<3,3>；

(2.2)判断p是否小于等于n/3，若是，则执行(2.3)，若否，则判定当前rsa公钥n无法分解，结束；

(2.3)根据当前质因子对<p,q>的值和公钥n形成二维厄密矩阵φ：

(2.4)控制量子系统的外加电磁场，使量子系统的哈密顿量为该二维厄密矩阵，并测量量子系统能谱看该二维厄密矩阵的本征值是否在x＝0处；

(2.5)若不在，执行(2.6)；若在，则判断n＝pq是否成立，若成立则判定质因子对<p,q>的当前值为对rsa公钥n进行分解后得到的两个质因子，进行输出，若不成立，执行(2.6)；

(2.6)将q＝q+1，并判断q是否小于等于n/3，若是，则返回执行(2.3)，若否，则执行(2.7)；

(2.7)将p＝p+1,并返回执行(2.2)。

本发明所述的rsa公钥分解系统包括：

公钥获取模块，用于获取rsa公钥n；

公钥分解模块，用于获取一个小于等于n/3的质因子对<p,q>，并根据该质因子对<p,q>和公钥n形成对应的二维厄密矩阵，同时控制量子系统的外加电磁场，使量子系统的哈密顿量为该二维厄密矩阵，并测量量子系统能谱看该二维厄密矩阵的本征值是否在x＝0处，如果不在，则对其他质因子对<p,q>进行判断，如果在，则判定该质因子对<p,q>为对rsa公钥n进行分解后得到的两个质因子，进行输出。

进一步的，所述公钥分解模块具体包括：

初始值设定单元，用于设置质因子对<p,q>的初始值为<3,3>；

p值判断单元，用于判断p是否小于等于n/3，若是，则执行二维厄密矩阵形成单元，若否，则判定当前rsa公钥n无法分解，结束；

二维厄密矩阵形成单元，根据当前质因子对<p,q>的值和公钥n形成二维厄密矩阵φ：

量子系统能谱检测模块，用于控制量子系统的外加电磁场，使量子系统的哈密顿量为该二维厄密矩阵，并测量量子系统能谱看该二维厄密矩阵的本征值是否在x＝0处；若不在，执行q值更新单元，若在，执行质因子判定单元；

质因子判定单元，用于判断n＝pq是否成立，若成立则判定质因子对<p,q>的当前值为对rsa公钥n进行分解后得到的两个质因子，进行输出，若不成立，执行q值更新单元；

q值更新单元，用于将q＝q+1，并判断q是否小于等于n/3，若是，则返回执行二维厄密矩阵形成单元，若否，则执行p值更新单元；

p值更新单元，用于将p＝p+1,并返回执行p值判断单元。

本发明所述的rsa解密方法包括：

(1)采用上述rsa公钥分解方法对rsa公钥n进行分解，得到两个质因子p,q；

(2)根据所述质因子p,q采用以下方式计算得到私钥d：

d＝e^-1(mod(p-1)(q-1))

式中，e为与(p-1)(q-1)互质的奇数；

(3)获取待解密的密文数据c，并采用以下公式将密文数据c解密为明文数据m：

m＝c^dmodn。

本发明所述的rsa解密系统包括：

上述rsa公钥分解系统，用于对rsa公钥n进行分解，得到两个质因子p,q；

私钥计算模块，用于根据所述质因子p,q采用以下方式计算得到私钥d：

d＝e^-1(mod(p-1)(q-1))

式中，e为与(p-1)(q-1)互质的奇数；

数据解密模块，用于获取待解密的密文数据c，并采用以下公式将密文数据c解密为明文数据m：

m＝c^dmodn。

本发明的关键点是将待分解公钥和尝试质因数作为矩阵元素，然后建立量子系统，利用量子比特探测矩阵的本征值，从而进行rsa公钥的质因子分解。本发明把公钥的质因子分解和量子探测结合起来，和现有技术完全不同。

将本发明先和经典大数分解筛选方法比较。筛选法是基于经典计算机和数论理论的，它通常选不同数去除待分解的公钥，需要经典cpu一直做试除运算，经过算法的优化处理，给定一个公钥n，分解开销以n的指数形式增长，无法实用化。而本方案是基于量子理论，在量子计算系统内完成的，在3—n/3内枚举两个不同数p、q，设定其厄密矩阵，探测其本征值极值而完成，不需做乘法。两种策略属于完全不同的理论模型和计算系统，本发明具有天然的、本质的优势。如果一定要比较，给定一个公钥n进行质因子分解，经典筛选法乘法耗费时间指数增加，而本方法是线性增加，性能表现极其优越。

再将本发明和量子算法比较。常用的shor算法，分解给定公钥n(假设其二进制表示需要n位)时，首先需要大约n个量子寄存器，将其分为2组，一组放1到r个自然数，然后选择一个任意小于n而且互质的数m，依次求m^r除以n的余数，放入另外一组寄存器。然后进行测量。运算过程中，对第一组寄存器进行量子傅里叶变换大约需要执行n/2个单比特逻辑门和n(n-1)/2个两比特逻辑门操控。shor算法理论上可以证明是指数加速，但是目前最多可用于量子计算的高精度可控量子比特数是10个左右，量子纠缠保持的时间也只有10微秒，而且要实现shor算法还需要冗余比特纠错，以当前技术，能分解的数只能小于20，基本无法实用。

最后与量子绝热算法比较。用量子绝热算法求(n-ab)²的最小值的办法分解。同样随着n增加，量子比特数也线性增加。

而随着量子比特数增加，量子系统的控制精度必定下降。这个广泛存在于现有各种量子系统中的矛盾使现有各种现有可用于rsa公钥质因子分解的量子计算方案均难于进行实际应用。而本发明只需控制单个量子比特，这是目前技术可以做得非常好的。另外，通过不断改进控制、测量方法(这些经典电路可以做得更好)，可以使能分解的公钥不断增大。

有益效果：本发明与现有技术相比，其显著优点是：

(1)本发明只需对一个量子比特进行控制，容易实现，精度高；

(2)本发明只需要扫描可能的质因子对<p,q>，然后测量量子系统能谱，不需要内部存储单元，因此降低了存储单元要求。

(3)本发明没有迭代等过程，不会出现振荡现象，效率更高，稳定性更好。

(4)本发明只需要按要求精度扫描能谱，公钥质因子分解计算速度有质的突破，能够极大推动rsa公钥分解技术的进步，促进rsa公钥体系的健全和健康发展，提升信息时代信息安全基础设施的可靠性。

附图说明

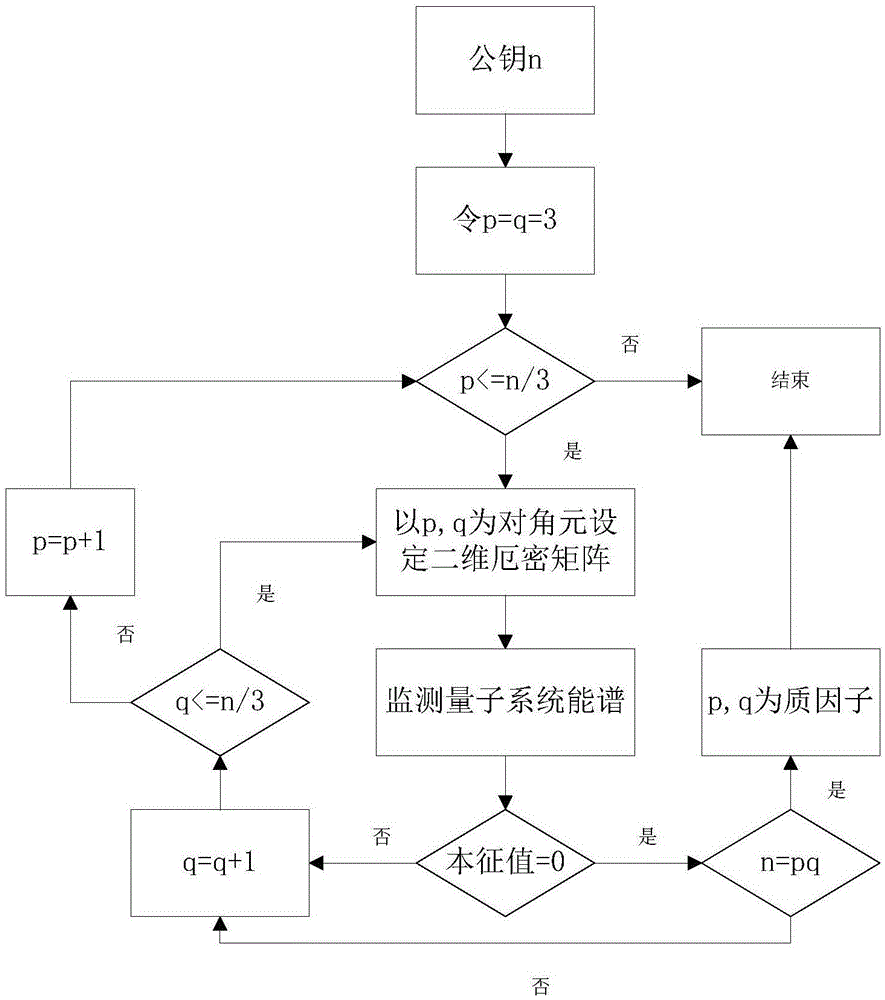
图1是本发明提供的rsa公钥分解方法的一个实施例的流程示意图；

图2是采用图1中方法对公钥15进行分解的结果示意图；

图3是采用图1中方法对公钥35进行分解的结果示意图。

具体实施方式

实施例1

本实施例提供了一种rsa公钥分解方法，如图1所示，包括如下步骤：

(1)获取rsa公钥n；

(2)获取一个小于等于n/3的质因子对<p,q>，并根据该质因子对<p,q>和公钥n形成对应的二维厄密矩阵，同时控制量子系统的外加电磁场，使量子系统的哈密顿量为该二维厄密矩阵，并测量量子系统能谱看该二维厄密矩阵的本征值是否在x＝0处(实验上表现为在0处有一个共振峰的极大值出现)，如果不在，则对其他质因子对<p,q>进行判断，如果在，则判定该质因子对<p,q>为对rsa公钥n进行分解后得到的两个质因子，进行输出。该步骤具体包括：

(2.1)设置质因子对<p,q>的初始值为<3,3>；

(2.2)判断p是否小于等于n/3，若是，则执行(2.3)，若否，则判定当前rsa公钥n无法分解，结束；

(2.3)根据当前质因子对<p,q>的值和公钥n形成二维厄密矩阵φ：

(2.4)控制量子系统的外加电磁场，使量子系统的哈密顿量为该二维厄密矩阵，并测量量子系统能谱看该二维厄密矩阵的本征值是否在x＝0处；

具体的，根据二维厄密对角矩阵的本征值的定义[1]，矩阵本征值x一定满足：

也就是：p×q-(p+q)x+x²-n＝0，观察该方程可以发现，如果方程有x＝0的解，也就是0是矩阵φ的本征值，n＝p×q，n就可以分解成p乘q。另一方面，在量子两态系统中，系统哈密顿量是一个2×2厄密矩阵。不同本征值(或能量)对应于不同的本征态，如果把系统初始化到基态，再用电磁场可以把系统激发到激发本征态。而电磁场的频率正好等于基态到本征态的能量差，这就是共振吸收。一般测量预先无法知道能量差，采用扫描电磁场频率，监测激发态上的布居数，会在某些频率看见共振吸收峰，而这个布居数随频率的变化图就叫做能谱。因此测量能谱其实就给出能量本征值，也就是矩阵的本征值。

(2.5)若不在，执行(2.6)；若在，则判断n＝pq是否成立，若成立则判定质因子对<p,q>的当前值为对rsa公钥n进行分解后得到的两个质因子，进行输出，若不成立，执行(2.6)；

(2.6)将q＝q+1，并判断q是否小于等于n/3，若是，则返回执行(2.3)，若否，则执行(2.7)；

(2.7)将p＝p+1,并返回执行(2.2)。

另外，随待分解公钥n的增大，量子系统的测量误差会增大，可能有一些<p,q>对，即使它们不是公钥n的质因子，但其厄密矩阵本征值也会表现出接近极值0，此时可以利用经典计算机很快检验所得结果，排除这些伪<p,q>对。宏观上说，本方法在扫描<p,q>对时，只需监测对应的厄密矩阵本征值x是否出现极值0，因此可以快速完成该<p,q>对的扫描，因而在<3,3>到<n/3,n/3>的范围内进行质因子<p,q>对的穷尽搜索效率也得到了保障，与此同时，本方法基本不需要内存。此外，扫描中可以有进一步优化的方案，比如偶数和3、5的倍数可以跳过不扫描，从而进一步节省时间。

下面对本实施例进行实验验证。

本发明基于超导量子系统，用单量子比特对rsa公钥质因子分解进行了实验验证。本量子系统中，在其相干时间内，超导量子比特是一个两能级量子系统。它的哈密顿量可以写成[2]

其中h11和h12可以通过微波幅度、频率、位相精确控制。具体是h12正比于微波幅度，h11通过频率调节。我们还可以通过选取不同能量0点来改变对角项。即在h11上增加任意常数。这可以用另外一条附加能级作为能量0点，然后改变附加能级的能量。经过精确设计微波幅度、频率、相位，可以得到需要的哈密顿量：

然后扫描超导量子比特的能谱，测量系统本征值是否在0点，如果在，成功分解；如果不在，改变a、b，重复测量能谱。直到最后得到答案。可以利用简单奇数进行原理验证。

1)n＝15时的质因子数分解：对于n＝15，选取非对角元15^1/2,然后扫描p、q，结果如图2。水平轴分别是改变p和q，方块高度是能量在0点的激发态的布居数，也就是不同参数下本征值为0的几率，当p、q是3和5时x＝0处于极大值，因此质因子是3和5。

2)n＝35时的质因子分解：如果选n＝35，同样可以得到结果p、q是7和5。图3是实验结果的平面图。每一格代表一个参数组合，格子的亮度代表有x＝0本征值的几率。选取不同参数，测量x＝0的本征值的几率，大小用亮度(黄色)表示。可以看出在p、q是7和5时亮度最大，即概率最高，因此，质因子是5和7。

实施例2

本实施例公开了一种rsa公钥分解系统，包括：

公钥获取模块，用于获取rsa公钥n；

公钥分解模块，用于获取一个小于等于n/3的质因子对<p,q>，并根据该质因子对<p,q>和公钥n形成对应的二维厄密矩阵，同时控制量子系统的外加电磁场，使量子系统的哈密顿量为该二维厄密矩阵，并测量量子系统能谱看该二维厄密矩阵的本征值是否在x＝0处，如果不在，则对其他质因子对<p,q>进行判断，如果在，则判定该质因子对<p,q>为对rsa公钥n进行分解后得到的两个质因子，进行输出。

其中，所述公钥分解模块具体包括：

初始值设定单元，用于设置质因子对<p,q>的初始值为<3,3>；

p值判断单元，用于判断p是否小于等于n/3，若是，则执行二维厄密矩阵形成单元，若否，则判定当前rsa公钥n无法分解，结束；

二维厄密矩阵形成单元，根据当前质因子对<p,q>的值和公钥n形成二维厄密矩阵φ：

量子系统能谱检测模块，用于控制量子系统的外加电磁场，使量子系统的哈密顿量为该二维厄密矩阵，并测量量子系统能谱看该二维厄密矩阵的本征值是否在x＝0处；若不在，执行q值更新单元，若在，执行质因子判定单元；

质因子判定单元，用于判断n＝pq是否成立，若成立则判定质因子对<p,q>的当前值为对rsa公钥n进行分解后得到的两个质因子，进行输出，若不成立，执行q值更新单元；

q值更新单元，用于将q＝q+1，并判断q是否小于等于n/3，若是，则返回执行二维厄密矩阵形成单元，若否，则执行p值更新单元；

p值更新单元，用于将p＝p+1,并返回执行p值判断单元。

该实施例与实施例1一一对应，未详尽之处请参考实施例1，不再赘述。

实施例3

本实施例提供了一种rsa解密方法，包括：

(1)采用实施例1的rsa公钥分解方法对rsa公钥n进行分解，得到两个质因子p,q；

(2)根据所述质因子p,q采用以下方式计算得到私钥d：

d＝e^-1(mod(p-1)(q-1))

式中，e为与(p-1)(q-1)互质的奇数；

(3)获取待解密的密文数据c，并采用以下公式将密文数据c解密为明文数据m：

m＝c^dmodn。

实施例4

本实施例提供了一种rsa解密系统，包括：

上述rsa公钥分解系统，用于对rsa公钥n进行分解，得到两个质因子p,q；

私钥计算模块，用于根据所述质因子p,q采用以下方式计算得到私钥d：

d＝e^-1(mod(p-1)(q-1))

式中，e为与(p-1)(q-1)互质的奇数；

数据解密模块，用于获取待解密的密文数据c，并采用以下公式将密文数据c解密为明文数据m：

m＝c^dmodn。

本实施例与实施例3一一对应，未详尽之处请参考实施例3，不再赘述。

以上所揭露的仅为本发明较佳实施例而已，不能以此来限定本发明之权利范围，因此依本发明权利要求所作的等同变化，仍属本发明所涵盖的范围。

参考文献：

1.l.adleman,r.rivest,theuseofpublickeycryptographyincommunicationsystemdesign,ieeecommunicationssocietymagazine16,20–23(1978).

2.j.m.pollard,theoremsonfactorizationandprimalitytesting,proceedingsofthecambridgephilosophicalsociety76,521-228(1974).

3.k.bimpikis,r.jaiswal,modernfactoringalgorithms,atechnicalreportpresentedtotheuniversityofcaliforniasandiego,1-15(2005).

4.https://en.wikipedia.org/wiki/rsa_numbers#rsa-768.

5.m.a.nielsenandi.l.chuang,quantumcomputationandquantuminformation,cambridgeuniversitypress2000.

6.量子计算机研究-原理和物理实现，李承祖等著，科学出版社。

7.petershor,algorithmsforquantumcomputation:discretelogarithmsandfactoring,proceedingsoffocs,124-134(1994).

peterw.shor,polynomial-timealgorithmsforprimefactorizationanddiscretelogarithmsonaquantumcomputer,siamjournaloncomputing,26(5),1484-1509(1997).