一种RSA公钥密码破解方法与流程

本发明涉及整数分解技术领域，特别是涉及一种rsa公钥密码破解方法。

背景技术：

随着素数及算数基本定理的提出，早在公元前300年，整数分解的概念也应运而生。数学在早期的发展主要由日常生活与商业来驱动，而整数分解在这两个领域中均无较大的作用，故而整数分解的研究只能依靠兴趣的驱动。直到20世纪70年代后期，对公钥密码的研究成为了研究整数分解最主要的动力。试除法是目前已知的最早的整数分解方法。费马在1643年提出了一些有关整数分解的思路，这些思路直至今日依旧处于整数分解的核心。费马提出将一个整数写作两平方数之差的形式。如已知合数n，则努力寻找两整数x和y，使得n可被写作，则n的两因子分别为和。

作为一个多产的数学家，欧拉(euler)对整数分解这一问题同样进行了研究，并发展了费马的方法。但欧拉的方法只关注于具有特殊形式的整数，如。欧拉的方法与费马的类似，寻找到两个整数x和y，使得n可以写作如上的形式。用此方法，欧拉在当时成功的分解了一些较大的整数。法国数学家勒让德(legendre)提出了基于平方同余(congruentofsquares)的方法，这一方法是许多现代整数分解的核心。但当时计算能力有限，勒让德的分解方法可分解的整数位数有限。当计算能力较为可观时，勒让德的方法确为最有效的分解方法。1801年，德国数学家高斯出版了他的《算数研究》(disquisitionesarithmeticae)一书。书中提到了许多有关整数分解的思路和方法。高斯的方法非常复杂但可类比于埃氏筛法，简单来说，这种方法通过寻找非常多的模n的二次剩余并以此来排除许多有可能为因子的素数。这种筛选的思路是现代整数分解方法中最为重要的一种思路。在勒让德与高斯之后的很多年中都没有新的整数分解方法出现，即使是勒让德和高斯的方法，由于计算能力有限分解10-15位的整数依然需要大量的工作。

19世纪末期，世界的各地有一些人彼此独立的建立出各种用于进行繁琐计算的机器。1896年，劳伦斯描述了一种机器，它使用可移动的纸带通过可移动的齿轮，其中齿数表示排除模量，纸上的穿透位置代表可接受的余数。这台机器虽然从未真正被建造出来，但它激发了其他人建造出与此类似的机器。1910年之后，莫里斯·克拉奇克(mauricekraitchik)用劳伦斯的思想建造了一台机器。与此同时，geraerardin和carissan兄弟建造了类似的机器，但是在第一次世界大战之后，carissan兄弟建造了第一台可行的筛分机，显示出良好的效果(机器是手动的)。最成功的机器制造者是lehmer，他似乎不知道carissans和kraitchik多年来的工作，他制造了大量的筛分设备，其中一些推动了他那个时代的现代技术。kraitchik和lehmer的机器及其使用的算法与后来开发的二次筛分算法非常相似。

直到20世纪70年代，由于计算机计算能力的提升和公钥密码学的发展，对整数分解的研究具有了实际意义。约翰波拉德(johnpollard)与1974年提出了算法，一年之后他又提出了算法。这两种算法都只针对特殊形式的整数。1975年，morrison和brillhart提出了连分数分解算法，这是第一个适用所有整数的快速分解算法。1982年carlpomerance提出了二次筛法(quadraticsieve)。利用二次筛法，整数分解的位数于1983年提升至71bits。1988年8月31日，约翰波拉德(johnpollard)给a.m.odlyzko写了一封信，并将其拷贝转呈给了richardp.brent，j.brillhart，h.w.lenstra，c.p.schnorr和h.suyama。在这封信中，johnpollard提出了利用代数数域分解特殊形式的整数的思路。不久之后，数域筛法被正式提出。数域筛法是一种最复杂的整数分解算法但却是目前最快速的整数分解算法，数域筛法目前成功分解了768bits。然而数域筛法是概率性整数分解方法，具有一定的随机性，因此目前在整数分解领域也鲜有突破。

技术实现要素：

本发明的目的在于避免现有技术的不足之处而提供一种rsa公钥密码破解方法。

为解决上述技术问题，本发明采用的一个技术方案是：提供一种rsa公钥密码破解方法，包括：

将自然数以不同素数阶乘为间隔划分区域，并根据区域大小及区域边界建立素数阶乘表；其中，素数阶乘表的构建原理为：各列第一行中的整数表示前n个素数阶乘的乘积，记作pn！，各列中其余行中的数为第一行的数依次与不大于第n+1个素数pn+1的正整数相乘的乘积；

获取rsa公钥密码的模数，将模数记为m，对m开方并取整，并计算的位数，记其位数为s；

利用素数阶乘表中对应数位数列s列的第一行元素整除

其中，q表示第s列选择第q行的数字作为后续寻找素因子的中间数；

以第s列第q行作为中间数，在第q行的上下两个方向选择一个整数a0和b0相乘，并与中间数作差，遍历所有可能取值情况，选择差值最小的一组数；

在第s-i列寻找两整数ai和bi，使得(a0+a1+…+ai)·(b0+b1+…+bi)与rsa公钥密码的模数m的差值最小；若任选两整数都有(a0+a1+…+ai)·(b0+b1+…+bi)＞m，则此列中仅挑选一个数，将另一整数设为0，即

(a0+a1+…+ai-1+0)·(b0+b1+…+bi-1+bi)

或

(a0+a1+…+ai-1+ai)·(b0+b1+…+bi-1+0)

以此步骤逐列递减至第二列；

获取rsa公钥密码的模数，将模数记为m，对m开方并取整，并计算的位数，记其位数为s；

利用素数阶乘表中对应数位数列s列的第一行元素整除

其中，q表示第s列选择第q行的数字作为后续寻找素因子的中间数；

以第s列第q行作为中间数，在第q行的上下两个方向各选择一个整数a0和b0相乘，并与中间数作差，遍历所有可能取值情况，选择差值最小的一组数；

在第s-i列寻找两整数ai和bi，使得(a0+a1+…+ai)·(b0+b1+…+bi)与rsa公钥密码的模数m的差值最小；若任选两整数都有(a0+a1+…+ai)·(b0+b1+…+bi)＞m，则此列中仅挑选一个数，将另一整数设为0，即

(a0+a1+…+ai-1+0)·(b0+b1+…+bi-1+bi)

或

(a0+a1+…+ai-1+ai)·(b0+b1+…+bi-1+0)

以此步骤逐列递减至第二列；

判断模数m的素因子类型，若m为m＝6n+1型整数，则分别在属性列中6n+1型素数中寻找两整数α1和α2或ε1和ε2，使得

(a0+a1+…+ai+α1)·(b0+b1+…+bi+α2)＝m

或

(a0+a1+…+ai+ε1)·(b0+b1+…+bi+ε1)＝m

若m为m＝6n-1型合数，则在属性列的6n+1区域和6n-1区域分别各寻找一个整数α1和ε1，使得满足

(a0+a1+…+ai+α1)·(b0+b1+…+bi+ε1)＝m

或

(a0+a1+…+ai+ε1)·(b0+b1+…+bi+α1)＝m

则找到模数m的两个素因子，实现对rsa公钥密码的破解。

区别于现有技术，本发明的rsa公钥密码破解方法通过事先建立素数阶乘表，只需234列的表格即可囊括所有617位十进制数位的整数(rsa-2048是617位)的素因子组合方式，即分解最大617位十进制数位的整数最多只需要遍历132列左右的素数阶乘表，找到每列中的备选数并相加即可。与传统需要遍历所有不大于的试除整数分解方法相比，降低了比较次数和计算量。为rsa加密算法的安全性分析提供了有益参考；本发明是一种可快速分解两因子位数较接近的合数的方法，其主要应用在rsa大模数分解的场景中，对利用分解大模数破解rsa密码体制的攻击方法有推进作用。

附图说明

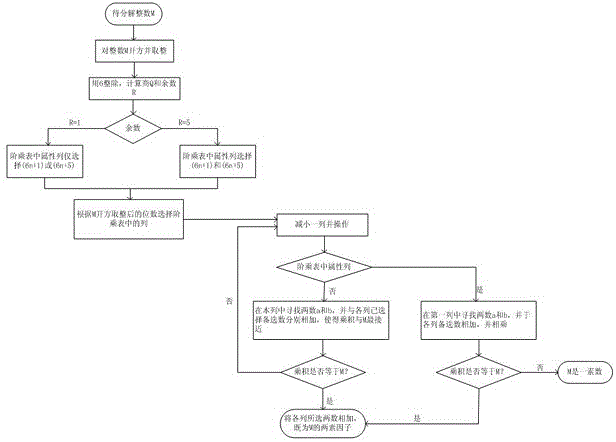
图1是本发明提供的一种rsa公钥密码破解方法的逻辑示意图；

图2是本发明提供的一种rsa公钥密码破解方法中各列选择备选数的流程示意图。

具体实施方式

下面结合具体实施方式对本发明的技术方案作进一步更详细的描述。显然，所描述的实施例仅仅是本发明的一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动的前提下所获得的所有其他实施例，都应属于本发明保护的范围。

如图1所示，本发明提供一种rsa公钥密码破解方法，包括步骤：

将自然数以不同素数阶乘为间隔划分区域，并根据区域大小及区域边界建立素数阶乘表；其中，素数阶乘表的构建原理为：各列第一行中的整数表示前n个素数阶乘的乘积，记作pn！，各列中其余行中的数为第一行的数依次与不大于第n+1个素数pn+1的正整数相乘的乘积；

获取rsa公钥密码的模数，将模数记为m，对m开方并取整，并计算的位数，记其位数为s；

利用素数阶乘表中对应数位数列s列的第一行元素整除

其中，q表示第s列选择第q行的数字作为后续寻找素因子的中间数；

以第s列第q行作为中间数，在第q行的上下两个方向选择一个整数a0和b0相乘，并与中间数作差，遍历所有可能取值情况，选择差值最小的一组数；

在第s-i列寻找两整数ai和bi，使得(a0+a1+…+ai)·(b0+b1+…+bi)与rsa公钥密码的模数m的差值最小；若任选两整数都有(a0+a1+…+ai)·(b0+b1+…+bi)＞m，则此列中仅挑选一个数，将另一整数设为0，即

(a0+a1+…+ai-1+0)·(b0+b1+…+bi-1+bi)

或

(a0+a1+…+ai-1+ai)·(b0+b1+…+bi-1+0)

以此步骤逐列递减至第二列；

获取rsa公钥密码的模数，将模数记为m，对m开方并取整，并计算的位数，记其位数为s；

利用素数阶乘表中对应数位数列s列的第一行元素整除

其中，q表示第s列选择第q行的数字作为后续寻找素因子的中间数；

以第s列第q行作为中间数，在第q行的上下两个方向各选择一个整数a0和b0相乘，并与中间数作差，遍历所有可能取值情况，选择差值最小的一组数；

在第s-i列寻找两整数ai和bi，使得(a0+a1+…+ai)·(b0+b1+…+bi)与rsa公钥密码的模数m的差值最小；若任选两整数都有(a0+a1+…+ai)·(b0+b1+…+bi)＞m，则此列中仅挑选一个数，将另一整数设为0，即

(a0+a1+…+ai-1+0)·(b0+b1+…+bi-1+bi)

或

(a0+a1+…+ai-1+ai)·(b0+b1+…+bi-1+0)

以此步骤逐列递减至第二列；

判断模数m的素因子类型，若m为m＝6n+1型整数，则分别在属性列中6n+1型素数中寻找两整数α1和α2或ε1和ε2，使得

(a0+a1+…+ai+α1)·(b0+b1+…+bi+α2)＝m

或

(a0+a1+…+ai+ε1)·(b0+b1+…+bi+ε1)＝m

若m为m＝6n-1型合数，则在属性列的6n+1区域和6n-1区域分别各寻找一个整数α1和ε1，使得满足

(a0+a1+…+ai+α1)·(b0+b1+…+bi+ε1)＝m

或

(a0+a1+…+ai+ε1)·(b0+b1+…+bi+α1)＝m

则找到模数m的两个素因子，实现对rsa公钥密码的破解。

本发明的目的在于利用素数阶乘构造的素数阶乘表分解大整数，使得分解大整数的复杂度降低。

概括地说，本发明方法包括两部分：

1)构造分解大整数的素数阶乘表；

2)利用素数阶乘表分解rsa的模。

由薛氏筛法可知，可将全体素数表示为α＝6n+1型与ε＝6n-1型素数。

α＝6n+1型合数m有两种素因子乘积形式，分别为：

(1)m＝(α·α)＝(6n1+1)(6n2+1)＝6(6n1n2+n1+n2)+1；

(2)m＝(ε·ε)＝(6n1-1)(6n2-1)＝6(6n1n2-n1-n2)+1；

ε＝6n-1型合数m有一种素因子乘积形式，为：

m＝(α·ε)＝(6n1+1)(6n2-1)＝6(6n1n2+n1-n2)-1

由上述两条性质，已知合数m类型，可推知其两素数因子的类型。

在构造素数阶乘表时，如表1所示。只有素数构成的阶乘为素数阶乘，其中pn为第n个素数值，令pn！表示前n个素数的素数阶乘，则pn！＝p1*p2…pn。

表1素数阶乘表

在表1中，从第二列开始，第n列的第一行表示前n+1个素数的素数阶乘。如p3！＝2*3*5＝30，p4！＝2*3*5*7＝210，p5！＝2*3*5*7*11＝2310，…，依此类推剩余诸列。每一列的值分别表示当前素数阶乘作为基数的倍数积。如第n列中行号分别与素数阶乘的乘积，其中行号最大值是第n+2个素数值，依此类推剩余诸列。

依此逻辑构造如表1的分解大整数需要的素数阶乘表。

在素数阶乘表中属性列的使用过程中，首先通过一个示例引出素因子范围的概念。

如第二列第1行的数30与属性列第1行的数7相加可得37，可表示为：

p3！·1+7＝2×3×5×1+7＝(2×3)×5×1+7＝6×5+7＝6×(5+1)+1.

这符合表中属性列中的6n+1型。

如第二列第7行的数210与属性列第5行的数29相加可得239，可表示为p3！·7+29＝30×7+29＝6×(35+5)-1.

这符合表中属性列中的6n-1型。

将第二列中的所有数分别与属性列中的所有数相加。可依次得到范围是37～241的6n+1型的数，范围是35～239的6n-1型的数，且包括了该范围内的所有素数。

同理，在第三列、第二列与属性列中分别任取一个数并相加，遍历三列中所有可能取值情况，可分别得到范围为247～2551的6n+1型的数，范围是245～2549的6n-1型的数，且包括了该范围内的所有素数。

因在各列中任取一数与属性列中上下两部分相加均为6n+1型与6n-1型的数，可推知，素数阶乘表中各列数字相加可表示所有素数。

本发明提供一个采用本发明方法的分解rsa大整数的实例。

在本实施例中，鉴于实际使用的rsa模数的数位过于庞大，不利于展示，此处选择rsa56(17位十进制位数)整数作为示例，其实施方式和过程与大数位的rsa模数完全相同。

假设待分解整数为m＝19852601254923961。

第一步需确定如表1所示的素数阶乘表的适用范围。

如图1所示，用6整除m得商q＝3308766875820660，余数r＝1。

由薛氏筛法理论，若整数m是合数，则其两因子具有

1.(6n1+1)(6n2+1)形式。

2.(6n1-1)(6n2-1)形式。

由此，如图1所示，利用素数阶乘表分解整数时，属性列仅选择(6n+1)部分，或仅选择(6n-1)的部分。

再将整数m开方并取整，得其位数s为9位。

素数阶乘表中第七列和第八列中包含有9位数，且小于第八列第一行的数223092870。则将素数阶乘表中的第七列选为分解整数的起始列。

接下来从第qil列起，依次向前从各列中挑选两数ai，bi作为各列的备选数，如图2所示。

对于第七列，从第七列中可重复的任选两数相乘并与整数m做差，取乘积不大于整数m的两数作为此列中的两个备选数a7，b7.若找到两数乘积等于m，则结束分解，如图2所示。

此处选择126095970*155195040＝19569469107988800。其中126095970和155195040为本列两备选数。

对于第六列，从第六列中可重复的任选两数分别于第七列中a7，b7相加并相乘，取乘积不大于整数m的两数作为此列中的两个备选数a6，b6.若找到两数乘积等于m，则结束分解。

此处选择(126095970+1021020)(155195040+510510)＝19792820842294500。其中1021020和510510为本列中两备选数。

对于之后第五列至属性列的每一列，均从此列中可重复的选择两数与选择出的备选数相加后相乘，并选择出乘积不大于整数m的两数作为此列中的两个备选数ai，bi。各列过程与结果排列如下：

第五列：

(126095970+1021020+330330)*(155195040+510510+30030)＝19848082299645600.其中330330和30030是本列中的备选数。

第四列：

(126095970+1021020+330330+18480)*(155195040+510510+30030+11550)＝19852432523154000

第三列：

由于此列中任选两数与前几列中的备选数相加，乘积均大于整数m，因此此处仅选择一个备选数，如图2所示，如下，

(126095970+1021020+330330+18480+0)*(155195040+510510+30030+11550+1050)＝19852566362244000。

第二列：

(126095970+1021020+330330+18480+0+90)*(155195040+510510+30030+11550+1050+120)＝19852595675487000。

以上选出了第二列至第七列中各列的备选数。接下来选择属性列中的备选数。

由薛氏筛法可知，属性列中的两备选数仅出自(6n+1)部分或(6n-1)部分。遍历寻找(6n+1)部分内，没有满足条件的备选数。

遍历寻找(6n-1)部分内的数，找到两备选数17和23，如下，

(126095970+1021020+330330+18480+0+90+17)*(155195040+510510+30030+11550+1050+120+23)＝127465907*155748323＝19852601254923961。此时分解整数m完毕。

如图1所示，若遍历完所有列后找不到乘积等于整数m的备选数组合，则整数m无法分解，是一素数。

区别于现有技术，本发明的rsa公钥密码破解方法通过事先建立素数阶乘表，只需234列的表格即可囊括所有617位十进制数位的整数(rsa-2048是617位)的素因子组合方式，即分解最大617位十进制数位的整数最多只需要遍历132列左右的素数阶乘表，找到每列中的备选数并相加即可。与传统需要遍历所有不大于的试除整数分解方法相比，降低了比较次数和计算量。为rsa加密算法的安全性分析提供了有益参考；本发明是一种可快速分解两因子位数较接近的合数的方法，其主要应用在rsa大模数分解的场景中，对利用分解大模数破解rsa密码体制的攻击方法有推进作用。

以上所述仅为本发明的实施方式，并非因此限制本发明的专利范围，凡是利用本发明说明书及附图内容所作的等效结构或等效流程变换，或直接或间接运用在其他相关的技术领域，均同理包括在本发明的专利保护范围内。