基于伊辛模型的大整数分解问题映射方法及系统

1.本发明涉及密码破解技术领域，具体地，涉及基于大整数分解的rsa密码破解技术领域，更为具体地，涉及一种基于伊辛模型的大整数分解问题映射方法及系统。


背景技术：

2.尽管目前计算机的运算能力能够很轻松地计算出任意两个有限大整数的乘积，但它的逆向过程仍然是极为困难的，在有限时间内很难准确计算出一个大整数的因数。因此，大整数分解的困难性被广泛应用在了加密领域，尤其是1977年由ron rivest、adi shamir和leonard adleman共同提出的一种非对称加密算法，简称rsa算法，这种加密算法的安全性正是依靠分解两个大素数之积的困难性实现的。虽然破解rsa算法存在极高的理论难度，但许多研究者一直在探寻有效实现大整数分解的方法，这关系着当今密码体系乃至信息安全的完善与更新。试除法是最早被记录的整数分解方法，但是对于应用在密码体系中的大整数，试除法所需的时间远远超过了一般密码的有效期。数域筛法(nfs)是目前分解较大整数最好的方法，但其过程较为繁琐，包括多项式选择、数对筛选、矩阵生成、矩阵求解、平方根求解五个步骤，并且具有一定的随机性。除此之外，近些年还出现了量子算法对整数进行分解，但由于目前无法做到大量量子比特的稳定控制，量子算法的实际应用还有相当长的距离。
3.伊辛模型最初是一种描述物质铁磁性的物理模型，现在已经发展为有着诸多应用场景的数学计算模型，它包含许多自旋状态为“+1”或“－1”的自旋节点。该模型中，自旋节点间存在两体相互作用，以及外部磁场的作用，从而改变自旋节点的自旋状态，基于这种特性，伊辛模型系统的哈密顿量会逐步降低，直至到达基态。伊辛模型是解决组合优化问题的有效方法，可以将问题参数转化为相互作用强度和外部磁场强度，进而利用求解伊辛模型获取最优解。目前，许多由物理信号(如电信号或光信号等)表征自旋节点的伊辛模型已经被提出，具有计算速度快、能耗低等特性。虽然将大整数分解问题转化为伊辛模型的例子已经有所报道，但现有的方法只有数学上的推导，未形成一般的程序流程，并且需要将多体相互作用转化为二体相互作用，同时对于更大整数的转化，还面临着模型系数过大、精度要求过高等问题。另外，将大整数分解问题转化为伊辛模型后，没有更进一步地分析模型特性，未对迭代过程做出针对性的改进。
4.专利文献cn101814109a(申请号：cn200910078286.4)公开了一种基于dna自组装计算的分解大整数的方法，所述方法包括以下步骤：基于dna自组装技术构建分解整数的逻辑运算架构；形成初始的运算tile，包括起始tile、计算tile和数据传递tile；在预先设定的实验条件下，控制温度以及溶液的浓度，保证dna自组装顺利完成组装；解的检测，寻找出运算完整的自组装结构，分离并提取其中的报告链，根据编码原则读取结果。但该发明没有引入特定的计算模型，没有构建只含有二次项、一次项和常数项的损失函数。


技术实现要素：

5.针对现有技术中的缺陷，本发明的目的是提供一种基于伊辛模型的大整数分解问题映射方法及系统。
6.根据本发明提供的一种基于伊辛模型的大整数分解问题映射方法，包括：
7.步骤s1：对二进制乘法竖式中的每个中间项引入辅助变量，构建辅助块，对每块所得到的损失函数进行形式上的等价替换，使其满足伊辛模型的形式要求，将各块的损失函数相加并作变量代换，化简得到伊辛模型的哈密顿量表达式；
8.步骤s2：根据不同自旋状态下哈密顿量的取值及其范围的分布特征，采取由少到多地更新自旋状态的技术方案，并在特定情况下改变判别条件，使其能够跳出局部最优解，直至伊辛模型到达自旋基态；
9.步骤s3：获取两个素因子信息，实现大整数分解，进一步由欧拉公式和密码系统中开放的公钥得到rsa加密算法中的私钥，使用私钥将密文信息转换为原始明文信息，实现对rsa密码系统的破解。
10.优选地，在所述步骤s1中：
11.针对每个辅助块产生特定形式的损失函数，代入边界条件，并对每个损失函数进行形式上的等价替换，使其不包含二次项以上的高次项，满足伊辛模型的形式要求，进而将全部的损失函数相加、变量代换、化简，得到伊辛模型的哈密顿量表达式，提取出相互作用矩阵j和外部磁场向量h，将大整数分解问题转化为寻找该伊辛模型自旋基态的求解问题；
12.所述的转化过程是通过固定流程实现的，适用于任意大整数，在计算机内程序化完成，针对特定的大整数，不需要单独分析或推导中间过程，能够直接得到对应的伊辛模型；
13.所述的辅助变量是依据两个因数的二进制乘法竖式中的每个中间项a
ibj
逐个引入的，即y
i,j
和z
i,j
，其中y
i,j
为上方辅助块中的二进制变量相加所得的最低位结果，z
i,j
为右方辅助块中的二进制变量相加所得的进位，a
ibj
、y
i,j
、z
i,j
三项构成一个辅助块，产生损失函数；
14.所述的损失函数的形式为f
i,j
＝(a
ibj
+y
i,j
+z
i,j-y
i+1,j-1-2z
i-1,j
)2，等价替换后的形式为
15.所述的等价替换后的损失函数不含有二次以上的项，无需降次操作，并且将其全部相加、化简、变量代换后所得哈密顿量表达式中，变量的系数大小被限制在预设范围，所得伊辛模型的相互作用矩阵j和外部磁场向量h的元素大小也是有限范围的。
16.优选地，步骤s1.1：将所要分解的目标大整数表示为二进制形式，记录位数为w；
17.步骤s1.2：假设目标大整数的两个因数的二进制位数分别是k和h，二进制形式从高位到低位分别为a1,a2,
…
,ak和b1,b2,
…
,bh；
18.步骤s1.3：对于两个因数的二进制乘法竖式中的每个中间项a
ibj
，逐个引入辅助变量y
i,j
和z
i,j
，并将a
ibj
、y
i,j
、z
i,j
三项作为一个辅助块；
19.步骤s1.4：每个辅助块产生一个损失函数，对于边界上的辅助块，根据损失函数的形式引入额外的辅助变量，并代入边界条件；
20.步骤s1.5：对每块得到的损失函数进行形式上的等价替换，使其只包含二次项；
21.步骤s1.6：将各个替换后的损失函数相加并进行变量代换，然后化简得到伊辛模型的哈密顿量表达式；
22.步骤s1.7：表达式中的各个变量作为自旋节点，分别提取二元二次项系数和一次项系数组成伊辛模型的相互作用矩阵j和外部磁场向量h，并将其余的不变量部分的和记为c。
23.优选地，在所述步骤s2中：
24.步骤s2.1：随机产生初始自旋状态，根据得到的伊辛模型计算出哈密顿量；
25.步骤s2.2：每次改变x个自旋，x的初始值为1，随着同一个自旋状态的改变次数增多，使x逐渐增大；
26.步骤s2.3：若改变后的哈密顿量减小，则接受这次对自旋状态的改变，并将x重置为1，否则继续保持改变前的自旋状态；
27.步骤s2.4：若x到达一定值仍未被重置，则降低接受自旋状态改变的判别标准，直到x被重置；
28.步骤s2.5：重复流程步骤s2.2-步骤s2.4，直到自旋状态对应的哈密顿量为-c，说明此时伊辛模型已到达自旋基态，包含目标大整数的两个素因子信息，则实现大整数分解。
29.优选地，所述的降低接受自旋状态改变的判别标准，通过设置一个跳出局部最优解所需的判别能量e_jump，使当前自旋状态所对应的哈密顿量不再是计算得到的，而是将其直接设为e_jump，然后重复迭代过程，直至再次更新哈密顿量得以实现。
30.优选地，模块m1：对二进制乘法竖式中的每个中间项引入辅助变量，构建辅助块，对每块所得到的损失函数进行形式上的等价替换，使其满足伊辛模型的形式要求，将各块的损失函数相加得到伊辛模型的哈密顿量表达式；
31.模块m2：根据不同自旋状态下哈密顿量的取值及其范围的分布特征，采取由少到多地更新自旋状态的技术方案，并改变判别条件，使其能够跳出局部最优解，直至伊辛模型到达自旋基态；
32.模块m3：获取两个素因子信息，实现大整数分解，进一步由欧拉公式和密码系统中开放的公钥得到rsa加密算法中的私钥，使用私钥将密文信息转换为原始明文信息，实现对rsa密码系统的破解。
33.优选地，在所述模块m1中：
34.针对每个辅助块产生特定形式的损失函数，代入边界条件，并对每个损失函数进行形式上的等价替换，使其不包含二次项以上的高次项，满足伊辛模型的形式要求，进而将全部的损失函数相加、变量代换、化简，得到伊辛模型的哈密顿量表达式，提取出相互作用矩阵j和外部磁场向量h，将大整数分解问题转化为寻找该伊辛模型自旋基态的求解问题；
35.所述的转化过程是通过固定流程实现的，适用于任意大整数，在计算机内程序化完成，针对特定的大整数，不需要单独分析或推导中间过程，能够直接得到对应的伊辛模型；
36.所述的辅助变量是依据两个因数的二进制乘法竖式中的每个中间项a
ibj
逐个引入的，即y
i,j
和z
i,j
，其中y
i,j
为上方辅助块中的二进制变量相加所得的最低位结果，z
i,j
为右方辅助块中的二进制变量相加所得的进位，a
ibj
、y
i,j
、z
i,j
三项构成一个辅助块，产生损失函数；
37.所述的损失函数的形式为f
i,j
＝(a
ibj
+y
i,j
+z
i,j-y
i+1,j-1-2z
i-1,j
)2，等价替换后的形式为
38.所述的等价替换后的损失函数不含有二次以上的项，无需降次操作，并且将其全部相加、化简、变量代换后所得哈密顿量表达式中，变量的系数大小被限制在预设范围，所得伊辛模型的相互作用矩阵j和外部磁场向量h的元素大小也是有限范围的。
39.优选地，模块m1.1：将所要分解的目标大整数表示为二进制形式，记录位数为w；
40.模块m1.2：假设目标大整数的两个因数的二进制位数分别是k和h，二进制形式从高位到低位分别为a1,a2,
…
,ak和b1,b2,
…
,bh；
41.模块m1.3：对于两个因数的二进制乘法竖式中的每个中间项a
ibj
，逐个引入辅助变量y
i,j
和z
i,j
，并将a
ibj
、y
i,j
、z
i,j
三项作为一个辅助块；
42.模块m1.4：每个辅助块产生一个损失函数，对于边界上的辅助块，根据损失函数的形式引入额外的辅助变量，并代入边界条件；
43.模块m1.5：对每块得到的损失函数进行形式上的等价替换，使其只包含二次项；
44.模块m1.6：将各个替换后的损失函数相加并进行变量代换，然后化简得到伊辛模型的哈密顿量表达式；
45.模块m1.7：表达式中的各个变量作为自旋节点，分别提取二元二次项系数和一次项系数组成伊辛模型的相互作用矩阵j和外部磁场向量h，并将其余的不变量部分的和记为c。
46.优选地，在所述模块m2中：
47.模块m2.1：随机产生初始自旋状态，根据得到的伊辛模型计算出哈密顿量；
48.模块m2.2：每次改变x个自旋，x的初始值为1，随着同一个自旋状态的改变次数增多，使x逐渐增大；
49.模块m2.3：若改变后的哈密顿量减小，则接受这次对自旋状态的改变，并将x重置为1，否则继续保持改变前的自旋状态；
50.模块m2.4：若x到达一定值仍未被重置，则降低接受自旋状态改变的判别标准，直到x被重置；
51.模块m2.5：重复流程模块m2.2-模块m2.4，直到自旋状态对应的哈密顿量为-c，说明此时伊辛模型已到达自旋基态，包含目标大整数的两个素因子信息，则实现大整数分解。
52.优选地，所述的降低接受自旋状态改变的判别标准，通过设置一个跳出局部最优解所需的判别能量e_jump，使当前自旋状态所对应的哈密顿量不再是计算得到的，而是将其直接设为e_jump，然后重复迭代过程，直至再次更新哈密顿量得以实现。
53.与现有技术相比，本发明具有如下的有益效果：
54.1、本发明完整地表现了一种将大整数分解问题映射为伊辛模型求解问题的一般流程；
55.2、与其他大整数分解方法相比，本发明引入特定的计算模型，分解流程只包括上述两个主要部分，总体上更加简单、直观，第一部分的转换过程直接适用于任何目标大整数，具有通用性，可以直接在计算机中程序化完成，第二部分的计算和迭代过程既可以在通用计算设备上完成，也可以在专用计算平台上实现，具有更加宽泛的硬件实施场景；
56.3、与其他利用伊辛模型解决大整数分解问题的例子相比，本发明直接构建了只含有二次项、一次项和常数项的损失函数，避免了降次操作，同时对于任意大整数，转换得到的伊辛模型的相互作用与外部磁场的取值被限定在有限的范围之内，使它的物理实现和运算更加容易；
57.3、本发明更进一步地针对所得伊辛模型改进了一般的迭代过程，能够更快地找到或接近最优解，并避免陷入局部最优解，提高大整数分解的效率；
58.4、目前，随着伊辛模型相关专用计算设备的发展，有望利用本发明中的方法实现大整数分解记录的突破，从而促进密码学、信息安全等领域的发展。
附图说明
59.通过阅读参照以下附图对非限制性实施例所作的详细描述，本发明的其它特征、目的和优点将会变得更明显：
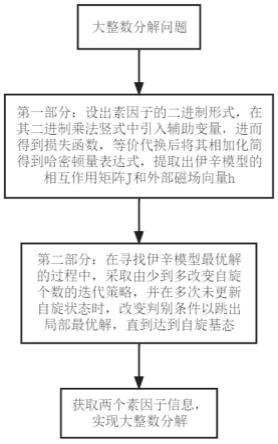
60.图1为本发明提供的大整数分解问题映射方法的整体流程图；
61.图2为本发明中将大整数分解问题转化为伊辛模型求解问题的方法流程图；
62.图3为本发明实施例的二进制乘法竖式中构造辅助块的原理示意图；
63.图4为本发明中对伊辛模型进行迭代寻找自旋基态的方法流程图；
64.图5为本发明实施例的迭代结果示例图。
具体实施方式
65.下面结合具体实施例对本发明进行详细说明。以下实施例将有助于本领域的技术人员进一步理解本发明，但不以任何形式限制本发明。应当指出的是，对本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变化和改进。这些都属于本发明的保护范围。
66.实施例1：
67.本发明引入新的计算模型实现大整数分解问题的映射，整体流程简单直观，迭代过程既可以在通用计算设备上实现，也可以在针对伊辛模型的专用计算平台上完成，丰富了解决大整数分解问题的方法思路和实施场景。
68.一种基于伊辛模型的大整数分解问题映射方法，如图1-图5所示，通过在素因子的二进制乘法竖式中引入辅助变量，将其与中间项逐个构建辅助块，针对每个辅助块产生特定形式的损失函数，代入边界条件，并对每个损失函数进行形式上的等价替换，使其不包含二次项以上的高次项，满足伊辛模型的形式要求，进而将全部的损失函数相加、变量代换、化简，得到伊辛模型的哈密顿量表达式，提取出相互作用矩阵j和外部磁场向量h，大整数分解问题转化为寻找该伊辛模型自旋基态的求解问题；随后针对该伊辛模型进行迭代寻找其自旋基态，采取由少到多地改变当前自旋状态的迭代策略，若改变后的哈密顿量减小则更新自旋状态，同时在一定条件下改变判别条件，使其能够跳出局部最优解，直至伊辛模型到达自旋基态。
69.所述的转化过程是通过固定流程实现的，适用于任意大整数，可以在计算机内程序化完成，针对特定的大整数，不需要单独分析或推导中间过程，便可直接得到对应的伊辛模型。
70.所述的辅助变量是依据两个因数的二进制乘法竖式中的每个中间项a
ibj
逐个引入的，即y
i,j
和z
i,j
，其中y
i,j
为上方辅助块中的二进制变量相加所得的最低位结果，z
i,j
为右方辅助块中的二进制变量相加所得的进位，a
ibj
、y
i,j
、z
i,j
三项构成一个辅助块，产生损失函数。
71.所述的损失函数的形式为f
i,j
＝(a
ibj
+y
i,j
+z
i,j-y
i+1,j-1-2z
i-1,j
)2，等价替换后的形式为
72.所述的等价替换后的损失函数不含有二次以上的项，无需降次操作，并且将其全部相加、化简、变量代换后所得哈密顿量表达式中，变量的系数大小被限制在一定范围，从而所得伊辛模型的相互作用矩阵j和外部磁场向量h的元素大小也是有限范围的。
73.所述的伊辛模型适用于特定的迭代策略，相较于完全随机迭代能够更快地到达基态，并且能够避免陷入局部最优解。
74.所述的迭代策略，具体过程为：
75.1)随机产生初始自旋状态，根据第一部分得到的伊辛模型计算出哈密顿量；
76.2)每次改变x个自旋，x的初始值为1，随着同一个自旋状态的改变次数增多，使x逐渐增大；
77.3)若改变后的哈密顿量减小，则接受这次对自旋状态的改变，并将x重置为1，否则继续保持改变前的自旋状态；
78.4)若x到达一定值仍未被重置，则降低接受自旋状态改变的判别标准，直到x被重置；
79.5)重复流程2)～4)，直到自旋状态对应的哈密顿量为-c，说明此时伊辛模型已到达自旋基态，包含目标大整数的两个素因子信息，则实现大整数分解。
80.所述的降低接受自旋状态改变的判别标准，通过设置一个跳出局部最优解所需的判别能量e_jump，使当前自旋状态所对应的哈密顿量不再是计算得到的，而是将其直接设为e_jump，然后重复迭代过程，直至再次更新哈密顿量得以实现。
81.进一步由欧拉公式和密码系统中开放的公钥得到rsa加密算法中的私钥，使用私钥将密文信息转换为原始明文信息，实现对rsa密码系统的破解。
82.实施例2：
83.实施例2为实施例1的优选例，以更为具体地对本发明进行说明。
84.本发明的目的是提出新的将大整数分解为两个素因数的技术方案，实现大整数分解问题到伊辛模型求解问题的映射，形成相对简单但完备的解决流程，从而使通用计算设备(如电子计算机等)以及各种针对伊辛模型的专用计算设备(如光学伊辛机等)可以直接适用于解决大整数分解问题，进而实现对rsa加密算法的破解。
85.本发明可以根据前后顺序分为两个部分，其中第一部分为大整数分解问题到目标伊辛模型的转换过程，其技术方案是对二进制乘法竖式中的每个中间项引入辅助变量，构建辅助块，并对每块所得到的损失函数进行形式上的等价替换，使其满足伊辛模型的形式要求，最后将各块的损失函数相加并作变量代换，化简得到哈密顿量表达式。第二部分是针对已得到的伊辛模型设计出的合适的迭代过程，根据不同自旋状态下哈密顿量的取值及其范围的分布特征，采取由少到多地更新自旋状态的技术方案，并在一定条件下改变判别条
件，使其能够跳出局部最优解，上述迭代过程能够使伊辛模型更快地找到或接近自旋基态。
86.所述的大整数分解问题到目标伊辛模型的转换，实施流程为：
87.1)将所要分解的目标大整数表示为二进制形式，记录位数为w；
88.2)假设目标大整数的两个因数的二进制位数分别是k和h，二进制形式从高位到低位分别为a1,a2,
…
,ak和b1,b2,
…
,bh；
89.3)对于两个因数的二进制乘法竖式中的每个中间项a
ibj
，逐个引入辅助变量y
i,j
和z
i,j
，并将a
ibj
、y
i,j
、z
i,j
三项作为一个辅助块；
90.4)每个辅助块产生一个损失函数，对于边界上的辅助块，根据损失函数的形式引入额外的辅助变量，并代入边界条件；
91.5)对每块得到的损失函数进行形式上的等价替换，使其只包含二次项；
92.6)将各个替换后的损失函数相加并进行变量代换，然后化简得到伊辛模型的哈密顿量表达式；
93.7)表达式中的各个变量作为自旋节点，分别提取二元二次项系数和一次项系数组成伊辛模型的相互作用矩阵j和外部磁场向量h，并将其余的不变量部分的和记为c。
94.所述的针对已得到伊辛模型设计出的迭代过程，实施流程为：
95.1)随机产生初始自旋状态，根据第一部分得到的伊辛模型计算出哈密顿量；
96.2)每次改变x个自旋，x的初始值为1，随着同一个自旋状态的改变次数增多，使x逐渐增大；
97.3)若改变后的哈密顿量减小，则接受这次对自旋状态的改变，并将x重置为1，否则继续保持改变前的自旋状态；
98.4)若x到达一定值仍未被重置，则降低接受自旋状态改变的判别标准，直到x被重置；
99.5)重复流程2)～4)，直到自旋状态对应的哈密顿量为-c，说明此时伊辛模型已到达自旋基态，包含目标大整数的两个素因子信息，则实现大整数分解。
100.本发明提出了新的将大整数分解为两个素因数的技术方案，得到两个素因子后，可进一步将两个素因子代入欧拉公式，并结合开放的公钥得到rsa加密算法中的私钥信息，再使用私钥将传输的密文信息转换为明文信息，即为被加密的原始数据，至此实现对rsa密码系统的破解。
101.实施例3：
102.实施例3为实施例1的优选例，以更为具体地对本发明进行说明。
103.如图1所示，本发明实现了大整数分解问题到伊辛模型求解问题的映射，并提供了一套完整的解决流程，主要思路是将目标大整数通过确定的程序步骤得到对应的伊辛模型，然后通过计算平台进行迭代获得模型的自旋基态，得到目标大整数的两个素因子。在第一部分中，由目标大整数得到相互作用矩阵j和外部磁场向量h，其主要依据是由乘法竖式确定的损失函数，若损失函数达到0，则说明此时变量的取值正是两个待求的素因子，转换成伊辛模型后，这种状态也正是该模型的基态。第二部分是本发明在第一部分得到伊辛模型后更进一步的优化，设计出寻找伊辛模型自旋基态的迭代策略，伊辛模型能够较快地接近或找到自旋基态，并避免陷入局部最优解。需要说明的是，上述第一部分是确定性的程序流程，可在计算机中程序化实现，对于同一大整数转化得到伊辛模型是固定的；而第二部分
的过程具有一定的随机性，但模型的最优解是确定的。下面具体说明每一部分的实施方式，假设rsa加密算法中的公共模数n为143，因此将对143的分解作为具体实施例辅以解释，应当理解，实际应用的rsa算法中的公共模数量级较大，这里将143作为公共模数是为了便于解释本发明的方法原理，对于更大量级的整数，原理和实施步骤是一样的。
104.如图2所示，第一部分中，首先将待分解大整数用二进制形式表示，记录其二进制位数为w，确定两个素因子的二进制位数分别为k和h，从高位到低位设为a1,a2,
…
,ak和b1,b2,
…
,bh，其中a1,ak,b1,bh可确定为常量1；在两个素因子的二进制乘法竖式中引入辅助变量y
i,j
和z
i,j
，将其和乘法竖式中对应的a
ibj
共同作为一个辅助块；对于每个辅助块，可以确定一个损失函数f
i,j
，其形式为f
i,j
＝(a
ibj
+y
i,j
+z
i,j-y
i+1,j-1-2z
i-1,j
)2，对于在乘法竖式边界的辅助块，需额外生成损失函数中所需的但未被引入的辅助变量，并将其损失函数中的辅助变量用非辅助变量或者已知常量代入，即代入边界条件；对各个损失函数进行形式上的等价替换，不改变函数变量，得到新的f
i,j
形式，其中不包括高于二次的项；将替换后的各个损失函数相加并进行变量代换，使变量的取值由二进制的“1”和“0”变为表征自旋状态的“+1”和“－1”，然后化简得到满足伊辛模型条件的哈密顿量表达式；最后将表达式中的变量表征为伊辛模型的自旋状态，对系数进行提取，其中不同自旋间的二次项系数组成相互作用矩阵j，各个一次项系数组成外部磁场向量h，表达式中构成j和h以外的部分是不变量部分，取值和自旋状态无关，将其取值记为c，用于在第二部分中判断伊辛模型是否到达自旋基态。
105.所述的确定两个素因子的二进制位数，k和h满足k+h＝w或k+h＝w+1，并且在一般情况下，实际应用的大整数的两个素因子差值较小，二进制位数相同的可能性很高，因此初始可以将位数设置为k＝h＝w/2或k＝h＝(w+1)/2，若无法得到正确结果再对两个素因子的位数进行调整；如果大整数分解问题中有额外的位数信息，可以根据额外信息确定两个素因子的二进制位数。
106.如图3所示，在所述的实施例的乘法竖式中构造辅助块，对于每个中间项a
ibj
，引入辅助变量y
i,j
和z
i,j
，并将a
ibj
、y
i,j
、z
i,j
三项作为一个辅助块，其中y
i,j
为上方辅助块中的二进制变量相加所得的最低位结果，z
i,j
为右方辅助块中的二进制变量相加所得的进位。需要说明的是，在此处列出乘法竖式仅为了更清楚地说明本发明的原理，在实际解决大整数分解问题时，直接将要分解的大整数代入如图2所示的程序流程中，即可得到转化后的伊辛模型，无需列出乘法竖式。
107.所述的边界条件，若满足k+h＝w，假设目标大整数的二进制形式从高位到低位分别为t1,t2,
…
,tw；若满足k+h＝w+1，假设目标大整数的最高位t1为0，其实际二进制形式从高位到低位分别为t2,
…
,t
w+1
，则有以下几个边界条件：y
i,0
＝ti；y
k+1,j-1
＝t
k+j
；y
i,h
＝0；z
i,h
＝0；z
k,j
＝0；y
1,h-1
＝0；z
0,j
＝y
1,j-1
；y
k+1,h
＝0。
108.所述的对损失函数进行形式上的等价替换，等价替换后的形式为所述的对损失函数进行形式上的等价替换，等价替换后的形式为
109.如图4所示，第二部分中，首先设置一个跳出局部最优解所需的判别能量e_jump，e_jump的范围由c决定，大于-c但接近-c；随机生成初始的自旋状态，根据第一部分得到的伊辛模型计算出初始自旋状态下的哈密顿量；将每次迭代自旋状态改变的个数设为x，初始
值设为1，然后开始迭代；每次迭代随机改变x个自旋状态，判断改变后模型的哈密顿量是否减小，若减小则接受本次改变，更新自旋状态和对应的哈密顿量，并将x重置为1，若没有减小则进入下面的判断过程：
110.判断x的值是否在一定的迭代次数k(x)后仍未被重置，若否则进行下一次迭代，若是则将x的值增加1，然后根据x的值判断当前是否处于局部最优解，将局部最优解的判断标准设为正整数p，若x《p则说明未处于局部最优解，进行下一次迭代，若x≥p则说明当前状态已处于局部最优解，将x减小1，并降低对当前自旋状态进行更新的判别标准，使当前自旋状态所对应的哈密顿量不再是计算得到的，而是将其直接设为e_jump，然后进行下一次迭代。
111.重复上述迭代过程，直到当前自旋状态的哈密顿量值为-c，说明此时伊辛模型已到达自旋基态，可以获取两个素因子信息，完成大整数分解。
112.所述的判断是否增加x的迭代次数k(x)，k(x)是以x为变量的指数函数，其系数应当与伊辛模型的自旋个数呈正相关。
113.所述的局部最优解的判断标准p，其应当保持较小的数值，具体是对所分解大整数的二进制位数取底数为2的对数，所得数值即为p的大致取值。
114.所述的第二部分中的e_jump、k(x)、p等函数或参数，本发明只给出其定义或取值的标准和参照，其具体式子或取值随着目标大整数的改变而有所不同，并且需要根据迭代结果进行微调，但不应偏离本发明给出的定义或取值范围。
115.如图5所示，本发明的实施例所得伊辛模型的自旋个数为24，c值为44，由图中可见，在经过约47893次迭代后，哈密顿量为-44，伊辛模型到达自旋基态，由此可以得到两个素因子信息，迭代次数47893远小于总共的自旋状态个数2
24
，可知该迭代策略是有效的。
116.所述的两个素因子信息，通过查看伊辛模型到达基态后的自旋状态得出，本实施例的前四位基态自旋状态为“+1，－1，－1，+1”或“－1，+1，+1，－1”，由此可确定两个素因子分别是11和13，第四位后的自旋表示的是辅助变量，与素因子的取值无直接关系，得到两个素因子后，将其代入欧拉公式得rsa加密算法中的私钥指数d与开放的公钥指数e满足代入求出私钥指数d，再使用私钥将传输的密文信息s转换为明文信息m，转换公式为m≡sdmod n，m即为被加密的原始数据，至此已完成对rsa密码系统的破解。
117.本领域技术人员知道，除了以纯计算机可读程序代码方式实现本发明提供的系统、装置及其各个模块以外，完全可以通过将方法步骤进行逻辑编程来使得本发明提供的系统、装置及其各个模块以逻辑门、开关、专用集成电路、可编程逻辑控制器以及嵌入式微控制器等的形式来实现相同程序。所以，本发明提供的系统、装置及其各个模块可以被认为是一种硬件部件，而对其内包括的用于实现各种程序的模块也可以视为硬件部件内的结构；也可以将用于实现各种功能的模块视为既可以是实现方法的软件程序又可以是硬件部件内的结构。
118.以上对本发明的具体实施例进行了描述。需要理解的是，本发明并不局限于上述特定实施方式，本领域技术人员可以在权利要求的范围内做出各种变化或修改，这并不影响本发明的实质内容。在不冲突的情况下，本技术的实施例和实施例中的特征可以任意相互组合。