基于GPU并行优化KNTT算法的全同态加密门自举方法

本发明属于数据加密和数据处理，具体涉及一种基于gpu并行优化kntt算法的全同态加密门自举方法，是一种基于环面的全同态加密方案中的自举加速技术，加速了矩阵与多项式相乘。

背景技术：

1、全同态加密(fully homomorphic encryption，fhe)是一种特殊的加密方案，该加密方案能够支持对密文执行任意次运算(同时包含加法、乘法)，密文运算得到的结果与未加密之前的明文数据执行同样的运算得到的结果相同。为了保证密文的安全性，全同态加密的密文一般会引入噪声。由于在密文运算的过程中，噪声会不断增大，在一定次数的运算之后，过大的噪声会导致密文解密得不到正确的结果，因此全同态加密为了能够支持无限次数的运算，需要一个能够刷新密文噪声的过程，称为自举技术(bootstrapping)。目前全同态加密方案中效率较高的主流方案大多是基于理想格的，在格密码学的方案中，由于密文所处的域为有限域(大多为多项式环)上，所以普遍采用ntt算法来对fhe方案中的自举技术进行优化。ntt被广泛用于实现基于带错误环学习(rlwe)一类的密码方案，但是对于fhe方案的实际应用来说，目前在cpu上使用的ntt算法效率较低，并且ntt算法应用本身存在效率低，密钥和密文尺寸较大，封装成本较高等缺陷，达不到实际使用时的需求。

2、2016年由chillotti等人在文献“faster fully homomorphic encryption:bootstrapping in less than 0.1seconds.asiacrypt,2016”提出了一种全同态加密方案——tfhe。该方案提出的一种高效的门自举技术成功优化了全同态加密的自举算法。其密文基于多项式环，且与该方案门自举技术有关的密文为多项式形式和矩阵的形式。在目前实现tfhe方案的gpu版本cufhe库中，应用了ntt算法实现了门自举过程中的多项式乘法，但是ntt算法并没有改变tfhe方案中的多项式相乘的过程，使其依旧采用较大规模的两个多项式的直接乘法，这导致了基于环多项式的乘法需要与原tfhe方案一样选取较大的模数，方案的参数和密钥以及密文的大小维持在原始的规模没有减小；并且ntt算法只优化了tfhe方案中的多项式乘法，而在tfhe方案中存在的大量的矩阵乘多项式过程，利用原始的ntt算法优化并没有充分发挥gpu并行计算的优势，而且，ntt算法在进行这种大规模的多项式乘法时本身的效率是可以进一步地提高。

3、因此，有必要进一步探究一种能够提升tfhe方案中门自举效率的方案。

技术实现思路

1、本发明的目的在于解决现有tfhe方案中门自举算法的存在效率低的不足之处，而提供一种基于gpu并行优化kntt算法的全同态加密门自举方法。

2、本发明的构思：

3、从背景技术可以看出，ntt算法在对fhe方案进行优化时，效果不明显，仍达不到实际使用时的需求，但是在对tfhe方案进行优化时，有一定的效果(也主要是因为全同态加密方案本身的变化)，然而仅仅优化了多项式乘法这一项内容，对于矩阵乘多项式并没有优化；同时，在gpu版本中，无法充分发挥gpu的并行计算优势，加之，作为ntt算法本身，在进行大规模的多项式乘法时，也是有进一步提升的空间的。因此，本技术拟从ntt算法着手(用karatsuba乘法对其进行不同于原有方法的优化)，进一步提升tfhe方案中门自举算法的效率。

4、为实现上述目的，本发明所提供的技术解决方案是：

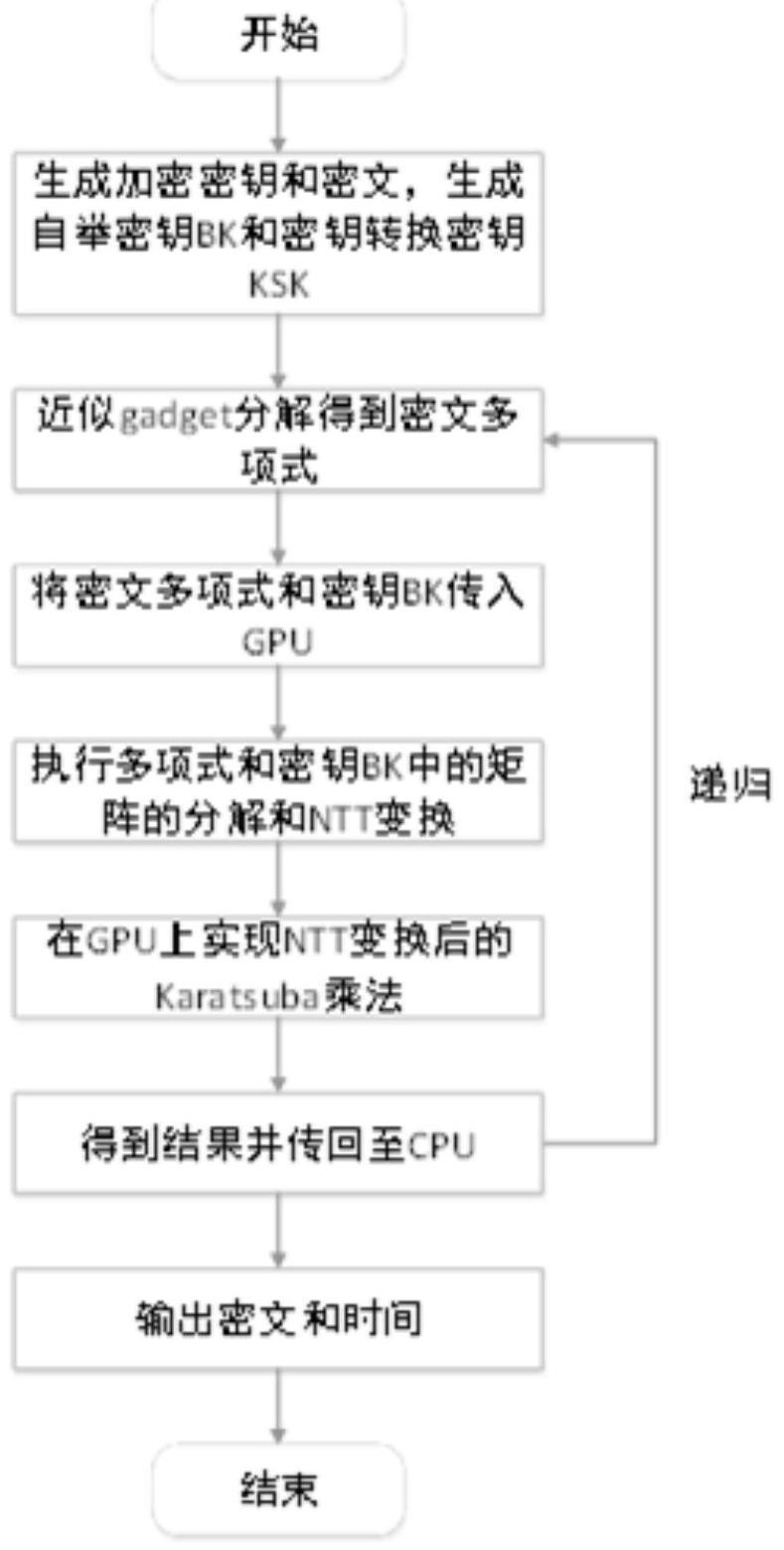
5、基于gpu并行优化kntt算法的全同态加密门自举方法，其特殊之处在于，包括以下步骤：

6、步骤1、门自举初始化

7、定义门自举的初始输入为一个tlwe密文c＝tlwes(μ)＝(a,b)∈tp+1，其中a＝(a1,a2,...,ap)∈tp，t表示实环r/z，e为从高斯分布上选取的噪声；

8、所述tlwe密文对应的明文空间为m，m∈{μ0,μ1}，其中，μ0＝0，μ1∈t，且μ0≠μ1；

9、所述tlwe密文的加密密钥为s＝(s1,s2,...,sp)∈bp，且其对应的明文的取值也为μ0＝0和μ1∈t；

10、1.1)选取用于门自举过程中盲旋转算法的自举密钥

11、自举密钥为p个trgsw密文，p为正整数；

12、所述p个trgsw密文对应的加密密钥为s”∈bn[x]k；

13、其中，k为正整数；n为2的整数次幂，表示trgsw密文中的多项式的项数；

14、每个trgsw密文中对应的明文分别为组成加密密钥s＝(s1,s2,...,sp)∈bp的p个比特，该自举密钥bk＝(bk1,bk2,...,bkp)表示为如下形式：

15、bki＝trgsws'(si),i＝1,2,...,p

16、1.2)选取用于门自举过程中密钥转换算法的转换密钥

17、转换密钥表示为如下形式：

18、ksks'→s＝{kski,j},i＝1,2,...,p,j＝1,2,...,t

19、其中，kski,j∈tlwes(s'i·2-j)，这里p和t均为正整数，t表示密钥转换过程的精度；

20、转换密钥的功能为将密钥s'∈bp变换到步骤1.1)中的加密密钥s∈bp；

21、其中，s'∈bp是trgsw密文对应的加密密钥s”∈bn[x]k经过密钥提取得到的结果，即s'＝keyextract(s”)；这里的密钥提取涉及到两种技术手段——样本提取和密钥提取，样本提取(sample extract)为对trlwe密文中的多项式的系数重新排列，得到对应trlwe明文多项式的某一项的tlwe密文的算法；密钥提取(key extract)是指对trlwe密文的由多项式组成的密钥进行处理，将密钥多项式的系数提取出来得到与样本提取得到的tlwe密文对应的密钥；

22、上述s，s'和s”，其中通过s”进行密钥提取得到s'，通过密钥转换将s'转变为s。

23、步骤1.1)和1.2)中选取的自举密钥和转换密钥是进行接下来初始化和后续步骤中所需要的密钥，步骤1.1)和1.2)介绍了自举密钥和转换密钥的生成过程和详细使用方法和功能；

24、1.3)进行门自举初始化

25、令令为最接近2nai的整数，令为最接近2nb的整数，则初始密文中的元素变为了有初始多项式并且构造(0,v)，0表示n维的0向量，则(0,v)为一个对应明文为多项式v的trlwe密文，得到初始的并将acc0存储在全局内存中；

26、步骤2、近似gadget分解得到密文矩阵和多项式

27、将步骤1初始化得到的acc0，初始密文和自举密钥bk＝(bk1,bk2,...,bkp)作为下述整个过程的输入，令

28、

29、这里将acc进行gadget分解的结果表示为acc＝(a1,a2,...,ak,ak+1)∈tn(x)k+1，其中对于每一个ak＝c0k+c1kx+c2kx2+...+c(n-1)kxn-1,k＝1,2,...,k+1，k代表k中的子项，将多项式ak的全部系数改写为

30、

31、令这里k＝1,2,...,k+1,q＝1,2,...,l，这样可以得到最终结果

32、dech(acc)＝(a11,...,a1l,...,a(k+1)1,...,a(k+1)l)

33、其中，k，l表示近似gadget分解矩阵的大小，均为正整数；

34、就前文提到的密钥bk的子项来说，将与bk中的子项bk1进行相乘即为多项式乘以矩阵的过程；

35、步骤3、利用gpu并使用结合karatsuba乘法的ntt优化算法(kntt算法)实现密文中矩阵与多项式的乘法

36、以karatsuba乘法的分解次数α为基准，设定α的取值范围为α∈{1，2}，执行下述的矩阵与多项式乘法步骤：

37、3.1)将大的多项式和矩阵分解为小的子多项式和矩阵

38、对于步骤2中的和bk1，将其作为输入，设定支持环多项式分解的环同构如下：

39、

40、其中

41、依据上述同构选择α的取值；

42、当α＝1时，上述同构为zq[ξ']＝r，ξ'＝η2；

43、将大的多项式akq进行拆分，即其中，ar为akq拆分多项式后所得的子项，r代表p的子项，ar与n和α的关系为：

44、

45、当α＝1时，akq展开写成如下形式：

46、akq＝a0+η·a1

47、同理，对密钥bk中的子项bk1进行同等拆分；

48、由于bk1为一个矩阵，将其每一行表示为多项式其中，为bk拆分后所得子项，其中与n和α的关系为：

49、

50、当α＝1时，将bk1中的子多项式bk展开写成如下形式：

51、

52、上述的akq∈zq[η]，bk1∈zq[η]k，

53、当α＝2时，上述同构为zq[η]＝zq[ξ'][x]/(x4-ξ')＝r[η]，ξ'＝η4，将大的多项式akq进行拆分，即其中ar为akq拆分多项式后所得的子项，ar中的元素值参考上述ar的通项；将akq展开写成如下形式：

54、akq＝a0+η·a1+η2·a2+η3·a3

55、同理，对密钥bk中的子项bk1进行同等拆分；

56、将其每一行表示为多项式其中为bk拆分后所得子项，中的元素值参考上述的通项；将bk1展开写成如下形式：

57、

58、上述的akq∈zq[η]，bk1∈zq[η]k，b0k,b1k,b2k,b3k,a0,a1,a2,a3∈zq[ξ'],0<k≤k；

59、这样就得到了小多项式ar和然后进行ntt变换和karatsuba乘法；

60、3.2)子多项式的ntt变换

61、以步骤3.1)中得到的子项ar和作为输入进行ntt变换，将ntt过程中的模素数b的原根代入多项式中代替复平面上的单位根进行fft的数学变换即为ntt变换，即：

62、

63、

64、在ntt变换中，这里w为模素数b的一个原根；

65、将多项式分解后得到的每一个子项对应w为模素数b的一个原根；并将ar中的保存在共享内存xi中，i根据α分为r部分；

66、同理，对多项式也进行上述ntt变换，根据bk1的行数k分配线程数，对于整个过程的ntt变换来说，并提前对ntt(ξ)进行计算；

67、当α＝1时，需计算ntt(a0)，ntt(a1)，其中0＜k≤k，共需2k+2次的ntt变换；

68、当α＝2时，则需计算ntt(a0)，ntt(a1)，ntt(a2)，ntt(a3)，其中0＜k≤k，共需4k+4次的ntt变换；

69、这里可以看出α的取值与ntt变换次数的关系；当karatsuba乘法的分解次数为α时，ntt变换为2α(k+1)次；

70、至此，将所得子多项式全部进行了ntt变换；

71、3.3)多项式ntt变换后的karatsuba乘法

72、将该过程的最终结果用多项式形式s表示；

73、利用karatsuba乘法对上述得到的经过ntt变换的子多项式进行计算；

74、该步骤在gpu上实现，基于矩阵bk1的大小安排各个线程，对于一个k×l大小的矩阵bk1来说，共安排k个线程，在每一个线程内，对于矩阵bk1中的每一个多项式和相乘来说，依据α的取值生成如下初始矩阵：

75、当α＝1时，karatsuba乘法为如下形式：

76、

77、这里为了表述清楚，省略了关于原始ntt变换的表示；

78、生成初始矩阵i和初始矩阵e如下：

79、

80、

81、得到最终结果多项式s中的每一个子项如下表示，其中0＜k≤k：

82、

83、这里的karatsuba算法将原本分解后的小多项式之间的乘法由4次变成3次；

84、当α＝2，karatsuba乘法为如下形式：

85、

86、同样省略了多项式关于ntt变换的表示，生成初始矩阵i和初始矩阵e如下：

87、

88、

89、得到最终结果多项式s中的每一个子项如下表示，其中0＜k≤k：

90、

91、这里的karatsuba算法将原本分解后的小多项式之间的乘法由16次变成了9次；

92、对于普遍的karatsuba算法来说，若将一个多项式分解α次，则会得到2α个子多项式，这2α个子多项式进行互相之间的乘法需要4α次的乘法，而karatsuba算法可以将乘法次数减少为3α次；

93、3.4)ntt逆变换

94、根据步骤3.3)中所得的多项式s进行ntt的逆变换，获取多项式乘积最终结果，该结果即为acc1；

95、acc1＝s＝ntt-1(sk(ξ))，其中0＜k≤k；

96、通过上述步骤可以看出，随着α的增大，多项式分解的次数变多，矩阵与多项式相乘的子问题规模变小，所获得的加速也更好。但是其产生的多项式子项变多，这会导致数据传递次数变多，且子项之间所需要的乘法次数也会变多；这同时也会导致初始矩阵i和e的变大；可以很简单地推导出矩阵i的大小为3α×2α，矩阵e的大小为3α×1，且i和e无法利用α简单表示出；当α过大时会导致初始矩阵i和e的初始化求解困难以及矩阵规模大等问题，并且当α较大时，所获得的加速效果会与α＝2时的加速效果接近，所以本发明只考虑了α＝1和α＝2时的情况；

97、步骤4、得到门自举的最终结果

98、4.1)将步骤3中得到的acc1存储在全局内存中，然后用得到的acc1代替acc0，用bk2代替bk1，重复上述步骤2和步骤3，而后将步骤3中得到的结果acc和密钥bk中的子项作为输入一直进行步骤2和步骤3，直到密钥bkp已得到使用，该过程是一个递归的过程，它利用第一个acc和bk密钥的第一个元素来得到第二个acc，而后通过第二个acc和bk密钥的第二个元素得到第三个acc，以此类推，直到bk密钥中的元素均被用到，得到最终的acc结果，即accp；

99、4.2)将最后所得accp进行密文提取，选择accp＝(a'0,a'1,...,a'k)中的每个多项式的常数项组成一个新的密文，并且将最后一项加上μ'，得到密文c'＝(c00,c01,...,c0k+μ')，令其中最终得到门自举的结果，密文为：

100、

101、其中，kskkj即为转换密钥，j表示t中的子项。

102、进一步地，步骤2中，对acc进行近似gadget分解采用的分解基为h∈tn(x)(k+1)l×(k+1)，具体表示形式如下：

103、

104、其中，参数k，l，bg均为正整数，k，l表示近似gadget分解矩阵的大小，bg表示分解矩阵中的元素；

105、将acc看作是一个trlwe密文，对于其中的每一个元素写成如下形式：

106、acc＝(a,b)＝(a1,a2,...,ak,b)∈tn[x]k+1

107、将其中的每一个ai(i＝1,2,..,k)改写为ai,j∈t；

108、令a'i,j作为最接近ai,j的的整数倍，对于每一个a'i,j，将其分解并且写成一个分量和一个gadget的基的一项的乘积，即：

109、

110、其中，分量ai,j,k为[-bg/2,bg/2)内的整数，k＝1,2,...,l；

111、然后，令

112、

113、其中，ui,k∈zn[x],i＝0,1,...,k；

114、将经过这样的近似gadget分解得到的结果acc表示为：

115、dech(acc)＝(a11,...,a1l,...,a(k+1)1,...,a(k+1)l)

116、就前文提到的密钥bk的子项来说，将akq与bk中的子项bki进行相乘即为多项式乘以矩阵的过程。

117、本发明的原理：

118、在tfhe方案中，门自举计算的核心步骤是经过处理后的tlwe密文和由tgsw密文组成的自举密钥的乘法，其本质上为多项式与矩阵的乘法。为了加速这一过程，本发明研究团队不采用原始的ntt算法，而是使用基于karatsuba快速乘法优化的ntt算法，即kntt。该方法由于利用了karatsuba快速乘法在计算多项式相乘时将大的多项式分解为小的子多项式的特性，放松了tfhe方案多项式环上对模数的约束，使得在密码系统中可以选择更小的模数，降低了密钥大小和密文大小，进一步提高相应密码系统的效率。同时，该方法从原来的计算多项式相乘(tlwe密文)扩展到矩阵和多项式的乘法运算(tgsw密文和tlwe密文)，在原方案的基础上省略了ntt变换生成的中间项，统一采用特定的矩阵(矩阵i和矩阵e)进行相乘获得最终结果，大幅简化了算法的步骤，使其运行效率比原始的ntt算法更高。

119、本发明的优点是：

120、针对tfhe方案中的矩阵乘多项式的计算，本发明设计了一种利用karatsuba乘法的ntt算法，并利用gpu的并行计算，将该算法的功能扩展到了矩阵乘多项式的计算之中，此外还引入了基础初始化矩阵，利用矩阵的乘法来代替原始中间生成项，减少了该算法的步骤，提高了tfhe方案门自举的效率。kntt算法在cpu上进行矩阵和多项式的乘法的时间复杂度为o(n2log(n))，本文在实现时间复杂度为o(nlog(n))；并将门自举的运行时间降低到了原本的12.5％。