一种快速生成高概率原根的计算方法、系统及存储介质

本发明涉及网络安全，具体涉及一种快速生成高概率原根的计算方法、系统及存储介质。

背景技术：

1、在离散对数型密码系统中，大质数与原根这两个参数相当重要且关系到系统的安全性。为了降低计算复杂度，现有方法通常先利用概率式的质性判定方法产生，然后再利用费马定理去验证原根的阶是否最大，这两个参数产生的过程都需要用到模指数运算，计算复杂度皆为。然而，前面产生大质数的方法是属于概率式的，后面产生原根的方法却是确定式的，这意味着是不是原根其实也是一个概率问题，这样产生原根的计算复杂度较大，从而导致整体系统的复杂度也较大。

2、而目前验证原根方法为：先将p-1分解后，，然后逐一计算算式是否成立， 1 mod p 或 1 mod p , i=2,3,...k，总共需要k次模指数运算，若所有算式皆成立，才可判定所任选的为原根。

3、其次，当p是一个非常大的质数时，p-1可能包含很大的因子相乘的复合数，这时就很难进行分解，因为这是一个大数分解的数学难题。

4、所以，现有技术方法的缺点有至少如下两点：(1)需要k次模指数运算，每次计算复杂度为，整体计算复杂度过高，特别是在一些计算资源受限的装置中较难实现。(2)若p-1无法完全分解，则无法正确判别原根，且错误概率非常高。

技术实现思路

1、本发明提供了一种在数论中生成和判别原根的计算方法，可直接应用于离散对数型密码系统中，降低信息安全与网络安全所需的计算复杂度。本发明能直接用较低的计算复杂度产生概率式的原根，对降低整体系统复杂度有所助益。

2、有鉴于此，本发明第一方面提供了一种快速生成高概率原根的计算方法，所述方法包括：

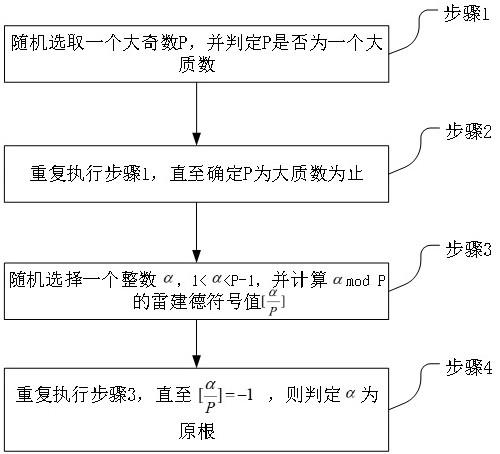
3、步骤1：随机选取一个大奇数p，并判定p是否为一个大质数；

4、步骤2：重复执行步骤1，直至确定p为大质数为止；

5、步骤3：随机选取一个整数，1<<p-1，并计算mod p的雷建德符号值；

6、步骤4：重复执行步骤3，直至，则判定为原根。

7、可选地，结合第一方面，在一种可能的实现方式中，所述方法还包括：确定是一个原根的概率步骤，其中，所述确定是一个原根的概率步骤具体包括：

8、假设，表示存在一个平方根满足：；

9、由于，则，的阶等于，当时，一定不是一个原根；

10、满足的总个数为：，其中，k≥2；

11、其中，阶为原根的非同余整数总个数为：

12、；

13、则隐含是一个原根的概率为：。

14、本发明第二方面提供了一种快速生成高概率原根的计算系统，所述系统包括：存储器和至少一个处理器，所述存储器中存储有指令，所述存储器和所述至少一个处理器通过线路互连；所述至少一个处理器调用所述存储器中的所述指令，以使得所述装置执行如本发明第一方面或第一方面的任意一种可能的实现方式中所述的快速生成高概率原根的计算方法。

15、本发明第三方面提供了一种计算机可读存储介质，所述计算机可读存储介质上存储有计算机程序，所述计算机程序被处理器执行时，实现如本发明第一方面或第一方面的任意一种可能的实现方式中所述的快速生成高概率原根的计算方法。

16、本发明提出的快速判别原根的方法为：直接计算mod p 的雷建德符号值，若，则为原根的正确概率趋近于1。

17、与现有技术对比，本发明所需的计算复杂度仅为，远低于现有技术需要k次的计算复杂度。同时，不需进行p-1的因子分解，易于直接实现。

技术特征：

1.一种快速生成高概率原根的计算方法，其特征在于，所述方法包括：

2.根据权利要求1所述的快速生成高概率原根的计算方法，其特征在于，所述方法还包括：确定是一个原根的概率步骤，其中，所述确定是一个原根的概率步骤具体包括：

3.一种快速生成高概率原根的计算系统，其特征在于，所述系统包括：存储器和至少一个处理器，所述存储器中存储有指令，所述存储器和所述至少一个处理器通过线路互连；所述至少一个处理器调用所述存储器中的所述指令，以执行如权利要求1或2中所述的快速生成高概率原根的计算方法。

4.一种计算机可读存储介质，所述计算机可读存储介质上存储有计算机程序，其特征在于，所述计算机程序被处理器执行时，实现如权利要求1或2中任意一项所述的快速生成高概率原根的计算方法。

技术总结
本发明公开了一种快速生成高概率原根的计算方法、系统及存储介质，所述方法包括：步骤1：随机选取一个大奇数P，并判定P是否为一个大质数；步骤2：重复执行步骤1，直至确定P为大质数为止；步骤3：随机选取一个整数，1<<P‑1，并计算mod P的雷建德符号值；步骤4：重复执行步骤3，直至，则判定为原根。

技术研发人员：彭顺富,廖珮君
受保护的技术使用者：泉州信息工程学院
技术研发日：
技术公布日：2024/1/15