一种基于GPS的车载公路线形测量方法与流程

文档序号：11404729阅读：430来源：国知局

本发明属于交通安全研究领域，具体涉及一种基于gps的车载公路线形测量方法。

背景技术：

在交通安全研究领域，获得公路三维线形是进行后续研究的基础。在公路管理系统中,也常需建立道路路线图形数据库，如基于地理信息系统(gis)的道路安全管理信息系统、公路普查等，但是经常会遇到这样的问题:由于早期的公路建设和管理不规范,许多道路的线形资料已经遗失或部分遗失，甚至有些低等级的道路根本没有线形资料,再加上道路的改建扩建等情况,导致许多道路线形资料不全,或者与实际情况不符,这给科学研究带来不少麻烦。传统的测量方法一般采用经纬仪测设平面线形,用水准仪测设高程，这种方法最大的缺点是工作速度慢，强度大，尤其对于路网的测量更显力不从心。gps在这方面具有明显的优势。gps的定位方法有静态定位和动态定位，前者包括伪距法、载波相位测量法和射电干涉测量法,后者包括单动态定位法、伪距差分动态定位和差分动态载波相位测量。在公路路线测量中,根据研究需求，可以采用单机低精度测量方式，也可采用gps动态定位中的差分动态载波相位测量。该测量方法的基本原理是:在接收机的振荡器中产生一个和初相与卫星载波信号完全相同的基准信号,根据某瞬间接收机产生的基准信号的相位和接收到的来自卫星的载波信号的相位差可以求出该瞬间从卫星到接收机的距离。但是在低精度测量中，采样点距离的计算由于难以准确获得地球椭球半径，且由于采样频率较低(1～2hz)，难以准确获得测量桩号，并且由于测得的采样点原始为经纬度、高程数据，无法直接获得测量公路的平纵参数，一般仅靠人工估算，给后续研究带来困难。

关于本发明中所用概念的说明如下：

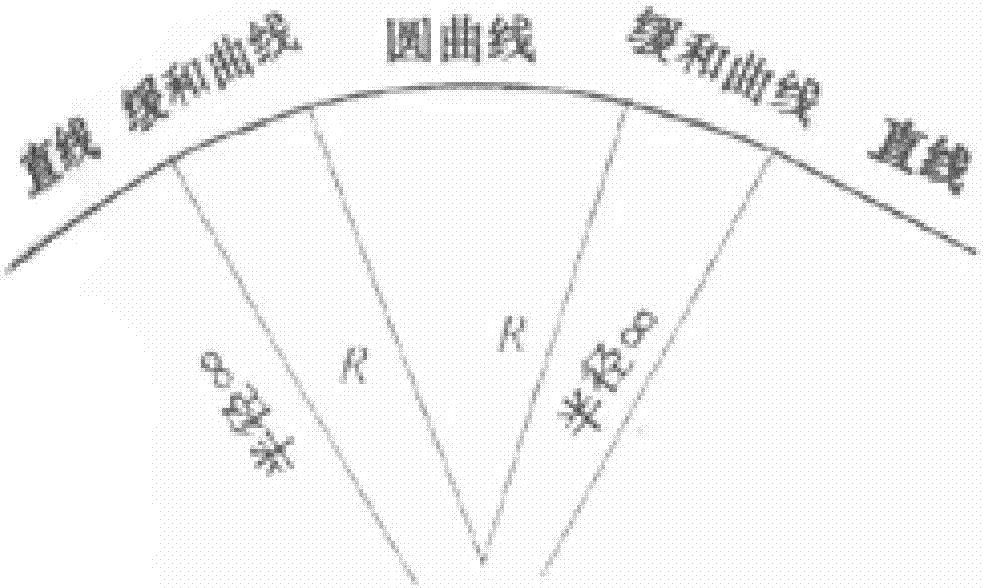
公路路段包括平曲线与纵面段，平曲线由直线段、缓和曲线和圆曲线组成，缓和曲线位于直线段和圆曲线之间；纵面段包括单一纵坡段和竖曲线。

技术实现要素：

针对现有技术中存在的不足，本发明的目的在于提供一种能够连续测量公路线形的方法，它可以克服传统测量方法测量速度慢、效率低的缺点，可以在准确获得公路桩号的同时，获得公路的平曲线中直线、缓和曲线、圆曲线的起始点桩号和参数以及纵断面中单一纵坡段和竖曲线的起始点桩号和参数。

1.一种基于gps的车载公路线形测量方法，该方法利用行驶在公路上的测量车来测量公路线形，其特征在于，包括以下步骤：

步骤1，设测量车的行驶起点桩号为a，测量车的行驶终点桩号为b；利用安装在测量车上的gps接收机采集桩号a至桩号b之间的所有gps信号；

所述gps信号包括n个采样点中每个采样点的经度、纬度、高程；n为大于等于1的自然数；

步骤2，以桩号a处为原点，经度为x轴，纬度为y轴建立平面坐标系；

步骤21，任选一采样点作为当前采样点i，则该当前采样点的下一采样点为i+1，所述当前采样点i的坐标为(xi，yi)，采样点i+1的坐标为(xi+1,yi+1),计算采样点i到采样点i+1间的斜率si；其中，i＝1，2，…，n；n为大于等于1的自然数；

若si大于阈值ε1，则采样点i到采样点i+1之间的公路段为平曲线中的直线段，执行步骤22；否则，执行步骤3；

步骤22，重复步骤21，直至所有采样点都作为当前采样点i，得到平曲线中的k个直线段，k为大于等于2的正整数；

步骤23，设平曲线中k个直线段的任一直线段p两端点的采样点分别为采样点m和采样点n，且m＞n，则采样点n为平曲线中直线段p的起点，采样点m为平曲线中直线段p的终点；其中，m＝1,2，…，n，n＝1,2，…，n，p＝1,2，…k；

步骤24，重复步骤23，直至得到平曲线中所有直线段的起点坐标和终点坐标；

步骤25，设n个采样点中的任一采样点j的坐标为(xj，yj)；j＝1，2，…，n；

设平曲线直线段的方程为：

y＝a1x+b1

则误差方程为：dtj＝a1xj+b1-yj；

其中，a1，b1为平曲线中直线段方程的参数；

步骤26，通过式(1)、式(2)，得到平曲线中直线段方程的参数a1，b1：

其中，[]表示

步骤3，设平曲线中圆曲线的方程为：

(x-a)²+(y-b)²＝r²(3)

其中，a，b为平曲线中圆曲线的圆心坐标，r为平曲线中圆曲线的半径；

步骤31，将采样点j的坐标带入式(3)得到误差方程dtj：

步骤32，对误差方程dtj根据等精度观测和最小二乘法则，通过式(5)、式(6)、式(7)得到平曲线中圆曲线的圆心坐标(a，b)和平曲线中圆曲线的半径r；

其中，rj'表示采样点j处对应的圆曲线半径；[]表示

步骤33，从步骤24得到的平曲线中所有直线段中任取两相邻的直线段，获取该两相邻直线段间的采样点的中点，设该两相邻直线段间的采样点数为c；

步骤331，以该中点为中心取c/2个中点前的采样点和c/2个中点后的采样点，组成c个采样点；

步骤332，设步骤33中的c个采样点中的任一采样点d的坐标为(xd，yd)；d＝1，2，…，c；

设通过c个采样点拟合成的拟合圆曲线方程为：

(x-a′)²+(y-b′)²＝rc²(8)

其中，a′，b′为拟合圆曲线的圆心坐标；rc为拟合圆曲线的半径；

将采样点d的坐标带入式(8)得到误差方程dtd：

步骤333，对误差方程dtd根据等精度观测和最小二乘法则，通过式(10)、式(11)、式(12)得到rc；

步骤334，若(rc-r)＞ε2，执行步骤335；否则，c个采样点属于平曲线中的圆曲线；

步骤335，c＝c-1,重复步骤331至步骤334，直至c个采样点属于平曲线中的圆曲线，取c个采样点中两端的两个采样点作为圆曲线的起点和终点；

步骤34，重复步骤33，直至找到平曲线中所有相邻直线段间的圆曲线的起点和终点；

步骤35，平曲线中直线段和圆曲线之间的采样点属于缓和曲线，直线段和圆曲线之间的采样点的两端的采样点即为缓和曲线的起点和终点；

进一步地，还包括：

步骤4，以桩号a处为原点，经度为x轴，高程为z轴建立纵面坐标系；

步骤41，从n个采样点中任选一采样点作为当前采样点v，则该当前采样点的下一采样点为v+1，所述当前采样点v的坐标为(xv，zv)，采样点v+1的坐标为(xv+1,zv+1),计算当前采样点v到采样点v+1间的坡度sv；其中，v＝1，2，…，n；n为大于等于1的自然数；

若sv小于等于阈值ε3，则采样点v到采样点v+1之间的公路段为纵坡段，执行步骤42；否则执行步骤5；

步骤42，重复步骤41，直至所有采样点都作为当前采样点v，得到s个纵坡段，s为大于等于2的正整数；

步骤43，设s个纵坡段中的任一纵坡段q两端点的采样点分别为采样点r和采样点t，且r＞t，则采样点t为纵坡段q的起点，采样点r为纵坡段q的终点；其中，r＝1,2，…，n，t＝1,2，…，n，q＝1,2，…s；

步骤44，重复步骤43，直至得到所有纵坡段的起点坐标和终点坐标；

步骤45，纵坡段起点和终点之间的所有采样点都属于竖曲线，竖曲线两端的采样点即为竖曲线的起点和终点；

步骤5，设n个采样点中的任一采样点l的坐标为(xl,zl)；l＝1，2，…，n；

设竖曲线的方程为：

z＝ex²+fx+g(13)

其中，e，f，g为竖曲线的参数；

步骤51，通过式(14)得到竖曲线的参数e，f，g：

步骤52，通过式(15)得到竖曲线半径ra：

式(15)中，z"为对z求二次导数，z′为对z求一次导数。

进一步地，还包括：

步骤61，通过式(16)得到测量车测量起点a到测量车测量终点b之间的距离d：

式(16)中：

其中，xa，ya，za分别为a点的经度、纬度和高程；xb，yb，zb分别为b点的经度、纬度和高程；

步骤62，以每100m为间隔将距离d按照*km+*m的格式输出公路里程数组d[num1][num2]。

与现有技术相比，本发明具有以下技术效果：

本发明将gps信号运用到测量公路线形中，测量速度快、效率高，并且在准确获得公路桩号的同时，获得公路的平曲线中直线段、缓和曲线、圆曲线的起始点桩号和参数及纵断面中单一纵坡和竖曲线的起始点桩号和参数。

附图说明

图1为平曲线路段示意图；

图2为竖曲线示意图；

图3为绘制的实验路段的平曲线图；

图4为绘制的实验路段的竖曲线图。

具体实施方式

下面通过附图和实施例对本发明作进一步说明。

实施例1

本实施例提供了一种基于gps的车载公路线形测量方法，该方法利用行驶在公路上的测量车来测量公路线形，包括以下步骤：