一种数据驱动的伺服系统最优控制方法与流程

本发明涉及直流电机伺服控制系统，属于机电控制技术领域，具体涉及一种数据驱动的伺服系统最优控制方法。

背景技术：

在伺服系统控制中，由于动态摩擦、负载变化和外部干扰等不确定性因素的存在，系统模型会发生改变。此外，如果控制系统中存在未知参数，对这些参数的初始估计值可能与其真实值相差较大。因此，如果在控制过程中不能准确得到系统模型，就需要研究一种不依赖于系统模型的控制算法。

数据驱动的控制算法直接利用采样数据替代系统模型来设计控制器，其中数据驱动的自适应动态规划算法是一种有效的最优控制方法。数据驱动的自适应动态规划理论融合了dp、rl以及函数近似等方法,本质就是利用在线或离线数据,采用函数近似结构来估计系统性能指标函数,然后依据最优性原理来获得最优的控制策略。

技术实现要素：

有鉴于此，针对伺服系统不能精确建模问题，本发明采用一种数据驱动的伺服系统最优控制方法，该方法不需要知道具体的系统模型，只需要状态误差量可测。

本发明的设计思路为：

设直流电机伺服系统误差方程为：

其中，u为控制量，e为状态误差；

定义代价函数如下：

其中，r(e,u)＝q(e)+u^tru，q是正定的，r为正定对称矩阵；

最终控制状态误差e在代价函数最优的条件下收敛到0，利用得到的控制量u对伺服系统进行控制。

实现本发明的技术方案如下：

一种数据驱动的伺服系统最优控制方法，包括数据驱动的状态误差反馈控制和数据驱动的自适应优化控制两部分：

第一部分：数据驱动的状态误差反馈控制

101、设置k＝1，初始化第k-1、k时刻的系统反馈增益k(k-1)、k(k)；

102在时间区间[kt,(k+1)t]上，将顺序应用所述系统反馈增益k(k-1)和k(k)于伺服系统；

103、采样伺服系统的状态误差，并按照式(10)、(12)到(15)计算状态误差关系矩阵a(k)，ge(k)和gu(k)；

a(k)＝a0(k)a1(k)(10)

a1(k)＝e((k+1/2)t)(e(kt))⁺(12)

a0(k)＝e((k+1)t)(e((k+1/2)t))⁺(13)

然后可得：

gu(k)＝(a0(k)-a1(k))(k(k)-k(k-1))⁺(14)

ge(k)＝a0(k)-gu(k)·k(k)(15)

其中，e(kt)、e((k+1/2)t)表示第k、(k+1/2)时刻系统状态误差，符号·⁺代表矩阵的伪逆；

104、按照式(11)计算k(k+1)和k(k+2)；

其中，λ表示设定步长，为0-1之间的常数；符号||||表示矩阵的frobenius范数。

105、判断k是否小于设定阈值，即第k时刻是否已经到达了设定的截止时间t1，若是进入第二部分，否则令k＝k+1，返回到步骤102；

在第一部分中，状态误差反馈控制量在应用的同时不断调整，获得的输入u⁰和状态误差数据e可以用于下一部分的自适应优化控制器。

第二部分：数据驱动的自适应优化控制

设置j＝0，定义φki、u^j，的表达式如下

φki＝φi(e(tk))-φi(e(tk-1))

其中j为迭代次数；φi(e),(i＝1,...nw)，ψi(e,u),(i＝1,...nc)，σi(e),(i＝1,...nl)为基函数；为权值，u⁰为状态误差反馈控制量，为u^j(e)的估计值，为函数u^j(e)实际值与估计值之间的逼近误差。

201、基于第一部分中得到的系统状态误差，计算φki和然后获取

202、基于步骤201中获取的通过式(22)计算权值

其中m为正整数。

通过式(23)计算权值

其中l为权值的任意可能值；

203、判断是否成立，若是，进入步骤204，否则令j＝j+1，返回到步骤201，ε为给定阈值；

204、为最优控制量的近似值，之后实时利用其对伺服系统进行控制。

有益效果

该方法包括状态误差反馈控制和基于策略迭代的自适应优化控制，其中状态误差反馈控制可以利用采样数据实时计算反馈增益k；自适应优化控制器直接使用状态误差反馈控制所得的控制量和状态误差量进行迭代计算逐渐逼近到最优控制量；该方法不需要知道具体的系统模型，只需要状态误差量可测。

附图说明

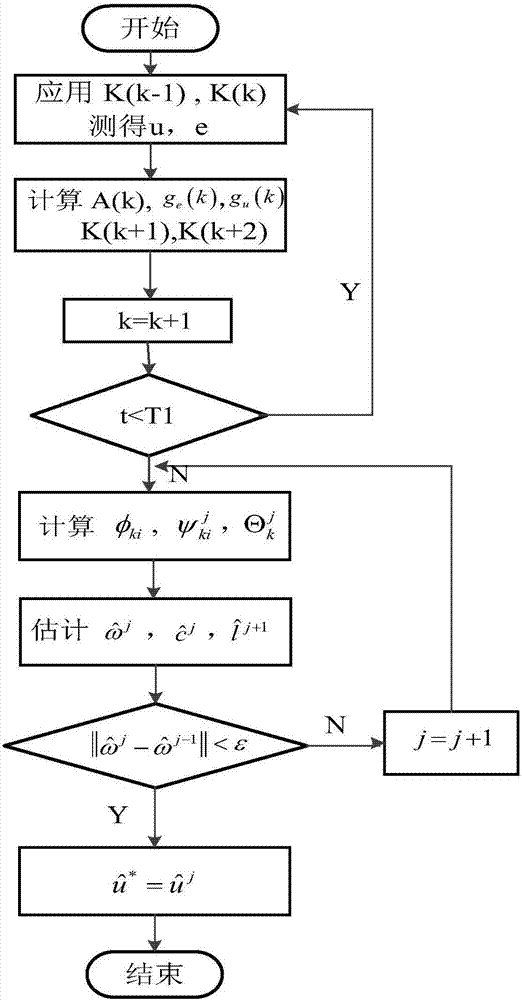
图1为数据驱动的伺服系统最优控制方法流程图。

图2为初始反馈增益调整图。

图3为matlab仿真代价函数对比图。

图4为matlab仿真状态轨迹对比图。

图5为计算完成后将两个控制量实时应用于系统所得的matlab仿真状态轨迹对比图。

具体实施方式

下面结合附图和具体实例对本发明进行详细说明。

某直流电机伺服系统的数学模型可写作:

其中，x(t)＝[x1(t),x2(t)]^t分别是电动机输出角位置、转子角速度，该状态量是可测的；u为控制量；f(x,u)是未知的，满足f(0,0)＝0。

本发明设计最优控制方法使得电机伺服系统达到期望状态xd＝[x1d,0]^t，即跟踪阶跃信号，且此时ud＝0。状态误差定义为：e＝x-xd且e0＝x0-xd。误差系统方程为：

本发明最终控制状态误差收敛到0。

针对最优控制，需要定义代价函数如下：

其中r(e,u)＝q(e)+u^tru，q是正定的，r为正定对称矩阵。对于该代价函数作如下假设：

假设1：代价函数(3)取值与控制量u有关，对于每个e0有唯一极小值。

假设2：代价函数(3)对于任意分段连续的控制输入u满足

数据驱动的伺服系统最优控制系统结构如图1所示，由状态误差反馈控制器和自适应优化控制器两部分组成，下面分别进行具体阐述。

1.状态误差反馈控制器。

对于未知伺服系统，系统信息都隐含在状态误差和输入信息中,通过系统信息采样可以建立以下数据关系式：

e((k+1)t)＝g(e(kt),u(kt))(4)

其中g(e,u)是未知的，k＝0,1,2...，t是采样周期，省略t可以将式(4)简化为：

e(k+1)＝g(e(k),u(k))(5)

该方程包含状态误差和输入信号，揭示了系统(2)的内部特征，可以直接用来搜索合适的反馈控制量。鉴于系统(2)和系统(4)代表同一个系统，可以得到g(0,0)＝0。

为了使状态误差达到0，对式(5)在任意点e(k)和0点应用拉格朗日均值定理，可以得到：

e(k+1)＝ge(k)e(k)+gu(k)u(k)(6)

其中0＜θ＜1。对此，作如下假设：

假设3：对于任意k∈n，在每个时间区间[kt,(k+1)t]上，矩阵gu(k)和ge(k)保持不变。

为保证该假设成立，应该选取足够小的采样周期t。

将时间区间[kt,(k+1)t]分成两部分，在第一部分[kt,(k+1/2)t]，应用反馈增益k(k-1)，在第二部分应用反馈增益k(k)，即设计状态误差反馈控制量为：

根据假设3和式(6)，可以得到状态误差关系式如下：

e((k+1/2)t)＝[ge(k)vgu(k)k(k-1)]e(kt)＝a1(k)e(kt)(8)

e((k+1)t)＝[ge(k)+gu(k)k(k)]e((k+1/2)t)＝a0(k)e((k+1/2)t)(9)

因此可得：

e(k+1)＝a0(k)a1(k)e(k)＝a(k)e(k)(10)

明显可知，通过调节a(k)可以使得状态误差e收敛到0，通过调节反馈增益k(k)可以调节a(k)，定义k(k)调节率如下：

其中λ是步长，0＜λ＜1，应该选取较小值保证e收敛，但不能太小以保证搜索效率；符号||·||代表frobenius范数；符号·+代表矩阵的伪逆。当||a(k)||≥1时，反馈增益k始终按照式(11)不断调节，其中所需要的实时矩阵gu(k)和ge(k)可用如下方法求取。

状态误差关系矩阵a1(k)和a0(k)可以用测得的状态误差通过式(8)和(9)求得：

a1(k)＝e((k+1/2)t)(e(kt))⁺(12)

a0(k)＝e((k+1)t)(e((k+1/2)t))⁺(13)

然后可得：

gu(k)＝(a0(k)-a1(k))(k(k)-k(k-1))⁺(14)

ge(k)＝a0(k)-gu(k)·k(k)(15)

当||a(k)||≥1时，反馈增益k(k)根据式(11)到(15)不断实时更新；当||a(k)||＜1时，k保持不变。在该过程中，状态误差反馈控制量在应用的同时不断调整，获得的输入u⁰和状态误差数据e可以用于下一部分的自适应优化控制器。

2.自适应优化控制器。

采用上一过程中产生的数据，该部分自适应优化控制器采用自适应动态规划策略迭代的方法来解决伺服系统最优控制问题。

针对上述状态误差系统，基本的策略迭代方法如下：

(1)从下式中求解v^j(e(t))：

r(e，u^j(e))+(ve^j(e))^t(f(e，u^j(e)))＝0，v^j(0)＝0(16)

其中j是迭代次数。

(2)通过下式计算控制量：

选择时间序列tk,k＝0,1,...，满足0＜t1＜t2＜...＜tm＜∞，其中m为足够大的整数。由代价函数定义(3)可知：

可以转化为：

下面用下列函数结构逼近上式中未知的v^j(e)，和u^j(e)，分别表示为：

其中为权值；φi(e),(i＝1,...nw)，ψi(e,u),(i＝1,...nc)，σi(e),(i＝1,...nl)为基函数；分别为用函数结构逼近三个函数v^j(e)，和u^j(e)的逼近误差。故式(18)可以写作：

其中是逼近误差；

方便起见，做如下定义：

φki＝φi(e(tk))-φi(e(tk-1))

则(19)可以简写为：

不失一般性，作如下假设：

假设4：对于所有的u^j，存在和γ＞0，使得对于所有的下列不等式成立：

故根据式(20)可以通过下式求解权值矩阵：

根据式(17)，可以求解得到权值

利用已有采样数据，通过式(22)和(23)不断迭代计算，当t、nw、nc和nl都趋近于无穷时，权值收敛的各自的最优值，即各未知函数收敛到其最优值。

综上所述，数据驱动的伺服系统最优控制方法如下：

第一部分：数据驱动的状态误差反馈控制

101、设置k＝1，初始化第k-1、k时刻的系统反馈增益k(k-1)、k(k)；

102在时间区间[kt,(k+1)t]上，将顺序应用所述系统反馈增益k(k-1)和k(k)于伺服系统；

103、采样伺服系统的状态误差，并按照式(10)、(12)到(15)计算状态误差关系矩阵a(k)，ge(k)和gu(k)；

a(k)＝a0(k)a1(k)(10)

a1(k)＝e((k+1/2)t)(e(kt))⁺(12)

a0(k)＝e((k+1)t)(e((k+1/2)t))⁺(13)

然后可得：

gu(k)＝(a0(k)-a1(k))(k(k)-k(k-1))⁺(14)

ge(k)＝a0(k)-gu(k)·k(k)(15)

其中，e(kt)、e((k+1/2)t)表示第k、(k+1/2)时刻系统状态误差，符号·⁺代表矩阵的伪逆；

104、按照式(11)计算k(k+1)和k(k+2)；

其中，λ表示设定步长，为0-1之间的常数

105、判断k是否小于设定阈值，即第k时刻是否已经到达了设定的截止时间t1，若是进入第二部分，否则令k＝k+1，返回到步骤102。

执行完第一部分得到一系列系统状态误差e(kt)、e((k+1/2)t)和系统反馈控制输入u⁰用于下一部分的自适应优化控制器。

第二部分：数据驱动的自适应优化控制

设置j＝0，定义φki、u^j，的表达式如下

φki＝φi(e(tk))-φi(e(tk-1))

其中j为迭代次数；φi(e),(i＝1,...nw)，ψi(e,u),(i＝1,...nc)，σi(e),(i＝1,...nl)为基函数；为权值；为u^j(e)的估计值,为函数u^j(e)实际值与估计值之间的逼近误差。

201、基于第一部分中得到的系统状态误差，计算φki和然后获取

202、基于步骤201中获取的通过式(22)计算权值

其中m为正整数。

通过式(23)计算权值

其中l为权值的任意可能值。

203、判断是否成立，若是，进入步骤204，否则令j＝j+1，返回到步骤201；每次返回时，将本次循环202中计算得到的带入下次循环步骤201中计算，ε为给定阈值。

204、为最优控制量的近似值，之后实时利用其对伺服系统进行控制。

整个过程的流程图如图2所示。

利用matlab对上述方法进行仿真。考虑具有以下二阶模型的电机伺服系统：

系统的模型参数设置为：θ1＝-2,θ2＝-5,θ3＝1,θ4＝0andks＝900。

代价函数定义为：

系统初始值设置为：x0＝[-10]^t，k(0)＝[-10]，k(1)＝[0-1]。

第一部分采用状态误差反馈控制器，该阶段设置为1.5s。图3表示的即该过程中反馈增益k的调整图线。

第二部分采用自适应优化控制器，直接利用第一部分获得的数据，使用多项式基函数，经过17次迭代之后，获得最终的近似最优控制量。图4表示初始控制量(第一部分所得)和近似最优控制量所对应的代价函数对比图，明显可以看出近似最优控制量的代价函数较小。图5为计算完成后实时将两个控制量应用于系统所得的状态轨迹对比图，明显可以看出应用近似最优控制量系统收敛速度更快。

综上所述，以上仅为本发明的较佳实施例而已，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。