一类奇异时滞系统的渐近稳定性判别方法、维持方法与流程

本发明涉及自动控制技术领域，尤其涉及一类奇异时滞系统的渐近稳定性判别方法以及该类奇异时滞系统的渐近稳定性维持方法。

背景技术：

在各类物理、生物和工业系统中时滞现象是普遍存在的，时滞的存在使得系统分析和综合变得更加复杂,同时时滞的存在也是系统不稳定和系统性能变差的重要原因。奇异系统是一类比正常系统更具广泛形式的动力系统，比正常系统能更好地描述物理系统,奇异系统模型广泛存在于社会生产的各个领域中，如：电力系统、经济系统、机器人系统、宇航工程和生物系统。因此，奇异时滞系统在关于控制问题的数学模型中有重要作用。

根据依赖于时滞的大小可以把奇异时滞系统的稳定条件分成两类，不包含时滞信息的系统称为时滞独立系统，包含时滞信息的系统称为时滞依赖系统。

现有技术中奇异时滞系统的时滞独立稳定性已被广泛研究，例如：使用特征函数方法，对时滞独立稳定性的条件进行了讨论。

本申请人发现：现有技术至少存在以下技术问题：

现有技术中奇异时滞依赖系统的稳定性无法完全描述，由此无法准确地判断奇异时滞依赖系统的稳定性，也无法有效地提高奇异时滞依赖系统的稳定性。

技术实现要素：

本发明的至少一个目的是提出一类奇异时滞系统的渐近稳定性判别方法以及该类奇异时滞系统的渐近稳定性维持方法，解决了现有技术存在无法全面的描述该类奇异时滞依赖系统的稳定性的技术问题。

为实现上述目的，本发明提供了以下技术方案：

本发明实施例提供的一类奇异时滞系统的渐近稳定性判别方法，包括以下步骤:

步骤a、利用数学分解方法对一类奇异时滞系统的时滞稳定性进行分析，以得出维持该类奇异时滞依赖系统稳定性的条件；

步骤b、依据所述维持一类奇异时滞依赖系统稳定性的条件，判别所述奇异时滞依赖系统的稳定性。

优选地，所述数学分解方法为schur分解方法。

优选地，所述条件为充分必要条件。

优选地，所述一类奇异时滞系统为线性时滞系统。

优选地，所述步骤a，包括以下步骤：

步骤a1、得到非奇异时滞系统的稳定的条件；

步骤a2、将非奇异时滞系统的稳定的条件与schur分解方法相结合来分析一类奇异时滞系统的时滞稳定性，以得出维持该类奇异时滞依赖系统稳定性的条件。

优选地，所述步骤a2，包括以下步骤:

步骤a21：假设条件det(σe-a)≠0成立，矩阵(δe-a)^-1存在，系统其中e,a∈r^n×n，δ∈c，e为奇异矩阵；两边都左乘(δe-a)^-1，于是得到式子；

步骤a22：因为矩阵(δe-a)^-1存在，令证明故有因此将式子改写成

步骤a23：因为为方阵，存在酉矩阵u使得成立；其中t是一个上三角矩阵，它的对角元素是的特征值；选取适当的u阵使得t前m个对角元素都是非零的特征值α1,α2,…,αm，而剩余的对角线元素是零特征值αm+1,αm+2,…,αn；

步骤a24：令x(t)＝uz(t)则，

写成的形式；

步骤a25：令z(t)＝[z1(t),....,zm(t),zm+1(t),....zn(t)]^t系统的最后一个标量方程仅包含一个变量zn(t)，第n个方程是并得一致性条件zn(t)≡0,t≥-τ；

步骤a26：令zn(t)≡0,t≥-τ，在第n-1个方程中有显然zn-1(t)≡0,t≥-τ是成立的；现在已证得标量元素zn(t)≡zn-1(t)≡0,t≥-τ，同理也证得zk(t)≡0,t≥-τ,k＝m+1,m+2,...,n.

步骤a27：在系统中，对于k＝m+1,m+2,....n；令zk(t)＝0得到一个m维的系统其中r的对角元素α1,α2,…,αm都不为零，并且有亦有[zm+1(t),....,zn(t)]^t＝0；

步骤a28：因为矩阵r是非奇异的，系统化为一个时滞系统，当且仅当它的特征方程的所有特征根都在左半平面上时，该系统是渐近稳定的；

当且仅当m个标量方程是渐近稳定的，系统的所有特征根位于左半平面；

步骤a29：有式子x(t)＝uz(t)＝u[z1(t),...,zm(t),0...,0]^t并且矩阵u是非奇异的，系统是渐近稳定的等价于系统是渐近稳定的等价于式中m个标量方程渐近稳定

。

优选地，所述步骤b，具体为：

若条件det(σe-a)≠0成立，其中：e,a∈r^n×n，δ∈c；令ak≠0，k＝1,2,...,m，ak＝0，k＝m+1,m+2,...,n，并且其中uk,vk∈r；定义αk＝λk(eδ)；当且仅当对于所有的ak≠0，k＝1,2,...,m，有条件成立时，判定系统是渐近稳定的。

优选地，所述奇异时滞系统为奇异时滞依赖系统。

本发明实施例提供的一类奇异时滞系统的渐近稳定性维持方法，包括以下步骤：

根据本发明任一技术方案提供的一类奇异时滞系统的渐近稳定性判别方法判别一类奇异时滞系统的渐近稳定性；

利用所述维持一类奇异时滞依赖系统稳定性的条件，以提高奇异时滞系统的渐近稳定性。

基于上述技术方案，本发明实施例至少可以产生如下技术效果：

本发明可以利用数学分解方法对一类奇异时滞系统的时滞稳定性进行分析，以得出维持该类奇异时滞依赖系统稳定性的条件，由此全面地描述了该类奇异时滞依赖系统的稳定性(本发明优选方案中使用schur分解方法对线性时滞系统的时滞稳定性进行分析，给出了一类奇异时滞依赖系统的充分必要条件，结果表明该判别方法能完全描述该类奇异时滞依赖系统稳定性)，然后依据维持该类奇异时滞依赖系统稳定性的条件，判别该类奇异时滞依赖系统的稳定性，解决了现有技术存在无法全面的描述该类奇异时滞依赖系统的稳定性的技术问题。

附图说明

此处所说明的附图用来提供对本发明的进一步理解，构成本申请的一部分，本发明的示意性实施例及其说明用于解释本发明，并不构成对本发明的不当限定。在附图中：

图1为本发明实施例所提供的一类奇异时滞系统的渐近稳定性判别方法的主要流程的示意图；

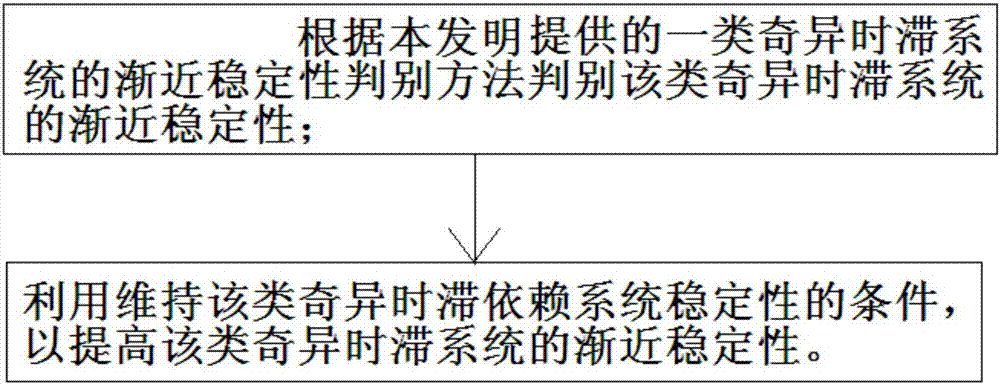
图2为应用本发明实施例所提供的一类奇异时滞系统的渐近稳定性判别方法的该类奇异时滞系统的渐近稳定性维持方法的主要流程的示意图。

具体实施方式

下面可以参照附图图1～图2以及文字内容理解本发明的内容以及本发明与现有技术之间的区别点。下文通过附图以及列举本发明的一些可选实施例的方式，对本发明的技术方案(包括优选技术方案)做进一步的详细描述。需要说明的是：本实施例中的任何技术特征、任何技术方案均是多种可选的技术特征或可选的技术方案中的一种或几种，为了描述简洁的需要本文件中无法穷举本发明的所有可替代的技术特征以及可替代的技术方案，也不便于每个技术特征的实施方式均强调其为可选的多种实施方式之一，所以本领域技术人员应该知晓：可以将本发明提供的任一技术手段进行替换或将本发明提供的任意两个或更多个技术手段或技术特征互相进行组合而得到新的技术方案。本实施例内的任何技术特征以及任何技术方案均不限制本发明的保护范围，本发明的保护范围应该包括本领域技术人员不付出创造性劳动所能想到的任何替代技术方案以及本领域技术人员将本发明提供的任意两个或更多个技术手段或技术特征互相进行组合而得到的新的技术方案。

本发明实施例提供了一种可以简单、全面地描述一类奇异时滞依赖系统的稳定性，进而可以有效地提高该类奇异时滞依赖系统的稳定性的奇异时滞系统的渐近稳定性判别方法以及该类奇异时滞系统的渐近稳定性维持方法。本发明基于线性时滞系统的稳定性判别方法，使用schur分解的方法给出了一类奇异时滞系统的渐近稳定性的判别方法，该类奇异时滞系统的稳定性可以被完全描述。

下面结合图1～图2对本发明提供的技术方案进行更为详细的阐述。

如图1所示，本发明实施例所提供的奇异时滞系统的渐近稳定性判别方法，包括以下步骤:

步骤a、利用数学分解方法对奇异时滞系统的时滞稳定性进行分析，以得出维持一类奇异时滞依赖系统稳定性的条件；

步骤b、依据维持一类奇异时滞依赖系统稳定性的条件，判别该类奇异时滞依赖系统的稳定性。

本发明可以利用数学分解方法对一类奇异时滞系统的时滞稳定性进行分析，以得出维持该类奇异时滞依赖系统稳定性的条件，由此全面地描述了该类奇异时滞依赖系统的稳定性(本发明优选方案中使用schur分解方法对线性时滞系统的时滞稳定性进行分析，给出了一类奇异时滞依赖系统的充分必要条件，结果表明该判别方法能完全描述该类奇异时滞依赖系统稳定性)，然后依据维持该类奇异时滞依赖系统稳定性的条件，判别该类奇异时滞依赖系统的稳定性。

作为可选地实施方式，数学分解方法为schur分解方法。schur分解是应用schur定理(或称：舒尔定理)进行分解的数学方法。

作为可选地实施方式，条件为充分必要条件。必要条件越全面、越充分，则对一类奇异时滞依赖系统的稳定性的描述越全面准确。

作为可选地实施方式，一类奇异时滞系统为线性时滞系统。线性时滞系统更便于采用数学分解方法进行分析。

作为可选地实施方式，步骤a，包括以下步骤：

步骤a1、得到非奇异时滞系统的稳定的条件(结论)；

步骤a2、将非奇异时滞系统的稳定的条件与schur分解方法相结合来分析一类奇异时滞系统的时滞稳定性，以得出维持该类奇异时滞依赖系统稳定性的条件。

作为可选地实施方式，奇异时滞系统为奇异时滞依赖系统。奇异时滞依赖系统包含时滞信息，其稳定性更具有研究价值。

作为可选地实施方式，步骤a2，包括以下步骤:

步骤a21：假设条件det(σe-a)≠0成立，矩阵(δe-a)^-1存在，系统其中e,a∈r^n×n，δ∈c，e为奇异矩阵；两边都左乘(δe-a)^-1，于是得到式子；

步骤a22：因为矩阵(δe-a)^-1存在，令得出(可以证明)并得出因此将式子改写成

步骤a23：因为为方阵，存在酉矩阵u使得成立；其中t是一个上三角矩阵，它的对角元素是的特征值；选取适当的u阵使得t前m个对角元素都是非零的特征值α1,α2,…,αm，而剩余的对角线元素是零特征值αm+1,αm+2,…,αn；

步骤a24：令x(t)＝uz(t)，则写成的形式；

步骤a25：令z(t)＝[z1(t),....,zm(t),zm+1(t),....zn(t)]^t系统的最后一个标量方程仅包含一个变量zn(t)，第n个方程是并得一致性条件zn(t)≡0,t≥-τ；

步骤a26：令zn(t)≡0,t≥-τ，在第n-1个方程中有显然zn-1(t)≡0,t≥-τ是成立的；现在已证得标量元素zn(t)≡zn-1(t)≡0,t≥-τ，同理也证得zk(t)≡0,t≥-τ,k＝m+1,m+2,...,n.

步骤a27：在系统中，对于k＝m+1,m+2,....n；令zk(t)＝0得到一个m维的系统其中r的对角元素α1,α2,…,αm都不为零，并且有亦有[zm+1(t),....,zn(t)]^t＝0；

步骤a28：因为矩阵r是非奇异的，系统化为一个时滞系统，当且仅当它的特征方程的所有特征根都在左半平面上时，该系统是渐近稳定的；

当且仅当m个标量方程是渐近稳定的，系统的所有特征根位于左半平面；

步骤a29：有式子x(t)＝uz(t)＝u[z1(t),...,zm(t),0...,0]^t并且矩阵u是非奇异的，系统是渐近稳定的等价于系统是渐近稳定的等价于式中m个标量方程渐近稳定。

下面更为详细地说明本发明步骤a2：

步骤a21：如果对于任意的ε＞0，存在δ＝δ(ε)＞0即所有连续函数满足一致性条件并且有对于所有的t≥0，系统的初值问题的解满足则奇异时滞系统的平凡解是稳定的。如果系统是稳定的并且满足则它的平凡解是渐近稳定的。

步骤a22：e,a∈r^n×n，δ∈c。假设条件det(σe-a)≠0成立，故矩阵(δe-a)^-1存在。系统其中矩阵e是奇异的，两边都左乘(δe-a)^-1，于是得到式子。

因为矩阵(δe-a)^-1存在，令可以证明故有

因此式子可以改写成

步骤a23：如果f∈c^n×n，那么存在酉矩阵u∈c^n×n,有u^hfu＝t。其中t∈c^n×n是上三角矩阵，可以选择适当的u使得f的特征值出现在对角元素上的任意位置。

为方阵，所以存在酉矩阵u使得成立。其中t是一个上三角矩阵，它的对角元素是的特征值。选取适当的u阵使得t前面的m个对角元素都是非零的特征值α1,α2,…,αm，而剩余的对角线元素是零特征值αm+1,αm+2,…,αn。

步骤a24：令x(t)＝uz(t),其中u为酉矩阵，有u^hu＝i，则可以写成的形式；

步骤a25：令z(t)＝[z1(t),....,zm(t),zm+1(t),....zn(t)]^t系统的最后一个标量方程仅包含一个变量zn(t)，第n个方程是并可得一致性条件zn(t)≡0,t≥-τ。

步骤a26：令zn(t)≡0,t≥-τ，在第n-1个方程中有显然zn-1(t)≡0,t≥-τ是成立的。现证得标量元素zn(t)≡zn-1(t)≡0,t≥-τ，同理也可证得zk(t)≡0,t≥-τ,k＝m+1,m+2,...,n.

步骤a27：在系统中，对于k＝m+1,m+2,....n。令zk(t)＝0可以得到一个m维的系统其中r的对角元素α1,α2,…,αm都不为零，并且有亦有[zm+1(t),....,zn(t)]^t＝0。

步骤a28：因为矩阵r是非奇异的，系统可化为一个时滞系统，当且仅当它的特征方程的所有特征根都在左半平面上时，该系统是渐近稳定的。

当且仅当m个标量方程是渐近稳定的，系统的所有特征根位于左半平面。

步骤a29：有x(t)＝uz(t)

，和[zm+1(t),....,zn(t)]^t＝0，故可得x(t)＝uz(t)＝u[z1(t),...,zm(t),0...,0]^t。因为矩阵u是非奇异的，故系统是渐近稳定的等价于系统是渐近稳定的同样等价于式中m个标量方程渐近稳定。

作为可选地实施方式，步骤b，具体为：

若条件det(σe-a)≠0成立，其中：e,a∈r^n×n，δ∈c；令ak≠0，k＝1,2,...,m，ak＝0，k＝m+1,m+2,...,n，并且其中uk,vk∈r；定义αk＝λk(eδ)；当且仅当对于所有的ak≠0，k＝1,2,...,m，有条件成立时，判定系统是渐近稳定的。

下面更为详细地说明本发明步骤b即奇异时滞系统稳定性的判别的简单方法：

步骤b1：系统的稳定性由m个标量微分方程决定，其中αk＝λk(eδ),βk＝δλk(eδ)-1。

因为ak≠0，k＝1,2,...,m，系统可以改写成即为

步骤b2：矩阵a的特征值可以表示成λk(a)＝ak+ibk，其中ak,bk∈r,对于k＝1,2,...,n，当且仅当对于所有特征值λk(a),条件成立时，时滞系统是渐近稳定的。

步骤b3：是一个时滞微分方程。e,a∈r^n×n。假设条件det(σe-a)≠0成立，令ak≠0，k＝1,2,...,m，ak＝0，k＝m+1,m+2,...,n，并且其中uk,vk∈r。

当且仅当对于所有的ak≠0，k＝1,2,...,m，条件成立时，系统是渐近稳定的。

f的第j个特征值由λj(f)表示，f^h表示f的共轭转置，符合supt∈[-τ,0]表示f(t)在t∈[-τ,0]上的上确界。

从证明结论可以看出，本发明给出了一类奇异时滞系统的简单的稳定性的判别方法，因为给出的判别方法是充分必要的，因此系统的稳定性可以被完全描述。

如图2所示，本发明实施例提供的一类奇异时滞系统的渐近稳定性维持方法，包括以下步骤：

根据本发明任一技术方案提供的一类奇异时滞系统的渐近稳定性判别方法判别该类奇异时滞系统的渐近稳定性；

利用维持该类奇异时滞依赖系统稳定性的条件，以提高该类奇异时滞系统的渐近稳定性。

上述方法应用了本发明提供的一类奇异时滞系统的渐近稳定性判别方法提高了该类奇异时滞系统的渐近稳定性。

最后应当说明的是:以上实施例仅用以说明本发明的技术方案而非对其限制；尽管参照较佳实施例对本发明进行了详细的说明，所属领域的普通技术人员应当理解：依然可以对本发明的具体实施方式进行修改或者对部分技术特征进行等同替换；而不脱离本发明技术方案的精神，其均应涵盖在本发明请求保护的技术方案范围当中。