基于特征值理论的多级轴流压气机失速边界的预测方法与流程

本发明涉及一种多级轴流压气机失速边界的预测方法，尤其涉及一种基于特征值理论的多级轴流压气机失速边界的预测方法，属于叶轮机
技术领域：
。
背景技术：
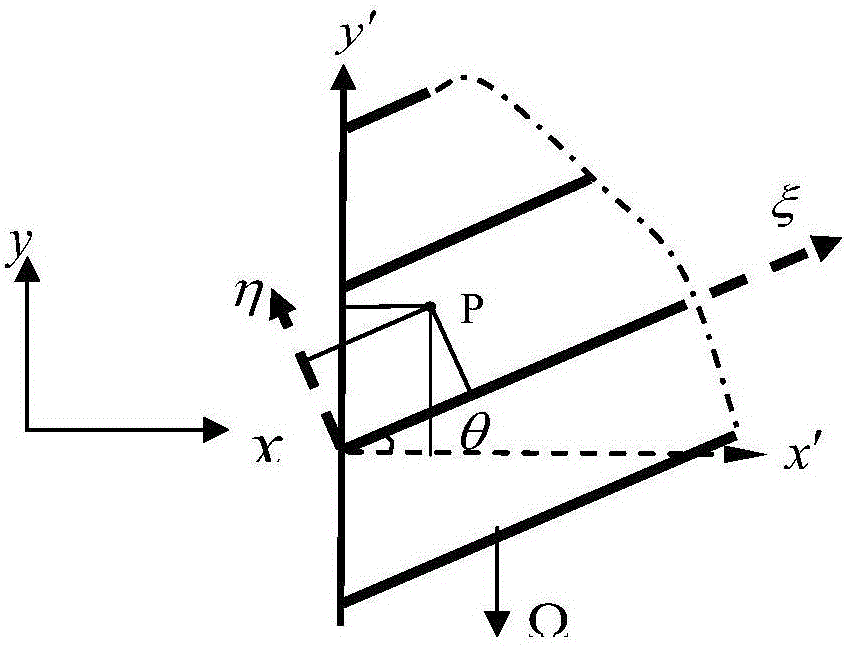
：现有技术中，常见的旋转失速稳定性模型通常是不考虑径向扰动的二维模型。而现在可用的三维稳定性模型非常有限，大多数是三维不可压稳定性模型，并不能满足高速压气机/风扇的需要。为了建立三维稳定性模型，一些研究者也进行了很多尝试。需要强调的是：除了模型本身难度外，其数值求解方法也阻碍了三维稳定性模型的发展，例如，Ludiwig虽然已经建立了的三维不可压稳定性模型，但是由于没有合适的数值求解方法，最终也不了了之了。因为稳定性特征方程是一个复数特征矩阵行列式，没有解析表达式，对自变量的导数也无法表达，而使用Newton-Raphson法、法等传统迭代方法求解时，解的收敛方向不受控制，由于特征方程经常会有多解的情况，并且有些解还超出了物理意义的范围，即使对迭代的初始值做出调整，也很难控制计算结果的收敛方向。技术实现要素：综上所述，确有必要提供一种可以考虑任意阶径向扰动的三维可压缩旋转失速稳定性模型，该模型可以用于多级轴流压气机旋转失速稳定性的研究，且在理论上，可以处理存在机匣处理情况的压气机稳定性问题。一种多级轴流压气机失速边界的预测方法，包括：根据轴流压气机旋转失速先兆的情况，采用小扰动理论，建立刻画流场的三维可压缩Euler方程；运用谐波分解和色散关系，并在每一个流域的轮毂和叶尖处都建立边界条件，其中，每一个流域的解为由可沿上游和下游传播的压力扰动波和随主流速度传播的涡波、熵波组成；将转子和静子采用三维半激盘模型进行模化，并在界面处采用模态匹配技术、守恒定律以及压气机损失特性的表征条件，得到求解线化流场的特征值问题；通过求解该特征值问题得到压缩系统的特征扰动频率，并且通过特征扰动频率判断系统稳定性，系统稳定性的判断标准：在稳定性模型中假定所有扰动量都含有随时间的变化项eiωt，其中扰动频率ω为复数，表示为ω＝ωR+iωI；因此当频率的虚部ωI>0时，扰动随时间发展是衰减的，系统稳定；反之ωI<0，扰动随时间放大，系统失稳。多级轴流压气机划分为叶片区和非叶片区，并设流动为无粘绝热可压缩流动，主流为均匀流，且着眼于压气机失速先兆的情况，即线性小扰动假设；在非叶片区中，主流速度是二维的，忽略径向主流速度；扰动速度为三维扰动；在叶片区中，将有弯度和扭转的叶片用平板叶栅代替，内部的主流速度为一维的，同样的忽略径向主流速度，考虑径向扰动速度的影响。非叶片区的控制方程主要是由质量连续方程、动量方程和能量方程组成。在硬壁面给出的边界条件为无穿透、无滑移以及零振动条件，通过应用三角函数级数的形式，表示径向特征函数。沿轴向向上游或向下游传播的轴向波数表达式为：αmn±j=Mx(βmMy+ωa0)±(βmMy+ωa0)2+(1-Mx2)[βm2+(kmn+j)2](1-Mx2),]]>其中，βm表示周向波数：βm=mrm;]]>rm是叶栅通道中的平均半径，Mx、My指的是马赫数在轴向和周向的分量，a0表示声音的传播速度。叶片区域采用一维的半激盘模型，叶片通道中包含一维的弦向流动，绝对坐标系为(x,y,z)，随动坐标系(x′,y′,z′)，而随动的叶栅弦向坐标系为(ξ,η,z)，不考虑在垂直叶栅弦向的扰动量变化，因此叶栅弦向坐标系为(ξ,z)，叶片区的控制方程包括质量连续方程，弦向动量方程，径向动量方程和能量方程组成。求解得到一个封闭的方程组：Qmn(ω)(9K×9K)·X‾mn(9K)=0,]]>其中，K是叶排数；对于两级压气机，det[Qmn(ω)]＝0，通过求解上式，得到系统的扰动频率，通过分析扰动频率的虚部来判断系统的稳定性。相对于现有技术，本发明提供的多级轴流压气机失速边界的预测方法，以特征值理论为基础，提供了一种可以考虑任意阶径向扰动的三维可压缩旋转失速稳定性模型，可以用于多级轴流压气机旋转失速稳定性的预测，且可以处理存在机匣处理情况的压气机稳定性问题。附图说明图1为本发明实施例提供的半激盘法叶栅通道示意图。图2为本发明实施例提供的转子叶栅坐标系统转换的示意图。图3为本发明实施例提供的多级压气机叶栅示意图。图4为本发明实施例提供的两级压气机模态系数分布示意图。图5为NASA两级风扇的通道的示意图。图6为为NASA两级风扇的整体性能。图7为NASA两级风扇100％转速时的气动参数，其中(a)进口轴向速度；(b)进口静压；(c)损失系数(d)损失系数的导数。图8为NASA两级风扇100％转速时的稳定性预测结果。图9为延迟时间对NASA两级风扇100％转速时稳定性的影响。具体实施方式下面将结合附图详细说明本发明实施例的基于特征值理论的多级轴流压气机失速边界的预测方法。本发明实施例提供的基于特征值理论的多级轴流压气机失速边界的预测方法，包括如下步骤：首先，根据轴流压气机旋转失速先兆的情况，采用小扰动理论，建立刻画流场的三维可压缩Euler方程；其次，运用谐波分解和色散关系，并在每一个流域的轮毂和叶尖处都建立边界条件，其中，每一个流域的解都是由可以沿上游和下游传播的压力扰动波和仅随主流速度传播的涡波、熵波组成的；再次，将转子和静子采用三维半激盘模型进行模化，并在界面处采用模态匹配技术、守恒定律以及压气机损失特性的表征条件，得到求解线化流场的特征值问题；最后，通过求解该特征值问题得到压缩系统的特征扰动频率，并且通过特征扰动频率判断系统稳定性，系统稳定性的判断标准：在稳定性模型中假定所有扰动量都含有随时间的变化项eiωt，其中扰动频率ω为复数，表示为ω＝ωR+iωI；因此当频率的虚部ωI>0时，扰动随时间发展是衰减的，系统稳定；反之ωI<0，扰动随时间放大，系统失稳。请一并参阅图1至图3，在模型中，多级轴流压气机将划分为叶片区和非叶片区，它们各自有不同的控制方程，并假设流动为无粘绝热可压缩流动，主流为均匀流，且着眼于压气机失速先兆的情况，即线性小扰动假设。另外，在非叶片区中，主流速度是二维的，忽略了占比重比较小的径向主流速度，但是扰动速度为三维扰动；在叶片区中，将有弯度和扭转的叶片用平板叶栅代替，内部的主流速度看成是一维的，同样的忽略径向主流速度，考虑径向扰动速度的影响。建立非叶片区控制方程：非叶片区的控制方程主要是由质量连续方程、动量方程和能量方程组成。∂ρ∂t+▿·(ρV→)=0---(1)]]>DV→Dt+1ρ0▿p=0---(2)]]>1P0DpDt-kρ0DρDt=0---(3)]]>式中：“0”代表平均量，k为空气的比热比，ρ为密度，代表速度，p为压力。可以通过使用分离变量法和级数展开的形式求解以上偏微分方程，最终得到偏微分方程的解如下：pj(x,y,z,t)=Σm=-∞+∞Σn=1+∞[p‾mn+jeiαmn+j(x-xj)ψmn+j(z)+p‾mn-jeiαmn-j(x-xj)ψmn-j(z)]ei(βmy+ωt)---(4)]]>ρj=Σm=-∞+∞Σn=1+∞1(a0j)2(ψmn+j(z)eiαmn+j(x-xj)p‾mn+j+ψmn-j(z)eiαmn-j(x-xj)p‾mn-j)+ρ‾vmn+jψvmn+j(z)e-iω+βmVU(x-xj)ei(βmy+ωt)---(5)]]>uj=Σm=-∞+∞Σn=1+∞-1ρ0j(αmn+jψmn+j(z)eiαmn+j(x-xj)p‾mn+j(ω+αmn+jUj+βmVj)+αmn-jψmn-j(z)eiαmn-j(x-xj)p‾mn-j(ω+αmn-jUj+βmVj))+(βmUv‾vmn+jω+βmV-ikvmn+jUw‾vmn+jω+βmV)ψvmn+j(z)e-iω+βmVU(x-xj)ei(βmy+ωt)---(6)]]>vj=Σm=-∞+∞Σn=1+∞-1ρ0j(βmψmn+j(z)eiαmn+j(x-xj)p‾mn+j(ω+αmn+jUj+βmVj)+βmψmn-j(z)eiαmn-j(x-xj)p‾mn-j(ω+αmn-jUj+βmVj))+v‾vmn+jψvmn+j(z)e-iω+βmVU(x-xj)ei(βmy+ωt)---(7)]]>wj=Σm=-∞+∞Σn=1+∞1ρ0j(kmn+jφmn+j(z)eiαmn+j(x-xj)p‾mn+ji(ω+αmn+jUj+βmVj)+kmn-jφmn-j(z)eiαmn-j(x-xj)p‾mn-ji(ω+αmn-jUj+βmVj))+w‾vmn+jφvmn+j(z)e-iω+βmVU(x-xj)ei(βmy+ωt)---(8)]]>其中，“m”是周向模态，“n”是径向模态；“ω”是待求的压缩系统的扰动频率，它是一个复数频率，其实部ωr表示扰动的实际频率，虚部ωi表示扰动的阻尼，也是本模型判断压缩系统稳定性的关键参数。p、ρ、u、v、w和U、V、αmn、βm分别表示压力、密度、轴向速度、周向速度、径向速度的小扰动量和轴向主流速度、周向主流速度、轴向波数，周向波数。在推导非叶片区控制方程的解的过程中，需要结合边界条件。首先，在硬壁面给出的边界条件为无穿透、无滑移以及零振动条件，通过应用三角函数级数的形式，可以表示径向特征函数，如下ψ和φ：ψmn±j(z)=ψvmn±j(z)=cos(kvmn±jz)---(9)]]>φmn±j(z)=φvmn±j(z)=sin(kvmn±jz)---(10)]]>径向波数为：kmn=nπh,(n=0,1,2,...N)---(11).]]>在压气机的周向应满足周期性条件，可采用周向波数的形式。其中βm表示周向波数，表达式为：βm=mrm---(12)]]>rm是叶栅通道中的平均半径。另外，“j”表示第j个无叶片区域，“+”代表扰动向下游传播，“-”代表扰动向上游传播。表示沿轴向向上游或向下游传播的轴向波数，其表达式为：αmn±j=Mx(βmMy+ωa0)±(βmMy+ωa0)2+(1-Mx2)[βm2+(kmn+j)2](1-Mx2)---(13)]]>其中，Mx、My指的是马赫数在轴向和周向的分量，a0表示声音的传播速度。请一并参阅图4，至此，要确定一个无叶片区域内单一模态波(m,n)对应的扰动量的大小，需得到以下5个模态系数：p‾mn+j,p‾mn-j,v‾vmn+j,w‾vmn+j,ρ‾vmn+j---(14)]]>其中，是压力波的模态系数，是涡波的模态系数，是熵波的模态系数。建立叶片区控制方程：叶片区域可使用一维的半激盘模型，叶片通道中只有一维的弦向流动。绝对坐标系为(x,y,z)，随动坐标系(x′,y′,z′)，而随动的叶栅弦向坐标系为(ξ,η,z)，由于模型不考虑在垂直叶栅弦向的扰动量变化，因此又可以说叶栅弦向坐标系为(ξ,z)。下面给出线化欧拉方程是建立在相对坐标系(ξ,z)下的，若Ω＝0则为静子，否则为转子。与非叶片区控制方程的组成一样，叶片区的控制方程是由质量连续方程，弦向动量方程，径向动量方程和能量方程组成的。可以Wc表示弦向平均速度，q表示弦向扰动速度，w表示径向扰动速度，建立的叶片区的控制方程如下：∂ρ∂t+Wc∂ρ∂ξ+ρ0(∂q∂ξ+∂w∂z)=0---(15)]]>∂q∂t+Wc∂q∂ξ=-1ρ0∂p∂ξ---(16)]]>∂w∂t+Wc∂w∂ξ=-1ρ0∂p∂z---(17)]]>1P0(∂p∂t+Wc∂p∂ξ)+k(∂q∂ξ+∂w∂z)=0---(18).]]>与求解非叶片区控制方程的方法一样，最终可以得到叶片区压力、密度、弦向速度和径向速度扰动量的解为：pck(x,y′,z,t)=Σm=-∞+∞Σn=1+∞[eiαcmn+k(x-xk)ψcmn+k(z)p‾cmn+k+eiαcmn-k(x-xk)ψcmn-k(z)p‾cmn-k]ei(ω-mΩ)t+iβmy′---(19)]]>ρck(x,y′,z,t)=Σm=-∞+∞Σn=1+∞1(a0k)2(ψcmn+k(z)eiαcmn+k(x-xk)p‾cmn+k+ψcmn-k(z)eiαcmn-k(x-xk)p‾cmn-k)+ρ‾cvmn+kφcvmn+k(z)e-i(ω-mΩ)+βmWcksinθkWckcosθk(x-xk)ei(ω-mΩ)t+iβmy′---(20)]]>qck(x,y′,z,t)=Σm=-∞+∞Σn=1+∞-1ρ0k(αcmn+kcosθ+βmsinθ)eiαcmn+k(x-xk)ψcmn+k(z)p‾cmn+k[(ω-mΩ)+Wc(αcmn+kcosθ+βmsinθ)]+(αcmn-kcosθ+βmsinθ)eiαcmn-k(x-xk)ψcmn-k(z)p‾cmn-k[(ω-mΩ)+Wc(αcmn-kcosθ+βmsinθ)]-ikcvmn+kWck(ω-mΩ)e-i(ω-mΩ)+βmWcksinθkWckcosθk(x-xk)ψcvmn+k(z)w‾cvmn+kei(ω-mΩ)t+iβmy′---(21)]]>wck(x,y′,z,t)=Σm=-∞+∞Σn=1+∞1ρ0kcmn+ke-iαcmn+k(x-xk)φcmn+k(z)p‾cmn+ki[(ω-mΩ)+Wc(αcmn+kcosθ+βmsinθ)]+kcmn+ke-iαcmn-k(x-xk)φcmn-k(z)p‾cmn-ki[(ω-mΩ)+Wc(αcmn-kcosθ+βmsinθ)]+w‾cvmn+kφcvmn+k(z)e-i(ω-mΩ)+βmWcksinθkWckcosθk(x-xk)ei(ω-mΩ)t+iβmy′---(22)]]>其中，式中是k排叶栅内的声速，Mc是相对坐标系下弦向的马赫数，Ω表示转子的转频，Wc表示叶栅弦向的主流速度，轴向波数αcmn的表达式为：αcmn±kcosθ+βmsinθ=Mca0ck(ω-mΩ)±(ω-mΩ)2(a0ck)2-(1-Mc2)(kcmn±k)2(1-Mc2)---(23)]]>其中，kcmn是径向特征函数ψcmn(z)的特征值。径向特征函数之间的关系式如下：ψcmn±k=ψcvmn+k=cos(kcmn+kz)---(24)]]>φcmn±k=φcvmn+k=sin(kcvmn+kz)---(25)]]>径向波数为：kcmn=nπh,(n=0,1,2,...N)---(26).]]>对于转子和静子来说，唯一的区别在于Ω。同样，如果要确定叶片域内扰动量的大小，也必须要得到每个扰动波的所有模态系数，对于一个叶栅来说，确定一个模态的系数共有四个，即：界面匹配在获得基本方程的解析解之后，在界面上采用模态匹配技术、守恒定律以及可以表征压气机损失特性的条件，将界面上的小扰动解析解建立联系。由于总的压力损失和流量转向特性对预测结果非常重要，在这个模型中，假定的流动转向和损失发生在叶片前缘。因此，最终给出的前缘匹配条件如下：ρjUj+ρ0juj=(ρkUk+ρ0kqk)cosθk---(27)]]>Tt′j=pjRρ0-(a0j)2kRρ0ρj+1cp(Ujuj+Vrjvj)=pkRρ0-(a0k)2kRρ0ρk+Wckqkcp=Tt′k---(28)]]>wk＝wj+1(29)ptj-ptk=11+iωτloss12ξskρj(Wj)2+ξskρ0j[Ujuj+Vrjvj]+12Uj∂ξsk∂tanβkρ0j(Wj)2(vj-ujtanβk)---(30)]]>其中，Tt′表示总温扰动，R为空气常数，为相对周向速度，τloss是延迟时间,是相对总压损失系数：ξsk=Ptj-Ptj+1ρj(Wj)2/2---(31)]]>非叶片区的总压扰动为：ptj=(S1j-k(Mj)22S2j)pj+(Wj)22S2jρj+ρ0jUjS2juj+ρ0jS2jVrjvj---(32)]]>其中，M表示马赫数，和分别为：S1j=[1+κ-12(Mj)2]κκ-1S2j=[1+κ-12(Mj)2]1κ-1---(33)]]>叶片区的总压扰动为：ptk=(S1k-k(Mck)22S2k)pk+(Wck)22S2kρk+ρ0kS2kWckqk---(34)]]>其中，S1k=[1+κ-12(Mck)2]κκ-1S2k=[1+κ-12(Mck)2]1κ-1---(35)]]>在稳定性模型中，假定在叶片后缘没有流动的偏转和损失发生，所以5个尾缘匹配条件如下：pk＝pj+1(36)ρk＝ρj+1(37)wk＝wj+1(38)qkcosθ＝uj+1(39)qksinθ＝vj+1(40)假定来流无畸变无扰动，出口无反射：p‾mn+1=ρ‾vmn+1=v‾vmn+1=w‾vmn+1=0,(n=1,2,3...N)---(41)]]>p‾mn-(J+1)=0,(n=1,2,3...N)---(42)]]>最终得到一个封闭的方程组：Qmn(ω)(9K×9K)·X‾mn(9K)=0---(43)]]>其中，K是叶排数。对于两级压气机，Qmn(ω)和分别是：Qmn(ω)=C1,1C1,2...C1,5.........C4,1C4,2...C4,5C5,2...C5,5C5,6...C5,10............C9,2...C9,5C9,6...C9,10...............C32,29...C32,32C32,33...C32,36............C36,29...C36,32C36,33...C36,36mn---(44)]]>X‾mn=p‾mn-1p‾cmn+1...v‾vmn+5w‾vmn+5T---(45)]]>由于一定存在，且不为零，因此：det[Qmn(ω)]＝0(46)因此，最终得到一个关于求解线化流场的特征值问题。通过求解上式，可以得到系统的扰动频率，通过分析扰动频率的虚部来判断系统的稳定性。在模型推导过程中已经将两级压气机稳定性的物理问题转化为求解线化流场的特征值问题。det[Qmn(ω)]36×36＝0由于这个方程常常不是普通的实变代数方程或一般的简单复数型超越方程，而是一个复数矩阵行列式，因此，可采用奇异值分解的方法求解。奇异值分解方法不但可以精确诊断特征矩阵的奇异性来源，还可以处理病态矩阵问题以及大部分的最小二乘问题，因此，针对两级压气机稳定性的特征矩阵，选择采用奇异值分解获得矩阵条件数的方法来判定矩阵奇异性。奇异值分解法所基于的线性代数理论：设X是M×N阶复矩阵，因此X可以分解为一个M×M阶酉矩阵U，一个M×N阶对角矩阵S和一个N×N阶酉矩阵V的转置矩阵的乘积，即(X)＝(U)*S*(VT)其中，S＝diag(σ1，σ2，……，σi)，σi≥0(i＝1，…，r)，r＝rank(A)；U和V分别是X的奇异向量，S是X的奇异值。如果σi中一个或多个为零或者非常小，则可以判定矩阵奇异。因此奇异值分解方法可以清晰地判断矩阵的奇异性。形式上，矩阵的条件数可以定义为最大与最小奇异值之比。理论上，条件数无穷大时，该矩阵奇异。条件数越大，矩阵病态越严重。求解本模型特征值方程即是寻找正确的σi值，使得矩阵X奇异。作为具体的实施例，对NASA两级风扇稳定性算例验证。为了评估本模型对多级压气机稳定性失速先兆点预测能力，将本模型应用于第一级转子是小展弦比的NASA两级风扇(如图5)100％转速时失速起始点的研究。其中，NASA两级风扇失速实验通过在不同的站位同时采集径向11不同点的数据来研究设计转速从50％至100％的失速边界。在设计情况中，质量流量是33.248kg/s，总压力比为2.399和绝热效率为0.849。表1显示了一些设计参数和图6示出了整体性能。NASA两级风扇的几何结构和性能参数的细节在NASA报告中，详细的实验数据由Urasek等人提供。表1NASA两级风扇设计参数模型计算时需要输入一些多级轴流压气机的几何数据和流场数据，其中包括压气机的半径、叶片的弦长以及压力、速度、相对总压损失系数和其对相对进口角的导数等参数。NASA实验给出了通道的每一个站位上的11处不同径向位置的流场数据，由于模型有均匀流假设，因此首先要对需要的每一个通道截面的流场求出其平均值，用平均流场数据来表征通道截面的流场。在NASA的实验结果中可以看出径向速度相对轴向速度和周向速度较小，可以忽略，这与模型的假设相一致，且会使计算结果更为准确。模型输入数据的相对进口角和相对出口角使用流场中的速度关系求出；另外，实验给出的数据都是两级压气机处于稳态状态下的数据，为了能够更好地说明问题，需要对实验数据进行外推以验证模型的合理性。本研究使用的外推方式是，损失系数和流速之间的变化关系可以通过已知7个实验数据拟合出来，然后降低流速的损失系数可以从该关系中求解出来。图7示出了NASA两级风扇的气动数据随质量流量的变化关系，如进口轴向速度，进口静压，损失及其导数随流量的变化关系。可以看出，随着质量流量的减小，进口轴向速度也降低，压力缓慢上升，损失系数变大。图8示出了NASA的两级风扇的在100％的设计工作速度的预测结果。其中，x-轴表示质量流量，y轴表示衰减因子DF，其定义为rmωI/(mU0)或者表示相对速度RS，其定义为60ωr/(2πmΩ)。值得注意的是，随着节流的进行，质量流量减小，衰减因子也在减小。当流量是33.9kg/s时，衰减因子穿过稳定的临界值，并且该模型的数值结果的相对转速为52.5％的设计工作速度。失速开始点的相对误差为0.9％，与实验的结果相比，这是比较准确的合理预测。另外，还研究了延迟时间对稳定性的影响。通常情况下，应该从实验测量来获得时间延迟的精确的值。而在本实施例中，可以定义延迟时间为：τloss＝c/Wc其中，c是叶片的弦长，Wc是气流在叶栅弦向的平均流。进一步研究延迟时间对两级压气机稳定性的影响，图中显示了NASA两级压气机100％设计工作转速下，扰动波的衰减系数和相对周向速度在不同延迟时间的计算结果。图9表示在没有时间延迟，给定的时间延迟和双时间延迟的不同的情况下，NASA两级风扇在100％的设计工作速度的扰动波衰减因子和相对周速度的计算结果。从计算结果中可以看出，延迟时间对扰动波的衰减系数几乎没有影响，对相对周向速度的影响也不是很大。另外，本领域技术人员还可在本发明精神内做其他变化，当然，这些依据本发明精神所做的变化，都应包含在本发明所要求保护的范围之内。当前第1页1 2 3