基于缺损数据的非线性特征提取和分类方法与流程

本项发明涉及信息处理技术中的数据挖掘方向，可应用于缺损数据的非线性特征挖掘领域，特别涉及一种基于缺损数据的非线性特征提取和分类方法。

背景技术：

科学的进步，特别是信息产业的发展，把我们带入了一个崭新的信息时代。在信息时代的科学研究过程中，不可避免的会遇到大量的数据，如全球气候模型、图像分类系统、文本聚类和基因序列的建模等。人们虽然可以获取大量的信息资源，但由于缺乏挖掘数据背后隐藏的知识的手段，人们无法更好的发现数据中存在的关系和规则，也无法很好的根据现有的海量数据预测未来的发展趋势。目前，数据挖掘引起了信息产业界和整个社会的极大关注。而在数据挖掘的过程中，面对的海量数据对于我们想要研究的具体方向往往是不完整的。缺损数据产生的原因很多，例如：有些数据有时有些属性内容缺失；有些属性在当时被认为是不必要的；有些属性的值根本不能直接观察获得等。举一个常见的例子，在视频监控中，监控目标可能被其它物体部分遮挡，此时只能获取监控目标的部分图像，这些被遮挡的图像即为缺损数据。由于数据的缺损在现实世界中普遍存在，如何挖掘出缺损数据的本质信息和关联，成为数据挖掘领域中备受关注的一个问题。

目前所形成的对缺损数据挖掘的一个通用方法：先将缺损整数据中的缺失值按照某种原则和方法进行填充，再挖掘出填充后数据的本质信息。现有的对缺损数据的缺损值填充的方法主要有人工填补法、单值填补法、类均值填补法、推断填补法、EM算法等等。目前，这些算法被广泛的用于缺损数据挖掘，它们在挖掘缺损数据之间的线性关系方面取得了值得肯定效果，但是它们都无法很好的挖掘缺损数据之间的非线性关系。基于此，迫切需要在缺损数据挖掘中引入非线性降维即流形学习方法。

近几年来，流形学习在机器学习领域成为了一个新的热点问题。现有的传统数据降维方法，如主分量分析(PCA)、多维尺度变换(MDS)等，降维后得到的低维数据能保持高维数据点之间的全局线性关系。但在实际的应用分析中，这些高维数据可能嵌入在一个非线性的流形，数据点之间并不具有全局的线性关系。比如，在动态物体的监控视频中，采自视频序列的图像维数为图像中的像素点的个数，这些图像可以视为高维空间中的高维数据点。当视频序列描述运动物体时，运动物体在每帧图像中的坐标包含了这帧图像的主要信息。因此，这些视频实际上嵌入在一个非线性的低维流形，视频帧之间并不具有全局的线性关系。流形学习方法相对于传统的线性降维方法，能够比较好地挖掘隐藏在高维数据中的流形结构。其中代表性的流形学习方法有等距映射(ISOMAP)、局部线性嵌入(LLE)、拉普拉斯特征映射(LE)和局部切空间对齐(LTSA)。流形学习虽然具有参数少，实现简单，计算快等优点，但其要求数据具有近似完整的流形结构，所以当数据缺损不完整时，流形学习算法的效果会受到很大的影响。

技术实现要素：

本发明的目的在于克服现有技术的不足，提出一种基于缺损数据的非线性特征提取和分类方法，基于流形学习的基本思想，从构造局部邻域、提取局部坐标和局部坐标对齐三个方面提出一种适用于缺损数据的算法，实现缺损数据的非线性特征提取和分类。

本发明解决其技术问题所采用的技术方案是：

一种基于缺损数据的非线性特征提取和分类方法，包括如下步骤：

采用缺损数据的距离估计方法来构造数据点的局部邻域集和局部邻域集对应的缺失标记集；

构造基于所述局部邻域集和其对应的缺失标记集的核范数正则化模型，并使用动态自适应迭代算法求解该模型来提取局部坐标；

对齐所述局部坐标，获得全局坐标。

优选的，所述采用缺损数据的距离估计方法来构造数据点的局部邻域集和局部邻域集对应的缺失标记集，包括：

(1)对于每个数据点x_i(i＝1,2,…,n)，定义一个缺失性标记向量f_i＝(f_i1,f_i2,…,f_im)^T，其中f_it＝0当且仅当数据点x_i中的第t个属性值缺失，否则f_it＝1；用如下公式表示两个具有缺失值的数据点x_i和x_j之间的距离：

$sim(x_i,x_j)=\frac{\left|\underset{t\∈I}{\Σ}{x}_{it}{x}_{jt}\right|}{\sqrt{\underset{t\∈I}{\Σ}{x_{it}}^2}\sqrt{\underset{t\∈I}{\Σ}{x_{jt}}^2}},I=\left\{t\right|f_{it}\×f_{jt}=1\}$

其中，i＝1,2,…,n；j＝1,2,…,n；I表示数据点x_i和x_j已知数值的指标集；

(2)对于每个数据点x_i使用上述公式计算出其对应的k个近邻点；

(3)构造数据点x_i的局部邻域集和其对应的缺失标记集F_i。

优选的，新的核范数正则化模型如下：

其中，⊙表示矩阵之间的点乘，c和Z为模型的解，e＝[1,1,…,1]^T，λ表示正则化参数。

优选的，所述使用动态自适应迭代算法求解该模型具体指获取模型的最优解c_*和Z_*。

优选的，所述获取模型的最优解c_*的方法如下：

(1)令由于是凸函数，则可以通过如下公式获取c_*最优解：

(2)基于上式求得最优解c_*的表达式：

c_*＝(F_i⊙(X_i-Z_*))e·/(F_i)e

其中，·/表示矩阵或向量之间的点除。

优选的，所述获取模型的最优解Z_*的方法如下：

(1)获取最优解Z_*的KKT条件，如下：

其中，表示核函数的次梯度集合；

(2)对上述公式进行等同变换得到：

(3)在其两侧同时加上Z_*进一步变换得到：

(4)根据上式求解如下最小化问题来获取最优解Z_*：

$\underset{Z}{min}\frac{1}{2}\left|\right|Z-Y_{*}|{|}_F^2+\mathrm{\λ}|\left|Z\right|{|}_{*}$

(5)由Z_*＝S_λ(Y_*)给出上式的最优解，其中S_λ(·)表示收敛算子，令Y的奇异值分解为则Σ_λ＝diag[(λ₁-λ)₊,…,(λ_r-λ)₊]并且(λ_i-λ)₊＝max(λ_i-λ,0)，U_Y和V_Y分别表示Σ_λ对应的左右奇异向量组成的矩阵。

优选的，所述动态自适应迭代算法具体指动态调整正则化参数λ，使得最优解Z_*的秩d^*最终位于一个合理的范围内，而非某一个固定值。

优选的，对最优解Z_*进行SVD分解，即Z_*＝U_iΣ_iV_i^T，得到d^*维的局部坐标

优选的，所述对齐所述局部坐标，获得全局坐标，具体包括：

(1)令X_i中对应的数据点的全局低维坐标为并最小化对齐成本函数，如下：

$E^{*}\left(T\right)=\underset{i}{\Σ}\underset{L\∈R^{d\×d^{*}}}{\underset{c\∈R^d}{min}}\left|\right|T_i-{\mathrm{ce}}^T-{\mathrm{L\Θ}}_i^{*}|{|}_F^2;$

(2)求得上式的最优解c_i＝T_ie/k，其中是局部坐标的广义逆；

(3)根据求得其中V_i是由Z_*的最大的d^*个奇异值对应的右奇异向量构成的矩阵；

(4)将所述对齐成本函数转换为如下形式：

$\underset{T}{min}\underset{i}{\Σ}\left|\right|E_i|{|}_F^2=\underset{T}{min}\underset{i}{\Σ}|\left|T_{i}J(I-V_i{V}_i^T)\right|{|}_F^2$

其中，J＝I-ee^T/k；

(5)令W_i＝J(I-V_iV_i^T)，S_i为选择矩阵，满足TS_i＝T_i，上述公式转换成如下形式：

$\underset{T}{min}\underset{i}{\Σ}\left|\right|E_i|{|}_F^2=\underset{T}{min}\underset{i}{\Σ}|\left|{\mathrm{TS}}_i{W}_i\right|{|}_F^2=\underset{T}{\min trace}\left({\mathrm{T\ΦT}}^T\right)$

其中：

$\mathrm{\Φ}=\underset{i}{\Σ}{S}_{i}J(I-V_i{V}_i^T){(I-V_i{V}_i^T)}^T{J}^T{S}_i^T$

(6)求解矩阵Φ的最小的第2个到第d+1个非零特征值对应的特征向量[u₂,…,u_d+1]构成最优全局低维坐标T＝[u₂,…,u_d+1]^T。

本发明具有如下有益效果：

(1)提出一种适用于缺损数据的距离估计方法，从而可以准确地构造每个缺损数据点的局部邻域；

(2)提出一种新的核范数正则化模型以及求解该模型的动态自适应迭代算法，从而快速准确地提取局部坐标；

(3)通过对齐局部坐标，获得全局坐标。

以下结合附图及实施例对本发明作进一步详细说明，但本发明的一种基于缺损数据的非线性特征提取和分类方法不局限于实施例。

附图说明

图1为本发明方法的流程图示意图；

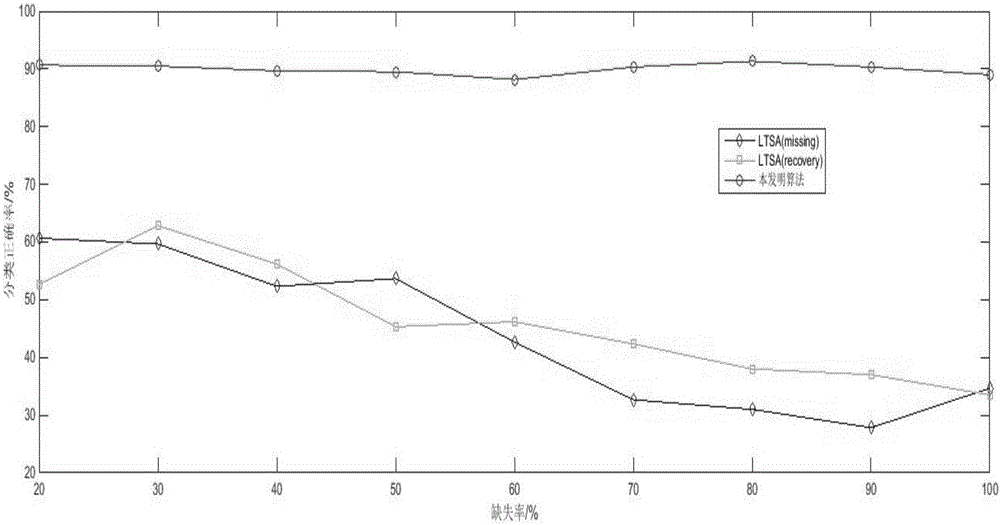
图2为本发明方法与其他方法在不同缺失率图像集上其分类正确率的变化图。

具体实施方式

参见图1，本发明提供的一种基于缺损数据的非线性特征提取和分类方法，包括如下步骤：

步骤101：采用缺损数据的距离估计方法来构造数据点的局部邻域集和局部邻域集对应的缺失标记集。

对于每个数据点x_i(i＝1,2,…,n)，定义一个缺失性标记向量f_i＝(f_i1,f_i2,…,f_im)^T，其中f_it＝0当且仅当数据点x_i中的第t个属性值缺失，否则f_it＝1，则整个数据集X＝(x₁,x₂,…,n)的缺失性标记矩阵为F＝(f₁,f₂,…,f_n)。本发明基于余弦相似度的基本思想，将数据点看成其对应的向量，则两个具有缺失值的数据点x_i和x_j之间的距离可以表示为

$sim(x_i,x_j)=\frac{\left|\underset{t\∈A}{\Σ}{x}_{it}{x}_{jt}\right|}{\sqrt{\underset{t\∈A}{\Σ}{x_{it}}^2}\sqrt{\underset{t\∈A}{\Σ}{x_{jt}}^2}},A=\left\{t\right|f_{it}\×f_{jt}=1\}---\left(1\right)$

其中A表示数据点x_i和x_j已知数值的指标集。向量的余弦相似度的范围为[0,1]，相似度越大，距离越小。对于每个数据点x_i使用公式(1)可以得到其对应的k个近邻点，从而构造数据点x_i的局部邻域集和其对应的缺失标记集F_i。

步骤102：构造基于所述局部邻域集和其对应的缺失标记集的核范数正则化模型，并使用动态自适应迭代算法求解该模型来提取局部坐标。

本发明面向缺损数据所提出的一种新的核范数正则化模型如下：

进一步的，提出一种动态自适应迭代算法对于公式(2)进行求解。

令由于是凸函数，则其最优解c_*和Z_*的KKT-条件分别如下：

●

●

其中，表示核函数的次梯度集合。

基于KKT-条件(3)可以得到最优解c_*的表达式：

其中，·/表示矩阵或向量之间的点除。

同理，基于KKT-条件(4)可以得到最优解Z_*等同于满足公式在其两侧同时加上Z_*可得可以明显得出(由公式推导得出)，求解最优解Z_*等价于求解如下最小化问题：

$\underset{Z}{min}\frac{1}{2}\left|\right|Z-Y_{*}|{|}_F^2+\mathrm{\λ}|\left|Z\right|{|}_{*}---\left(6\right)$

其中Y_*由Z_*决定。公式(6)的最优解可由Z_*＝S_λ(Y_*)给出，则可以得到：其中S_λ(·)是收敛算子。已知是Y的SVD分解，则可得其中Σ_λ＝diag[(λ₁-λ)₊,…,(λ_r-λ)₊]并且(λ_i-λ)₊＝max(λ_i-λ,0)。

具体的，最优解Z_*可由下面的定点迭代算法进行计算。初始化一个Z，每一次定点迭代方法由两步构成：

●推演：Z→Y＝Z+F_i⊙(X_i-c_*e^T-Z)

●收敛：Y→Z＝S_λ(Y)

综所上述，初始化一个Z^old，本发明提出的动态自适应迭代算法由以下三步构成：

●Z^old→c^new＝(F_i⊙(X_i-Z))e./(F_i)e

●c^new,Z^old→Y＝Z^old+F_i⊙(X_i-c^newe^T-Z^old)

●Y→Z^new＝S_λ(Y)

通过上述分析，可以得出最优解Z_*的秩取决于正则化参数λ。对于一个d维的流形，传统流形学习算法通过构造d维的局部线性近似坐标来获得全局的d维的嵌入坐标。但是，在实际应用中，每个局部邻域的真实维度是很难确定的，尤其是该流形具有噪声或者数据缺损。因此，对于每个局部邻域，其最优解Z_*的秩d^*应该位于一个合理的区间范围内，而不是固定为一个定值，如d。在本发明的交替算法中，将动态调整正则化参数λ，使得最优解Z_*的秩d^*最终位于一个合理的范围[d_min,d_max]内。首先，创造一系列递减的正则化参数λ的值：λ₁,λ₁-τ,λ₁-2τ,…，其中，λ₁和τ是由用户设置的参数值，但由于其对实验效果的影响远远低于d_min和d_max，通常将λ₁设置为F_i(X_i-ce^T)进行SVD分解后的第5个最大的奇异值，τ＝λ₁/10。随着正则化参数λ的值减小，d^*将逐渐增大。如果满足条件d^*<d_min，则继续减少正则化参数λ的值。如果满足条件d^*>d_max，则适当增加正则化参数的值，例如：λ＝λ+τ/2。重复上述过程，直到d^*∈[d_min,d_max]。

总结上述分析过程，本实施例中，可得具体的动态自适应迭代算法流程如下：

输入：数据点x_i的局部邻域集X_i和其对应的缺失标记集F_i，局部邻域秩的合理估计范围[d_min,d_max]。

输出：目标填充矩阵Z^*和c^*，具体步骤如下：

步骤1初始化Z^old＝0，λ是F_i(X_i-ce^T)进行SVD分解后的第5个最大的奇异值，τ＝λ/10,ε＝10-⁵。

步骤2求解公式(2)得到c和Z,具体步骤如下：

步骤2.1求解c^new＝F_i⊙(X_i-Z^old)·/|F_i|。

步骤2.2求解Z^new←S_λ(F_i⊙(X_i-c^newe^T)+F_i^⊥⊙Z^old)，其中F^⊥为缺失标记矩阵F的补集，满足公式F^⊥⊙X+F⊙X＝X。

步骤2.3如果符合条件令d^*为Z^new的秩，进行步骤3。

步骤2.4令Z^old←Z^new，进行步骤2.1。

步骤3动态调整正则化参数λ。

步骤3.1如果符合条件d^*∈[d_min,d_max]，进行步骤4。

步骤3.2如果符合条件d^*<d_min，适当减少正则化参数值λ，例如λ＝λ-τ；进行步骤3.4。

步骤3.3如果符合条件d^*>d_max，适当增加正则化参数值，例如λ＝λ+τ/2；进行步骤3.4。

步骤3.4令Z^old←Z^new，进行步骤2。

步骤4令最优解Z^*＝Z^new和c^*＝c^new。

基于已获得的局部邻域X_i，本发明利用迭代算法求解模型(2)可以获得最优解Z_i＝Z^*和c_i＝c^*。对Z_i进行SVD分解，即：Z_i＝U_iΣ_iV_i^T，可以得到d^*维(其中，d^*∈[d_min,d_max])的局部坐标

步骤103：对齐所述局部坐标，获得全局坐标。

通过对齐步骤102得到的局部坐标Θ^*，获得全局坐标T。令X_i中对应的数据点的全局低维坐标为最小化下列对齐成本函数：

$E^{*}\left(T\right)=\underset{i}{\&Sigma;}\underset{L\&Element;R^{d\&times;d^{*}}}{\underset{c\&Element;R^d}{min}}\left|\right|T_i-{\mathrm{ce}}^T-{\mathrm{L\&Theta;}}_i^{*}|{|}_F^2---\left(7\right)$

对上述成本函数最小化的求解，可以通过如下矩阵获得：

$\mathrm{\&Phi;}=\underset{i}{\&Sigma;}{S}_{i}J\left(I-{\mathrm{\&Theta;}}_i^{*+}{\mathrm{\&Theta;}}_i^{*}\right){\left(I-{\mathrm{\&Theta;}}_i^{*+}{\mathrm{\&Theta;}}_i^{*}\right)}^T{J}^T{S}_i^T---\left(8\right)$

其中，I为合适维度的单位矩阵，J＝I-ee^T/k，S_i为选择矩阵，满足TS_i＝T_i，是局部坐标的广义逆。求解矩阵Φ的最小的第2个到第d+1个非零特征值对应的特征向量[u₂,…,u_d+1]构成最优全局低维坐标T＝[u₂,…,u_d+1]^T。

如图2所示为本发明方法与其他方法在不同缺失率图像集上其分类正确率的变化图。在两个真实图像数据集COIL-20-PROC和CMU PIE上的实验效果验证了本发明的有效性。对比算法有两个，一个是LTSA(missing)，表示将具有缺损数据的图像集直接用LTSA算法降维到低维特征空间；另一个是LTSA(recovery)，表示先用某种填充算法(这里采用的是单值填充算法)对缺损数据集中的缺失值进行填充，然后将填充后得到的图像集用LTSA算法降维到低维特征空间。对上述算法得到的低维嵌入后的结果采用K-NN(K-Nearest Neighbor)分类器进行分类，得到不同对比算法的分类效果。通过表1可以看出本发明在不同缺失程度(缺失像素个数/总像素个数)的COIL-20-PROC图像集上，其分类的准确率都远高于其它对比算法，体现了非常好的效果。通过图2可以看出本发明在不同缺失率(缺失图片个数/总图片个数)的CMU-PIE图像集上，其分类的准确率保持在一个较高且稳定的区间内，具有非常好地鲁棒性。

表1在不同缺失程度COIL-20-PROC图像集上其分类的正确率(％)

以上所述仅为本发明的较佳实施例，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。