一种改进的三角函数切换算法的制作方法

本发明涉及一种三角函数，尤其涉及一种改进的三角函数切换算法。

背景技术：

现有技术中，三角函数分段切换法基本思想是把链式系统的多个输入在时间轴上进行分时处理——即在每一时间段上仅允许一个输入有效而其他输入全部为零，使链式系统在多个输入同时作用下的复合运动分解为单个控制输入下的简单运动，同时以三角函数作为控制输入，结合时间尺度变换技术可使速度输入曲线变得平缓，克服了bang-bang和分段常数法中输入切换处路径不光滑和过高波动的问题。

技术实现要素：

本发明的目的就在于为了解决上述问题而提供一种改进的三角函数切换算法。

本发明通过以下技术方案来实现上述目的：

本发明由链式系统数学模型的三角结构形式知，在控制输入[0,a_isinωt][a_i+1sinωt,0]的二次切换作用下，链式变量的运动在时间τ∈[(k+(i+1)/s)δ,(k+(i-1)/s)δ]上被分解为两部分，即[0,Δz₂,0,…,0]，[Δz₁,0,Δz₃,…,Δz_n]，其中要使包含链式变量{z₃,z₄,…,z_n}的n-2个线性无关的方程有解，v₁必然最少经过n-2次切换输入，由式(3)知v₂最少需要n-1次切换输入，因此三角函数控制输入的切换次数最少为2n-3次，故链式系统路径规划的运动时间被等分的次数不低于2n-3，下面给出具体的证明：

定理1在控制输入

的作用下，两输入n维链式系统可以从初始位形z⁰运动到邻域内的目标位形z^f，其中系统的运动控制时间T最少等分2n-3次；

与式(3)类似，式(4)仍然是将链式系统运动的时间等分为s段，但在每一段上用一个周期的余弦曲线作为控制输入，这样做的好处是同时保证了位移曲线和速度曲线都是光滑的；下面给出算法定理1的数学证明；

证明：时间T被等分为2n-3次，每一个时间段长度为η＝T/(2n-3)，在奇数时间段上t∈[t_2i,t_2i+1]上(i∈{0,1,2,…,n-2})，等分的时间间隔表示为η＝t_2i+1-t_2i,，因此在奇数时间段上的式(4)可以表示为

式(5)中b_2i+1是待定系数，角频率ω＝2π/η，代入到式(21)逐步积分，

类似的，在偶数时间段上t∈[t_2j+1,t_2j+2](j∈{0,1,2,…,n-3})，等分的时间间隔表示为η＝t_2j+2-t_2j+1，因此算法式(4)在偶数段上有，

将式(7)代入到链式系统在时间t∈[t_2i+1,t_2i+2]上积分，得：

通过迭代计算式(6)和式(8)，得到系统运动到时间T的目标位形z^f，

式(9)中含有n个方程和2n-3个待定系数，将所有待定系数重新表示为两个系数矢量B_O＝[b₁,b₃,…,b_2n-3]^T和B_E＝[b₂,b₄,…,b_2n-4]^T，其中B_O和B_E分别称为奇数时间段系数矢量和偶数时间段系数矢量；由式(9)知B_E中n-2个元素满足，

任意给定一组满足式(10)的B_E，当时，B_O中n-1个系数可以由式(9)中剩余的n-1个方程唯一确定；

证毕；

当时，有由式(9)知奇数时间段的系数矢量B_O无解；解决的办法是设置一个中间位形且满足系统的路径规划问题分为两个步骤，第一步先控制系统从初始位形z⁰运动到中间位形z^c，然后将中间位形z^c看成一个新的初始位形，控制系统运动到目标位形z^f；故当时，系统的路径就是以z^c为中间位形、首尾连接的两段路径组成。

本发明的有益效果在于：

本发明是一种改进的三角函数切换算法，与现有技术相比，本发明在多个输入同时作用下的复合运动分解为单个控制输入下的简单运动，同时以三角函数作为控制输入，结合时间尺度变换技术可使速度输入曲线变得平缓，克服了bang-bang和分段常数法中输入切换处路径不光滑和过高波动的问题。

附图说明

图1是三角函数分段切换控制输入下的四状态单链系统路径规划曲线图；

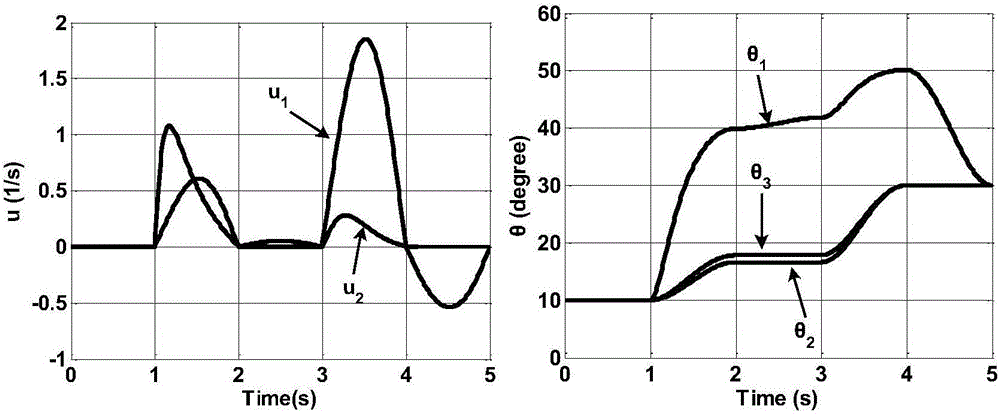
图2所示为三关节非完整机械臂的位移曲线和两部电机的实际控制输入曲线图；

具体实施方式

下面对本发明作进一步说明：

已有算法分析：令分段常数输入那么在时间τ∈[kδ,(k+1)δ]上分段常数控制输入可以表示为：

v₁(τ)＝v₁ τ∈[kδ,(k+1)δ]

式中，时间段τ∈[kδ,(k+1)δ]被等分为δ^aver＝δ/(n-1)。将式(1)代入式(2-21)计算待定常数控制输入v＝[v₁,v₂₁,v₂₂,…,v_2(n-1)]^T，dim(v)＝n。应用分段常数控制输入算法对链式系统进行路径规划，控制输入v₁(τ)在整个时间段上始终维持不变，状态变量z₁(τ)的轨迹是一条连接位形z₁(k)和z₁(k+1)且斜率为v₁的直线；v₂(τ)在n-1段均分的时间上具有n-1维常数输入，故z₂(τ)的轨迹是一条分别以z₂(k)和z₂(k+1)为起点和终点，由n-1段等时间间距的直线首尾连接而成的折线，这表明状态变量z₂(τ)的路径是不光滑的。

令分段常数输入和的值在“0”与“1”之间切换，那么就有bang-bang控制输入：

与分段控制输入算法不同的是，bang-bang的控制输入始终在“0”与“1”之间切换，待定求解的系数不再是控制输入常数而是在每一段输入上所持续的时间段δ_i。bang-bang算法的最大优点在于控制简单，但存在问题仍然是规划出的路径依然局部不光滑，且控制输入对系统瞬时冲击较大。

算法描述：

三角函数切换算法集中了分段常数和bang-bang的优势，并且规划出的路径是完全光滑的；结合时间尺度变换技术平滑任一时间段上的过高速度输入且 不会在路径上引入不光滑的点。

将链式系统运动的时间等分为s段，在每一段上用半个周期的正弦曲线作为速度输入，以保证位移曲线在时间段切换处的平滑，那么系统的两个控制输入可以表示为：

其中，ω＝π/δ。式(3)数学结构类似于bang-bang控制，即系统的控制输入在“0”与“a_i sinωt”之间切换，但在时间段的划分上采用分段常数算法时间等分的方式。式(3)求解的是一组三角函数的常系数幅值[a₁,a₂,a₃,…,a_s]^T，该矢量的维数等于控制输入切换的次数。

三关节非完整机械臂的运动学模型可以变换为四状态的链式系统(三阶幂零两输入系统)，设初始位形为θ⁰＝[10°,10°,10°]^T，目标位形θ^f＝[30°,30°,30°]^T，利用式(3)作为输入，那么在奇数时间段上有速度输入：

式中，角频率ω＝π，代入式(2-21)积分，可以得：

式中，t∈[t_2i,t_2i+1]，i∈{0,1,2}。偶数时间段上的速度输入为：

代入链式系统积分可得：

式中，t∈[t_2j+1,t_2j+2]，i∈{0,1}。令k∈{1,2.3,4,5}，在整个积分区间上有：

式中存在5个待定系数，c₂和c₄可由下式确定，

实常数|a|＜1，则系数c₁和c₃为：

那么系数c₅为

c₅＝z₂^f-c₁-c₃-z₂⁰

链式空间的计算仿真结果如图1所示，首先四条路径是完全光滑的，其次路径的幅值没有出现过高的波动，这一特性有助于模型变换奇异问题的解决。

将图1映射到非完整机械臂的位形空间得到关节运动的轨迹，图2所示为三关节非完整机械臂的位移曲线和两部电机的实际控制输入曲线。控制输入切换次数为5，运行时间T＝5s。仿真结果显示在整个运动过程中电机2的转向更换一次，电机1的转向无变更。在实际应用中，伺服电机较少的转向更换次数可以减少传动系统带来的误差，提高运动控制的精度。三角函数切换算法的本质是将两个输入v₁和v₂切换作用于链式系统，通过非完整机械臂的反馈变换式将v₁和v₂映射到位形空间得到两部伺服电机的控制输入u₁和u₂，其中u₂表示为链式系统控制输入v₁和v₂的函数，而u₁仅与v₁相关。因此在1-2秒和3-4秒两个时间段上伺服电机1有速度输入u₁≠0，在其余时间段上的输入u₁＝0；而伺服电机2 在整个控制过程中始终有速度输入。伺服电机2与关节1相连接，故关节1的运动在整个过程中并未体现出算法的这种“切换性”，而关节2和关节3是由伺服电机1驱动的，因此仅在1-2秒和3-4秒这两段时间上关节2和关节3向目标位形运动。图2三角函数分段切换控制输入的运动路径(a＝0.29，d_a＝27.97°，t_p＝1)

算法改进：

虽然利用式(3)能够控制系统从初始位形θ⁰平滑地运动到目标位形θ^f，但在控制输入切换处的速度曲线并不光滑，如图2所示。为了平滑速度曲线，重新构建算法。

由链式系统数学模型的三角结构形式知，在控制输入[0,a_isinωt][a_i+1sinωt,0]的二次切换作用下，链式变量的运动在时间τ∈[(k+(i+1)/s)δ,(k+(i-1)/s)δ]上被分解为两部分，即[0,Δz₂,0,…,0]，[Δz₁,0,Δz₃,…,Δz_n]，其中 要使包含链式变量{z₃,z₄,…,z_n}的n-2个线性无关的方程有解，v₁必然最少经过n-2次切换输入，由式(3)知v₂最少需要n-1次切换输入，因此三角函数控制输入的切换次数最少为2n-3次，故链式系统路径规划的运动时间被等分的次数不低于2n-3，下面给出具体的证明：

定理1在控制输入

的作用下，两输入n维链式系统可以从初始位形z0运动到邻域内的目标位形z^f，其中系统的运动控制时间T最少等分2n-3次；

与式(3)类似，式(4)仍然是将链式系统运动的时间等分为s段，但在每一段上用一个周期的余弦曲线作为控制输入，这样做的好处是同时保证了位移曲线和速度曲线都是光滑的；下面给出算法定理1的数学证明；

证明：时间T被等分为2n-3次，每一个时间段长度为η＝T/(2n-3)，在奇数时间段上t∈[t_2i,t_2i+1]上(i∈{0,1,2,…,n-2})，等分的时间间隔表示为η＝t_2i+1-t_2i,，因此在奇数时间段上的式(4)可以表示为

式(5)中b_2i+1是待定系数，角频率ω＝2π/η，代入到式(21)逐步积分，

类似的，在偶数时间段上t∈[t_2j+1,t_2j+2](j∈{0,1,2,…,n-3})，等分的时间间隔表示为η＝t_2j+2-t_2j+1，因此算法式(4)在偶数段上有，

将式(7)代入到链式系统在时间t∈[t_2i+1,t_2i+2]上积分，得：

通过迭代计算式(6)和式(8)，得到系统运动到时间T的目标位形z^f，

式(9)中含有n个方程和2n-3个待定系数，将所有待定系数重新表示为两个系数矢量B_O＝[b₁,b₃,…,b_2n-3]^T和B_E＝[b₂,b₄,…,b_2n-4]^T，其中B_O和B_E分别称为奇数时间段系数矢量和偶数时间段系数矢量；由式(9)知B_E中n-2个元素满足，

$\underset{j=0}{\overset{n-3}{\Σ}}{b}_{2j+2}=\frac{z_1^f-z_1^0}{\mathrm{\η}}---\left(10\right)$

任意给定一组满足式(10)的B_E，当时，B_O中n-1个系数可以由式(9)中剩余的n-1个方程唯一确定；

证毕；

当时，有由式(9)知奇数时间段的系数矢量B_O无解；解决的办法是设置一个中间位形且满足系统的路径规划问题分为两个步骤，第一步先控制系统从初始位形z⁰运动到中间位形z^c，然后将中间位形z^c看成一个新的初始位形，控制系统运动到目标位形z^f；故当时，系统的路径就是以z^c为中间位形、首尾连接的两段路径组成。

以上显示和描述了本发明的基本原理和主要特征及本发明的优点。本行业的技术人员应该了解，本发明不受上述实施例的限制，上述实施例和说明书中描述的只是说明本发明的原理，在不脱离本发明精神和范围的前提下，本发明还会有各种变化和改进，这些变化和改进都落入要求保护的本发明范围内。本发明要求保护范围由所附的权利要求书及其等效物界定。