一种基于最短路径的线网划分方法与流程

本发明涉及一种基于最短路径的线网划分方法。

背景技术：

如何基于给定平面上的点集进行平面的划分是一个重要的数学问题，其在通信节点优化、物流配送、城市规划等重要领域都有着重要的实用价值。通过Voronoi图进行平面的划分是最为常见的形式。Voronoi图是数学上一种很重要的几何结构，在物理、化学、生物、工程等很多领域都作为重要的抽象模型表示方法得到了广泛的应用。给定平面上的离散点集P，其中每个点称为种子点，并对应一个划分单元。如果划分单元中任一点到本种子点距离小于到其他种子点的距离，我们称该平面划分为Voronoi剖分，对应的划分单元就称为Voronoi单元(Voronoi Cell)，1850年，Dirichlet在二次型研究中使用了2维和3维的Voronoi图。1908年，Georgy Voronoy定义并研究了一般n维空间的Voronoi图问题。为了寻求最优的空间划分结果，可以首先计算Voronoi图，然后不断将Voronoi单元的几何重心，作为新的种子点，重新计算Voronoi图，通过不断迭代，就可使得Voronoi单元的面积尽量相等。这就是重心Voronoi剖分(简称CVT)。香港大学的王文平等研究CVT的快速算法和基于GPU的加速,王晓宁等研究了三角网格上的CVT问题。

在实际应用中，比如在城市中分布电动车充电站时，一般会要求每个充电站的覆盖的区域的面积尽量相等，这就可以用Voronoi图的CVT方法来求解。但实际的城市中，充电站只能分布在街道边上，电动汽车也只能在街道上行驶，因此不能用传统的采用欧式距离计算Voronoi图的方法对平面进行划分。而是需要考虑实际道路情况，把平面的划分问题转化为在路网上的划分问题。而且在考虑到拥堵等实际情况，我们不必要求每个种子点覆盖的几何区域面积相等，而应该要求每个种子点覆盖的道路的总的加权长度相等。因此我们提出一种无向连通线网上的最优化的Voronoi划分问题。

技术实现要素：

本方法关注于在无向连通线网上的最优划分问题。首先给出了线网模型的描述与定义。面向需要解决的实际问题，本方法在进行线网模型的Voronoi图生成时，用线网上两点间沿着线网上节点间连通路线的最短路径距离代替了L2欧氏距离，因此这里所考虑的线网空间不具有凸空间的性质。本方法基于无向连通线网上最短路径算法，在给出一组随机分布的种子点后，计算得到当前线网上基于最短路径计算出的Voronoi单元；再将欧氏空间的Voronoi图CVT算法推广到无向连通线网上的Voronoi图上，通过迭代，使得线网上的每个种子点所对应的线网的加权长度尽量相等，从而得到了该线网模型的最优化划分。该方法可以有效解决城市道路上公共基础设施(加油站、充电站、卫生设施)等的分布、物流仓储节点分布等问题。

附图说明

下面结合附图和具体实施方式对本发明作进一步详细的说明:

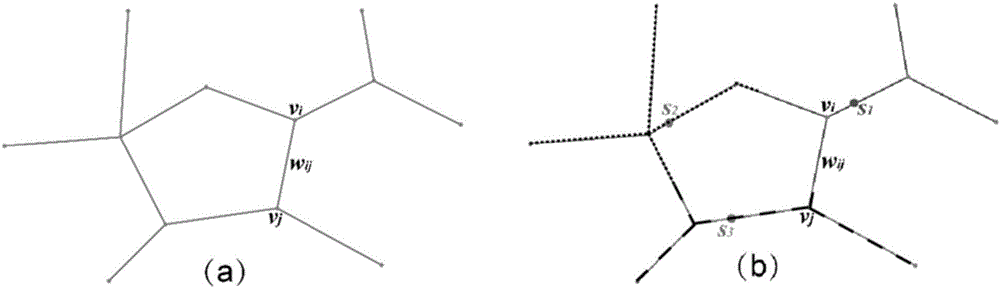
图1为线网模型和线网上的Voronoi图定义。其中(a)线网；(b)线网上Voronoi图,s1,s2,s3分别表示三个种子点，相应颜色标识了各个种子点对应的Voronoi单元。

图2为线网上Voronoi单元计算方法步骤示意图。

图3为应用示意图。其中包含北京市城区主要交通卫星图(上左)和六环以内主要交通道路的连接情况(上右，黑色方点为道路交叉点，直线为线网连接情况。一种初始充电站设置(中)，和本文方法经过35次迭代后的收敛结果(下)。

具体实施方式

线网模型定义：

线网模型表示了一组顶点以及顶点间的连接关系，在路径规划等方面有着广泛的应用。我们定义N维空间上的线网G＝(V,E)，如图1(a)所示。其中顶点集合为：

边集合为：

中一条有限长连续曲线γ_ij以v_i和v_j端点且不经过

在最短路径问题中，一般还为线网的每条边(v_i,v_j)∈E赋予权重w_i,j。从顶点v_i到v_j路径上依次经过的边的权重之和称该路径的权重。从顶点v_i到v_j具有最小权重的路径称为顶点v_i到v_j的最短路径，相应的权重称为顶点v_i到v_j的最短距离，记为d_i,j。若顶点集合中任意两点间均存在路径，则称线网是连通的，否则线网是非连通的。若边是有方向的，即(v_i,v_j)和(v_j,v_i)表示不同的有向边，则称线网为有向线网，否则为无向线网。对于无向线网，可认为(v_i,v_j)和(v_j,v_i)表示相同的边且有w_i,j＝w_j,i。

线网上的Voronoi图

本方法考虑无向连通线网上的Voronoi图问题，定义N维连通线网G＝(V,E)上的线网空间Ω_G为:

在曲线γ_ij上且(v_i,v_j)∈E}. (3)

记d_G(p₁,p₂)为线网空间Ω_G上两点p₁,p₂间的距离度量，w(p₁,p₂)为同一曲线上两点p₁,p₂间权重。给定Ω_G上的离散点集点s_k对应的Voronoi单元定义为：

称为线网空间Ω_G的一个Voronoi划分。图1(b)表示了一个线网上的三个种子点确定的Voronoi单元。

线网的重心

对于线网上的Voronoi剖分，我们也希望每个Voronoi单元的“面积”——权重之和——尽量相等，比如在实际应用中，我们希望均匀地设置充电站，使得每辆电动汽车到其最近的充电站所需的时间尽量相等；再如，我们希望在公园中摆放垃圾桶，使得每个游客到离其最近的垃圾桶所走路程尽量相等。

为此，给定无向连通线网G＝(V,E),以及线网空间Ω_G上的概率密度函数ρ,对于给定的m个种子点对应的Voronoi剖分我们定义每个Voronoi单元的“重心”为

其中，E_k为子线网G_k的边集合。

无向连通带权重线网上的Voronoi图剖分的计算方法

给定无向连通线网G＝(V,E)，权重W以及线网空间Ω_G上的m个种子点线网G上的Voronoi剖分，就是要计算出每个种子点对应的Voronoi单元计算无向连通线网上的Voronoi图的关键在于计算出线网中任意两点间最短路径的长度，即定义在线网空间上任意两点的距离。为此，我们先考虑将种子点集加入线网G＝(V,E)，并更新得到线网G_S＝(V_S,E_S)以及对应的权重W_S，然后计算线网G_S上顶点间的最短路径长度。接下来，就可以计算G_S＝(V_S,E_S)中顶点所属Voronoi单元以及边的分割点。最后根据分割点形成线网上的Voronoi剖分。具体方法如下：

(一)将种子点集加入线网G＝(V,E)，并更新得到线网G_S＝(V_S,E_S)以及对应的权重W_S：S中的每个点s,假设s所在边为(v_I,v_j)，则有：

E_S＝E_S∪{(s,v_i),(s,v_j)}\{(v_i,v_j)},W_S(s,v_i)＝w(s,v_i) (6)

W_S(s,v_j)＝w(s,v_j),W_S(v_i,v_j)＝+∞,W_S(s,s)＝0 (7)

(二)获取新的最短路径。本方法仅考虑非负权连通线网的情况。对于非负权连通线网，我们遍历线网的每个顶点，采用Dijkstra算法计算该顶点到其余顶点的最短路径，得到任意两顶点间的最短路径。

(三)计算Voronoi图：

给定无向连通线网G＝(V,E)，Voronoi种子点集计算点集S关于线网空间Ω_G一个Voronoi划分即是在线网G_S＝(V_s,E_s)及其线网空间上确定V_s中每个顶点所属的Voronoi单元，以及每条边E_s上的点所属的Voronoi单元。

3.1计算V_s中顶点的所属Voronoi单元

定义为线网空间到Voronoi种子点集S的子集的映射，表示线网空间中每个点和所属Voronoi单元的种子点集合的对应关系。

由于V_s中的点分为两部分——线网G中的顶点集V和Voronoi种子点集S。对于Vor(s)＝{s}；对于有，

3.2计算E_s中边上点的所属Voronoi单元

如果一条边的一个端点到其所属一个Voronoi单元的种子点的最短路径经过该边，则该边上任意一点都属于该Voronoi单元。否则，该边上的点可能属于不同的Voronoi单元。所以采用如下方法判断其属于哪个Voronoi单元：

若(v_i,v_j)∈E_S，记

S_ij＝Vor(v_i)∩Vor(v_j)， (9)

d_i为v_i到Vor(v_i)中种子点的距离，d_j为v_j到Vor(v_j)中种子点的距离，

(i)若|d_i-d_j|＝w_i,j，则对曲线γ_ij上任意一点p(不含端点v_i,v_j)，有

Vor(p)＝S_ij (10)

(ii)若|d_i-d_j|≠w_i,j，曲线γ_ij上存在唯一分割点p_c，使得Vor(p_c)＝Vor(v_i)∪Vor(v_j)，且曲线γ_ij上p_c到端点v_i的权重为：

w(p_c,v_i)＝(w_i,j+d_j-d_i)/2。 (11)

以上两式的证明如下：

证明：先证明(i)。不失一般性，假设

d_j＝d_i+w_i,j。 (12)

对显然有于是有

由于d_j为顶点v_j到所有种子点的最小距离，于是有s′∈Vor(v_j),即

于是有，

S_ij＝Vor(v_i)。 (15)

根据(13)，由最短路径的子路径性质可知，从v_j到s′的最短路径经过边(v_i,v_j)。由最短路性质知，对曲线γ_ij上任意一点p(不含端点v_i,v_j)，p属于s′所在Voronoi单元，于是有

考虑以及曲线γ_ij上任意一点p(不含端点v_i,v_j)，我们有

又由最短路性质知

又由(12)知

由(17)～(20)有，

由(21)知，对有

又由闭合性知，

由(15)(16)(22)(23)便有Vor(p)＝S_ij。(i)得证。

再证明(ii)。不失一般性，假设d_i<d_j，则必有

d_j<d_i+w_i,j。 (24)

否则，若d_j>d_i+w_i,j，则我们为v_j到种子点间找到条更短的路径，这与已知d_j是v_j到种子点的最短距离矛盾。对于曲线γ_ij上任意一点p，由闭合性知，

如图2所示，考虑k≠l。不失一般性，假设

则p到s_k的最短路径必先直接经过端点v_i再到达s_k。若不然，p到s_k的最短路径先经过端点v_j再到达s_k，有

又由d_j是v_j到种子点的最短距离知，

由(27)(28)和最短路径的定义可知，

这与(26)矛盾。此时，由(25)(26)式可知，

由(25)(30)知此时有

Vor(p)＝Vor(v_i)。 (31)

由于曲线γ_ij是连续的曲线，曲线上点p从一个端点到另一个端点连续变化过程中，p到所有种子点的最小距离也连续变化。又由(24)知，该最小距离先单调递增再单调递减。于是曲线γ_ij上存在唯一分割点p_c，并且在该分割点处有

再由(31)(32)便知，

Vor(p_c)＝Vor(v_i)∪Vor(v_j)。 (33)

由于此时p_c到s_k的最短路径经过端点v_i，于是有

同理，有

又由于

w_i,j＝w(p_c,v_i)+w(p_c,v_j)， (36)

将(34)～(36)代入(32)便得到(11)。

证毕

对E_s中的任一条边(v_i,v_j)，根据以上方法即可判断该边是否存在分割点，若存在分割点，(11)式给出了分割点的位置。记所有这样的边界分割点集合为C。

由Vor的定义以及线网上Voronoi单元的定义可知,

考虑单元内的顶点以及分割点构成的子线网G_k＝(V_k,E_k)，则有

这说明，线网空间上的Voronoi划分对应着线网G_S的一个划分

(四)最后使用Lloyd算法中的迭代方式来求解给定区域的重心Voronoi剖分，它通过不断迭代地构建Voronoi剖分和更新种子点位置。给定种子点个数m，区域Ω，以及定义在Ω上的概率密度函数ρ，主要过程如下:

1)随机选定m个初始种子点

2)根据种子点计算关于区域Ω的Voronoi剖分

3)计算步骤2)中每个Voronoi单元的重心，得到新的种子点集

4)如果新的种子点集满足给定的收敛准则(一般使用新的点集与上一步点集的平均距离是否小于给定阈值的方法来判断，该阈值可设为0.1倍单位长度)，则算法结束，否则，执行步骤2。

这种迭代方式已被Kieffer等人证明具有局部收敛性。这样所得到的Voronoi剖分，就是该线网模型在给定点集作为种子点的情况下的最优划分。

方法应用

随着电动汽车成为越来越多人的选择，城市交通中对电动汽车充电站的需求也日益增加，如何规划充电站的位置，使得用户能尽快找到就近的充电站以及提高每个充电站的利用率成为设计者需要考虑的问题。这里以北京市六环以内的主要交通道路为例,利用本方法演示如何确定50个充电站位置。图3中显示了通过北京地图上的道路连接情况生成的线网(1034个顶点，1801条边，边权重为相应道路的长度)和放置50个充电站的最终优化结果。通过该应用验证了本方法可以有效解决路网上的节点均匀分布问题。