基于生存模型对资产证券化资产池进行评级的方法与流程

本发明涉及资产评级技术领域，更具体地说，特别涉及一种基于生存模型对资产证券化资产池进行评级的方法。

背景技术：

1、资产证券化，例如以民用住房贷款为抵押的资产证券化；2、资产抵押，譬如汽车贷款、设备贷款为主的资产证券化；3、抵押贷款债权，为目前主要的三大规模性融资手段，上述三种融资方式可以帮助银行来管理银行的资产负债表，也可以使金融企业将不可能流动性资产转化为流动性资产。资产证券化可以使金融机构获得更为廉价的资金，能够使金融机构的融资手段更为丰富。

发行机构在进行资产池评级的时候，往往需要根据资产池的历史数据和特性决定资产池的违约率来对证券化产品进行评级。那么，如何提供一个能对资产池，特别是包含海量资产数据的资产池(几百条到百万条)进行准确的、有效的评级，就显得尤为重要。

技术实现要素：

(一)技术问题

在资产池评级过程中面临如下挑战：

1、目前普遍使用的log-normal分布模型的局限性：

log-normal分布不能完善的描述损失率的分布，以及在方差的选择上缺乏可信度。另外，该模型在信息量较低时是相对高效的，但是难以在此基础上延伸。Log-normal分布模型具有较强的参数化假设，不 能完善的描述真实损失率的分布，特别是在多峰和厚尾的情形下会偏离真实情况较多，应用于损失率预测的场景时会造成对风险的估计不足。另外，该模型适用于在历史数据较少时相对高效的进行模拟，但难以推广用于更加丰富的数据。

2、违约率分析、评级过程的速度不能胜任海量数据计算：

金融机构的资产池往往是海量数据。数据级别在百万、千万条记录。如何在非常短的时间内进行海量数据的评级也是一个巨大的挑战。

(二)技术方案

本发明提供了一种基于生存模型对资产证券化资产池进行评级的方法，该方法具体包括：

步骤一、构建生存模型：

贷款到违约距离时间为T；

拥有累积概率密度函数为：

F_T(t)＝P(T≤t):R→[0，1]

概率密度函数为：

贷款到t时刻不违约概率计算的生存函数为：

S(t)＝1-F_T(t)

在时刻t处一段极小的时间内发生违约概率密度计算的危险函数为：

由上述函数可得：

即：

步骤二、进行违约模拟：

在获得S(t)函数之后，使用蒙特卡洛模拟方法对资产池在时间序列上进行逐笔的违约模拟并获得评级，其中S(t)为蒙特卡洛抽样提供概率基准。

优选地，通过历史数据拟合h(t)来获得S(t)；

以拟合方法获得h(t)函数：

在生存模型中的观察时间和违约记录，并确定函数：

其中T_i是生存时间，C_i是观察时间(贷款到期时间)；

如果发生违约，记Δi＝1，否则记Δi＝0；

对于存续期内未发生违约的贷款样本i，在时间轴t上满足联合概率为：

P(C_i＝t_i)P(T_i＞t_i)

对于存续期内发生违约的样本i，在时间轴上满足联合概率为：

P(C_i＞t_i)P(T_i＝t_i)

静态池中的所有资产，似然函数为：

其中P(T_i＝t_i)＝f(t_i)＝h(t_i)S(t_i)，因此得出如下函数：

其中G(t_i)和g(t_i)为观测时间C_i的CDF和PDF，对G(t_i)和g(t_i)进 行常数化，因此得出如下函数：

其中对数似然函数为：

通过极大似然估计取得h(t)的估算值，确定在极短时间内发生违约的概率不因观测时间点而改变，即h(t)＝λ即S(t)＝e^-λt。

优选地，通过历史数据拟合h(t)来获得S(t)；

通过总违约数量除以总暴露时间来估计h(t)，结合Weibull模型得到如下函数：

h(t)＝λα(λt)α-1，其中α,λ>0；

通过分段求得h(t)模拟值，并采取MCMC方法拟合其曲线。

(三)有益效果

本发明提供了一种基于生存模型的信贷资产证券化资产池评级的方法，该方法可以利用生存模型，更为准确、有效的对海量资产的资产池进行评级。与现有技术相比，本发明利用了一种新的生存模型来对资产池进行评级，该生存模型旨在探寻违约事件的(无条件的)发生概率，在数据缺乏，结构不完整的情况下构建可能的模拟方法。生存模型在进行时间序列分析时(比如在希望了解时间对违约率的影响)以及用于蒙特卡洛模拟时表现非常优秀。基于该模型，本发明还提供了一种与其对应的硬件设备，该硬件设备对数据的存储方式、访问效率以及算法都进行了极大程度的优化，使得评级过程中对海量数据的处理、访问和存储性功能都极大的提高。

附图说明

图1为本发明中危险函数的估算和非线性曲线的拟合对比图；

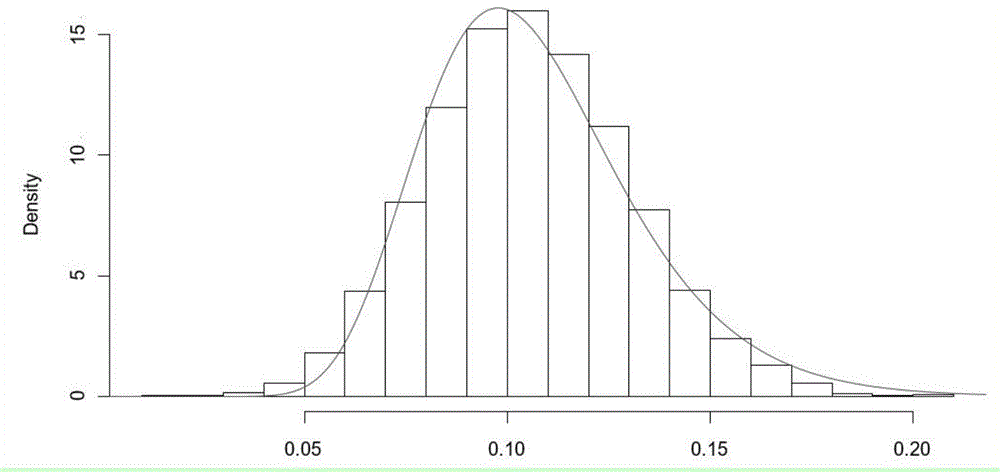
图2为本发明中10000次一年期债券损失率(Loss Rate)估算与log-normal分布的对比图；

图3为本发明的基于生存模型的信贷资产证券化资产池评级模型的流程图。

具体实施方式

下面结合附图和实施例对本发明的实施方式作进一步详细描述。以下实施例用于说明本发明，但不能用来限制本发明的范围。

在本发明的描述中，除非另有说明，“多个”的含义是两个或两个以上；术语“上”、“下”、“左”、“右”、“内”、“外”、“前端”、“后端”、“头部”、“尾部”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本发明的限制。此外，术语“第一”、“第二”、“第三”等仅用于描述目的，而不能理解为指示或暗示相对重要性。

在本发明的描述中，需要说明的是，除非另有明确的规定和限定，术语“相连”、“连接”应做广义理解，例如，可以是固定连接，也可以是可拆卸连接，或一体地连接；可以是机械连接，也可以是电连接；可以是直接相连，也可以通过中间媒介间接相连。对于本领域的普通技术人员而言，可以具体情况理解上述术语在本发明中的具体含义。

请参考图1至图3，其中，图1为本发明中危险函数的估算和非线性曲线的拟合对比图；图2为本发明中10000次一年期债券损失率(Loss Rate)估算与log-normal分布的对比图；图3为本发明的基于生存模型的信贷资产证券化资产池评级模型的流程图。

在附图的流程图示出的步骤可以在诸如一组计算机可执行指令的计算机系统中执行。并且，虽然在流程图中示出了逻辑顺序，但是在某些情况下，可以以不同于此处的顺序执行所示出或描述的步骤。

生存模型

本发明提供了一种基于生存模型对大数据容量的资产池进行评级的方法，在本发明在生存模型中，如果需要研究一笔资产何时违约，那么首先设定贷款到违约距离时间为T，T为一个随机变量。

拥有累积概率密度函数(CDF)为：

F_T(t)＝P(T≤t)：R→[0，1]

概率密度函数(PDF)为：

定义生存函数(survival function)：S(t)＝1-F_T(t)

即该贷款到t时刻不违约的概率。

定义危险函数(hazard function)，危险函数为在时刻t处一段极小的时间内发生违约的概率密度。

因此结合上述生存函数以及危险函数

由上述公式可得：

在实际操作中，由于观测时间的限制，一般无法获得完整的违约分布f_T(t)，因此，本发明通过历史数据拟合h(t)来获得S(t)。在获得S(t) 之后本发明使用蒙特卡洛模拟的方法来对一个资产池在时间序列上进行逐笔的违约模拟，S(t)将为蒙特卡洛抽样提供概率基准。

利用历史数据对h(t)的拟合方法如下：

对于生存模型为了估计h(t)，首先要得到该模型的似然函数，即资产池内样本生存时间的联合概率分布。在生存模型中对于一笔资产需要如下数据：观察时间以及违约记录，并将其记为：

上述公式中，T_i是生存时间，C_i是观察时间(贷款到期时间)。如果发生违约，记Δi＝1，否则记Δi＝0。对于存续期内未发生违约的贷款样本i，在时间轴t上满足联合概率：

P(C_i＝t_i)P(T_i＞t_i)

而在存续期内发生违约的样本i，在时间轴上满足联合概率：

P(C_i＞t_i)P(T_i＝t_i)

因此，对于静态池中的所有资产，似然函数为：

其中P(T_i＝t_i)＝f(t_i)＝h(t_i)S(t_i)，因此得到如下公式：

其中G(t_i)和g(t_i)是观测时间C_i的CDF和PDF，在对h(t_i)极大似然值不产生影响时可以简化为常数，得到如下函数：

其对数似然函数为：

对参数进行假设

对h(t)进行假设，并通过极大似然估计取得h(t)最可能的值。最简单的参数模型指数模型(exponential)，该模型中我们假设在极短时间内发生违约的概率不因观测时间点而改变，即h(t)＝λ，因此S(t)＝e^-λt。

此时似然函数演变为：

为取得λ的最大可能值，对λ求导并令结果等于0：

等式化简为：

从上式可以看出，我们可通过总违约数量除以总暴露时间来估计h(t)，其中总暴露时间为月未偿还笔数乘以每月观测时间累加得到。

指数模型的优势在于易于获得数据，所需计算量较小，但指数模型也因此受到许多因素限制：缺乏调控风险率与贷款时间的杠杆。因此，本发明可以进一步考虑采用Weibull模型，即：h(t)＝λα(λt)α-1，其中α，λ＞0。

Weibull模型增加了变量α可以调控风险函数随时间(单调地)增长/减少，当α＝1时该模型为指数模型，当α＞1时，风险函数随时间的增长而增长。实际操作中Weibull分布的似然函数难以求最大 似然估计值。通过分段求得h(t)模拟值，并采取MCMC或其他方法拟合其曲线。

由图1可以看到Weibull获取的数值分布对该静态池的数据的拟合具有较高的合理程度(后几个月由于样本较少偏离曲线)。

实现步骤

如果需要评估一笔组合资产(X，W)，其中X∈Rn为到期时间，W∈Rn是权重，可以使用蒙特卡洛模拟算法来采样：

u～U(0，1)，Amount～LN(μ，σ2)，

其中μ，σ2是静态池中每笔贷款的均值与方差。t～U(0，1)，这里t为还贷时间除以贷款到期时间的分布，规定还款分布均匀，因此可以将其替换为其他分布。

对i＝1，2，...，n，如果u_i＞S(X_i×t_i)，则记Δi＝1，否则记Δi＝0，于是获得损失率：

重复以上步骤10000次，得到损失率的经验分布。这里假设资产池中的资产没有相关性。如果已知资产池中的资产具有具有某种相关性(设相关矩阵为∑)，则将第一步可改为采样u0～MN(0，∑)，取u＝Φ(u0)，其中Φ(.)为正态分布的CDF。对于指数分布，对于Weibull分布，

以最简化的例子而言，假设有10笔贷款资料(上限均为12个月)

根据上述表格，使用危险函数测得总未偿数量4，总暴露时间是

3+5+11+8+12*6＝99，因此h(t)＝4/99

那么贷款生存时间-概率的分布为e-^(4/99)t，t为时间。

损失暴露的经验分布为X＝800,1300,2000,5000(各1/4)。

回收率的经验分布为R＝0(p＝3/4)，3/4(p＝1/4)

图2显示上述模型使用蒙特卡洛模拟的结果与log-normal方法得到的结果相比较。由此验证：在资产池足够大的时候，log-normal分布与本发明模拟的结果非常符合。

本申请可以对海量资产的资产池进行评级，快速的进行计算，一般在5分钟内，能完成百万条数据级别的评级。

本发明的实施例是为了示例和描述起见而给出的，而并不是无遗漏的或者将本发明限于所公开的形式。很多修改和变化对于本领域的普通技术人员而言是显而易见的。选择和描述实施例是为了更好说明本发明的原理和实际应用，并且使本领域的普通技术人员能够理解本发明从而设计适于特定用途的带有各种修改的各种实施例。