一种电力‑天然气区域综合能源系统的稳态分析方法与流程

本发明涉及能源互联网、综合能源系统、天然气系统、智能电网领域，特别涉及一种电力-天然气区域综合能源系统稳态分析方法。

背景技术：

能源是国家发展的基础，近年来，随着能源互联网、综合能源系统等理念的不断推广，能源系统的发展呈现多样化、智能化、信息化趋势。在由电力、天然气和热力系统共同构成的区域综合能源系统中，能源耦合紧密，互补互济，可实现能源的梯级利用和协同优化。结合不同形式能源的供需特性，充分考虑其协同作用与彼此之间的相互影响，是提高综合能源系统中能源利用效率的关键，一方面，不同能源具有互补特性，在经济性方面尤其明显，多能协调可以有效减少能源系统整体经济成本，并具有削峰、移峰的潜力；另一方面，不同能源系统可通过能源耦合对彼此进行支撑，提高供能系统稳定性。其中，天然气系统具有易存储、绿色清洁、安全可靠等特点；同时，随着燃气轮机、热电联产(Combined Heat and Power，CHP)等技术的广泛应用以及对能源集线器(Energy Hub，EH)技术不断的研究，天然气在能源系统中的重要性愈加显著。而能源系统彼此之间耦合不断加强，需要深入研究其交互影响和协同优化方法。

天然气系统(Natural Gas System，NGS)与电力系统存在一定的相似性，在稳态建模和潮流分析特性等方面尤其明显，因此可以借鉴电力系统已有的分析思路开展研究。天然气系统与电力系统的主要差异是：前者具有大规模储存特性且对气质有特殊要求，对这种差异性的分析往往是提高综合能源系统供能质量的关键。天然气本身是由多种气体成分构成的，其气质在系统引入其他种类天然气或出现新的注气点后会发生一定变化。天然气系统的网络状态受气质、结构、压力等因素影响，当这些因素发生改变时，传统的天然气系统分析方法将难以适用。本发明将主要讨论“天然气气质变化”和“注气点引入”这两个因素对天然气系统本身以及与之存在耦合关系的区域综合能源系统其他部分的影响，而如何构建适用的天然气系统分析模型与综合稳态求解框架是其中的关键。

现有技术中至少存下以下缺点和不足：目前，相关领域的研究者对综合能源系统的讨论主要集中在跨区级，此外，相关研究忽略了天然气网络状态特性，将其假定为稳定不变的。这些方法的局限在于，上述研究对于以配电系统(具有三相不平衡潮流特性)、配气系统(具有低压天然气网络特性)为主体且能源耦合密切的区域级综合能源系统讨论相对较少，同时，由于电力转天然气技术(Power to Gas，P2G)等技术的应用，天然气系统网络状态会发生改变(如天然气气质改变与引入新的注气点)，传统的分析方法不再适用，具有一定的局限性。

技术实现要素：

针对以上问题，本发明提出了一种电力-天然气区域综合能源系统的稳态分析方法，本方法将区域综合能源系统中电力系统与天然气系统协同考虑，结合能源耦合分析，有利于探究天然气系统的变化对其自身以及与之耦合的系统的影响，是提高综合能源系统供能质量、降低能源系统用能成本的关键。

本发明提出了一种电力-天然气区域综合能源系统的稳态分析方法，该方法包括以下步骤：

步骤(1)、对电力-天然气区域综合能源系统中的天然气系统进行建模与求解；具体包括：

读取天然气网络信息、分布式发电单元信息和能量交互信息；

分析天然气网络特征，构建节点导纳矩阵；

对于天然气系统中的压力已知节点，不同压力等级的天然气流量公式如下所示：

(a)式适用于0-75mbar压力范围，(b)式适用于0.75-7.0bar压力范围，(c)式适用于大于7.0bar压力范围的情况；

其中，i与j分别为天然气管道首末节点，q_ij为标准状况下的管道流量，p_i与p_j分别为表节点压力，D与L为管道的直径和长度，SG为相对密度，f为摩擦系数，Z为计算常数，T_n与p_n为标准状况下的温度与压力；

步骤(2)、对天然气系统进行节点压力-负荷灵敏度分析，令天然气节点压力-负荷灵敏度矩阵其中，p为压力，l为负荷；

步骤(3)、基于天然气系统信息与能源交互信息，构建以能源集线器为核心的能源耦合环节建模以及能量转换分析，具体包括以下处理：

读取外界环境参数与分布式产能单元信息；

根据当前状态，分析能源集线器设备类型、能源交互信息与结构特征；

构建能源集线器转换矩阵C与方程L＝CP，分析耦合设备交互方式；

求解x_e和x_g改变值：对耦合设备能量交互进行数值转换；

整合能源交互信息，求解能源集线器方程；

步骤(4)、对电力系统稳态求解，在回代的过程中，以配电网的始端电压和末端负荷作为已知条件，由负荷功率逐步逐段计算线路各部分的功率损耗，进而推算始端功率；在前推的过程中，以始端电压和上述过程求得的始端功率为已知条件，以电压降落为所求量，从线路始端向末端进行计算，进而求得各个节点的电压。前推与回代过程重复迭代，在满足收敛条件后停止，并输出结果；若电力系统计算结果均在系统的合理运行区间，则计算结束输出结果；否则，返回能源耦合环节并对其进行调整，通过循环迭代，保证电力系统运行在合理范围之内；

步骤(5)、结合天然气系统与电力系统的综合求解信息，构建电力-天然气区域综合能源系统稳态分析综合求解模型，首先读入外界环境信息；根据天然气系统初始化部分以及天然气系统求解部分，输出天然气系统待求变量以及天然气系统压力-负荷灵敏度矩阵；分析以能源集线器为核心的能源耦合环节，对耦合设备能量交互进行数值转换；最后，将上述信息代入到电力系统计算过程，若电力系统计算结果均在系统的合理运行区间，则计算结束输出结果；否则，返回能源耦合环节并对其进行调整，通过循环迭代，保证电力系统运行在合理范围之内；从而获得天然气系统网络状态改变对其自身以及区域综合能源系统的影响。

1.如权利要求1所述的一种电力-天然气区域综合能源系统稳态分析方法，其特征在于，其中对电力-天然气区域综合能源系统中的天然气系统进行求解的过程，具体包括以下步骤“

初始化：根据天然气网络状态确定天然气系统求解所需的相关参数；

利用图论思想，构建展现网络拓扑信息的节点与支路的关联矩阵A，其元素A_ij如下定义：

对天然气系统进行描述，公式如下：

其中，为已知节点压力，为未知节点的压力，表示根据天然气流量公式确定的管道流量方程；为净负荷量，与分别某节点的天然气注入量和消耗量。上述方程表征含义即天然气流入某节点的量等于流出该点的量加上该点的净负荷量；此时，将天然气潮流问题进一步表述为根据已知信息求取压力已知节点的流量以及流量已知节点的压力；

借鉴电力系统潮流分析中的牛顿法对其进行求解，将误差方程F表示为：

构建天然气系统的雅可比矩阵J如下所示：

其中，p_i与p_j代表节点压力，q_ij为标准状况下的管道流量；A₁为排除压力已知节点之外的缩减关联矩阵，A₁^T为A₁的转置矩阵；为未知节点的压力。

通过构造雅可比矩阵与牛顿-拉夫逊方法的应用，对天然气系统压力值进行反复迭代，直至误差方程的值小于收敛标准，输出潮流结果。

本发明所运用的分立求解方法，对电力-天然气区域综合能源系统整体分析，针对“以气定电”的运行场景，探究天然气系统网络状态改变对其自身以及区域综合能源系统的影响，为能源互联网背景下的能源互济与相互影响分析提供一定的理论基础。

附图说明

图1为本发明提供的电力-天然气区域综合能源系统稳态求解流程图；

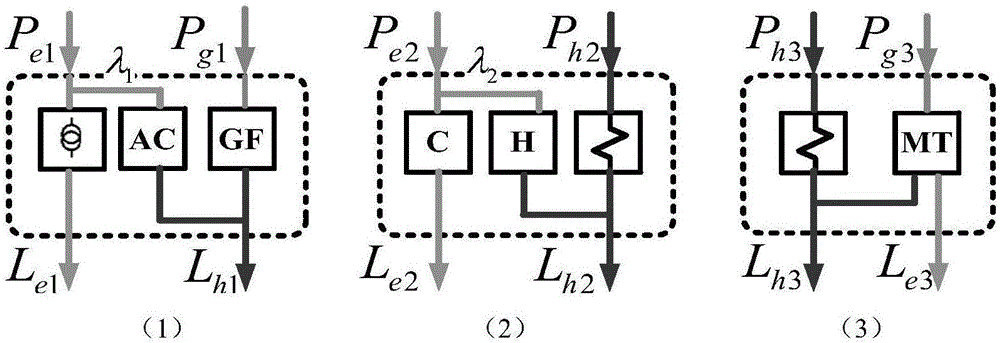
图2为三种典型能源集线器结构示意图，附图标记：(1)、I型能源集线器、(2)、II型能源集线器、(3)、III型能源集线器；

图3为电力-天然气区域综合能源系统示意图；

图4为天然气压力-负荷灵敏度矩阵示意图；

图5为电力系统各相电压幅值在天然气系统注入不同气体情况下的变化结果曲线示意图。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明实施方式作进一步地详细描述。

参见图1，本发明的电力-天然气区域综合能源系统稳态求解思路主要分成四个部分，首先，对天然气系统网络状态变化进行分析，判断是否有注气点或气质的改变，根据其变化调节天然气系统求解模型，并完成天然气系统初始化设置，具体包括天然气的相对密度、节点-支路关联矩阵、摩擦系数等参数；其次，通过牛顿法对天然气系统潮流方程进行求解，并根据其结果求得天然气灵敏度矩阵；再次，结合天然气系统相关信息，分析能源耦合环节能量交互方式并进行数值求解；最后，将上述信息代入到电力系统计算过程，对电力系统稳态求解，若电力系统计算结果均在系统的合理运行区间，则计算结束输出结果；否则，返回能源耦合环节并对其进行调整，通过循环迭代，保证电力系统运行在合理范围之内；结合综合求解信息，构建电力-天然气区域综合能源系统稳态分析综合求解模型，探究天然气系统网络状态的改变对其自身以及与之耦合的电力系统影响。

步骤1、对电力-天然气区域综合能源系统中的天然气系统进行建模与求解

步骤2、对天然气系统进行节点压力-负荷灵敏度分析；

步骤3、基于天然气系统信息与能源交互信息，构建以能源集线器为核心的能源耦合环节建模以及能量转换分析；

步骤4、对电力系统稳态求解；在电力系统的稳态求解中，主要应用前推回代的方法。具体来说，在回代的过程中，以配电网的始端电压和末端负荷作为已知条件，由负荷功率逐步逐段计算线路各部分的功率损耗，进而推算始端功率；在前推的过程中，以始端电压和上述过程求得的始端功率为已知条件，以电压降落为所求量，从线路始端向末端进行计算，进而求得各个节点的电压。前推与回代过程重复迭代，在满足收敛条件后停止，并输出结果。

步骤5、构建电力-天然气区域综合能源系统稳态分析综合求解模型，在此基础上，探究天然气系统网络状态改变对其自身以及区域综合能源系统的影响。获得天然气系统网络状态改变对其自身以及区域综合能源系统的影响。在该步骤中，首先读入外界环境信息(例如分布式发电单元的出力情况)；根据天然气系统初始化部分以及天然气系统求解部分，输出天然气系统待求变量(例如管道流量与节点压力)以及天然气系统压力-负荷灵敏度矩阵；分析以能源集线器为核心的能源耦合环节，对耦合设备能量交互进行数值转换；最后，将上述信息带入到电力系统计算过程，若电力系统计算结果均在系统的合理运行区间，则计算结束输出结果；否则，返回能源耦合环节并对其进行调整，通过循环迭代，保证电力系统运行在合理范围之内。

所述步骤(1)具体为：

天然气系统普遍主要存在两种节点，一种是压力已知节点，一般为气源点，其压力固定且已知，经过该点的流量为待求量，类似于电力系统中的平衡节点；另一种是流量已知节点，一般为负荷节点，其压力为待求量，类似于电力系统中的PQ节点(有功功率P和无功功率Q给定、节点电压与相位待求的节点)。本步骤借鉴电力系统较为成熟的稳态分析思路，对天然气系统进行建模与求解，并考虑天然气系统的网络状态变化(如天然气气质改变与引入新的注气点)。从天然气系统建模的角度，天然气气质的改变主要影响其相对密度；注气点的引入往往需要铺设相应的管道连接至天然气系统，这意味着在其区域范围，天然气系统的节点-支路关联矩阵发生改变，同时也会引起相对密度的变化。

天然气系统的支路可以分为不含压缩机支路与含压缩机支路两种。天然气管道两端存在压力降，管道流量为其待求量，与管道两端压力相关，其公式与管道压力等级和相应的网络参数有关联。天然气系统在运行中满足流体力学质量守恒定律与伯努利方程，基于一定假设的不同压力等级的天然气流量公式如下所示：

其中，(a)式适用于0-75mbar压力范围，(b)式适用于0.75-7.0bar压力范围，(c)式适用于大于7.0bar压力范围的情况。i与j分别为天然气管道首末节点，q_ij为标准状况(Standard Temperature and Pressure，STP)下的管道流量，p_i与p_j代表节点压力，D与L为管道的直径和长度，SG为相对密度，f为摩擦系数，Z为计算常数，T_n与p_n为标准状况下的温度与压力。在区域综合能源系统中，由于天然气压力等级不高，往往需采用式(a)或(b)所给的低压场景计算公式。

在天然气系统的潮流求解中，首先利用图论思想，通过构建节点与支路的关联矩阵A展现网络拓扑信息，其元素A_ij如下定义：

A₁为排除压力已知节点之外的缩减关联矩阵，这种方法较为清晰简便且方便编程调用。

根据天然气系统的压力等级，确定上述天然气流量公式；天然气系统可通过如下式子进行描述：

其中，为已知节点压力，为未知节点的压力，表示根据天然气流量公式确定的管道流量方程；为净负荷量，与分别某节点的天然气注入量和消耗量。上述方程表征含义即天然气流入某节点的量等于流出该点的量加上该点的净负荷量。此时，天然气潮流问题可以表示进一步表述为根据已知信息求取压力已知节点的流量以及流量已知节点的压力。

上述式子是典型的非线性方程，对于给定的压力初值，其左右两边往往并不相等，此时可借鉴电力系统潮流分析中的牛顿法对其进行求解，其误差方程F为：

应用牛顿法的关键是求导其雅可比矩阵，经推导，天然气求解方程的雅可比矩阵可以统一写成上式的形式，通过构造雅可比矩阵与牛顿-拉夫逊方法的应用，对天然气系统压力值进行反复迭代，直至误差方程的值小于收敛标准，输出潮流结果。雅可比矩阵J如下所示：

其中，p_i与p_j代表节点压力，qi_j为标准状况下的管道流量。

运用牛顿法求解天然气网络潮流具有构造清晰、适用性强等特点，该种方法需要对所求系统有一定的了解，给出合理的初值。经多种算例验证，该求解模型较为高效、稳定。

对于含有压缩机的支路，则采用如下方程进行分析：

R_kij＝p_j/p_i

其中，H_kij表示压缩机所需功率，B_k为与压缩机温度、效率、绝热指数相关的参数，f_k为流经压缩机管道的流量；R_kij为压缩比。压缩机运行需要额外的功率，当该部分功率由天然气通过燃气轮机提供时，所消耗的天然气流量为方程中的τ,α,β,γ为燃气轮机燃料比率系数；压缩机运行所需功率也可由电网提供。

本发明采用节点法列解天然气系统的潮流方程，通过牛顿法进行方程求解，对于n节点的天然气系统，当利用牛顿法进行第k次迭代求解时，其修正方程如下所示：

其中，

为所求函数的误差向量，为误差方程，J^(k)为此时雅可比矩阵，为此时的修正量向量，f_NG1…f_NGn表示对应节点1…节点n相关的天然气方程。通过反复迭代上述式子，所求变量逐渐趋近于系统真实解，直至满足收敛条件，输出结果。通过对初值进行优选，可用较少的迭代次数求得最终结果。

所述步骤(2)具体为：

令天然气系统方程用f(p,l)＝0表示，其中，p代表压力，l代表负荷。设天然气系统稳态运行点为(p₀,l₀)，受到扰动后系统的运行点将变为(p₀+Δp,l₀+Δl)。为了求出p与l变化量之间的关系，在(p₀,l₀)处将f(p,l)＝0按泰勒级数展开，取一次项，得：

其中，由于f(p₀,l₀)＝0，故有：

即：

令天然气节点压力-负荷灵敏度矩阵又由于负荷l是定量且通常已知，则即天然气压力-负荷灵敏度矩阵等于天然气系统潮流求解的雅可比矩阵求逆的负数。压力-负荷灵敏度的相关信息，一方面可为天然气系统注气点的位置优选提供帮助；另一方面，可为稳态综合求解中能源耦合环节的调整提供辅助信息。天然气系统的节点压力-负荷灵敏度分析可为负荷调整提供一定的理论依据。

步骤(3)具体包括：通过能源集线器模型，对区域综合能源系统中能源转换、分配与利用等耦合关系进行描述，将电力、天然气、热力等能源协同考虑；构建含空调系统、微型燃气轮机、燃气锅炉等元件的典型能源集线器模型；分析综合能源系统运行状态发生改变时，对能源耦合环节能量交互进行数值转换

为了对电力-天然气区域综合能源系统进行分析与求解，同时探讨天然气系统的变化对其自身以及与之耦合的能源系统的影响，本发明通过以下的实施例详细进行技术方案的详细描述：

参见图2，本发明所用三种典型能源集线器即Ⅰ、Ⅱ、Ⅲ型能源集线器，其中：

Ⅰ型能源集线器的主要元件包括变压器(Transformer，T)、空调系统(Air Conditioner，AC)以及燃气锅炉(Gas Furnace，GF)；L_e1与L_h1表示电力需求与热力需求，L_h1既可由GF供应，也可通过AC转化而来；P_e1与P_g1分别表示电力输入与天然气输入，λ₁表示分配系数，即λ₁P_e1表示电力输入分配给AC的功率；η^T、η^AC和η^GF分别表示T、AC和GF环节的能源转化效率。由此，该能源集线器可写成如下形式：

Ⅱ型能源集线器的主要元件包括换热器(Heat Exchanger，HE)、压缩机(Compressor，C)与电加热器(Heater，H)，电力系统通过H进行电热转换，并通过C向天然气系统提供能量，该部分所需功率与压缩机压缩比相关；L_e2与L_h2表示电力与热力需求，L_h2既可由C供应，也可通过H转化而来；P_e2与P_g2分别表示电力输入与天然气输入，λ₂表示分配系数，即λ₂P_e2表示电力输入分配给C的功率；η^HE、η^C和η^H分别表示HE、C和H环节的能源转化效率。该能源集线器可写成如下形式：

Ⅲ型能源集线器中，主要元件为微型燃气轮机(Micro Turbine，MT)与换热器(Heat Exchanger，HE)。天然气系统通过MT向电力系统供能，对其电压水平起支撑作用；同时，MT也是天然气系统的可变负荷，本文考虑其出力水平受天然气系统的影响。L_e3与L_h3表示电力需求与热力需求，L_h3由MT供应或转化；P_e3与P_g2分别表示电力输入与天然气输入，λ₃表示分配系数，即λ₃P_e3表示电力输入分配给MT的功率；与分别表示MT的气转电与气转热环节的效率。该能源集线器模型可表示为：

如图3所示的区域综合能源系统中，天然气系统为改进的低压配气网络。其中，节点1为气源点，节点12为注气点。该网络既体现了配气网络集中供气特性(节点1-8)，又体现出其辐射特性(节点9-11)，特殊用户1-3经过电驱动压缩机301分别与节点9-11相连。特殊用户有38mbar压力的天然气压力要求，故分别在相应支路增加压缩机，但压缩机变比有限制，其值取1.2-1.8，超过压缩机最大变比系统容易发生故障，且用户压力得不到满足。电力系统选取IEEE34节点三相不平衡系统。能源耦合环节选取上文所述的Ⅰ-Ⅲ型能源集线器。该系统耦合的复杂性具体体现在：

1)、天然气系统因含不同气质气体或加入注气点而对其自身产生影响。

2)、不同气质的天然气其热值不同，在不同情况下，能源集线器所需天然气功率与其对应的流量关系也随之变化。

3)、Ⅲ型能源集线器中的MT可对电力系统电压起支撑作用，但随着其出力的增加，天然气系统压力下降，为满足特殊用户压力需求，电驱动压缩机的变比增加，Ⅱ型能源集线器的电力输出随之增加，该部分功率由电力系统提供。

对天然气压力-负荷灵敏度进行分析，采用如图4所示的节点压力-负荷灵敏度矩阵S，矩阵元素s_x,y(x,y＝2,3,...11)表示节点x的负荷改变对节点y压力的影响(气源点是节点1)，每一行中加下划线标记的部分表示该行的最大值，即节点x负荷改变产生压力影响最大的节点。由该灵敏度矩阵可知，该矩阵数值较大元素出现在右下角框内，其最大值对应节点11，这是由于节点9-11处于线路末端且由单条管道供应，其负荷变化量对系统压力有最大的影响，与网络实际状况符合；压力-负荷灵敏度的相关信息，一方面可为天然气系统注气点的位置优选提供帮助；另一方面，可为稳态综合求解中能源耦合环节的调整提供辅助信息。

考虑天然气系统中引入注气点，结合当地可再生资源的有效利用，在原有网络节点附近增加分布式的注气点，并加入氢气、升级沼气等与不同气质的气体。选取在节点3附近增加注气点12，并加入相同流量(100m³/h)的氢气与升级沼气(来自P2G等可再生能源利用技术)。对于天然气系统，注气点的增加意味着网络结构以及天然气气质的同时改变；分别考虑：

1)、情况1：注气点注入氢气；

2)、情况2：注气点注入升级沼气；

在满足网络约束的条件下，探究此时MT在最大出力的情况下电力系统的节点电压的变化。

如图5所示，由该结果可知，在保持电力系统、天然气系统以及能源集线器能源需求整体不变的条件下，引入分布式注气点后天然气系统对电力系统的电压支撑作用提升明显。分布式注气点的加入对节点1-3影响较小，这是由于该部分节点与其气源点较近，其网络状态受到较小的改变。注气点注入不同气质的气体对天然气系统影响也不同，升级沼气的相对密度(值为0.58)较为接近原有网络的相对密度(值为0.6048)，总热值与原有网络也较为接近，且该情况下天然气系统对电力系统压力提升效果较好；相比较而言，此时注入的氢气相对密度(值为0.0696)与总热值(值为12.75)较原网络差别较大，虽然该情况下天然气系统压力降更小，但总热值的偏小意味着氢气需燃烧更多的量以满足相同的能量需求。此外，不同地区的天然气系统对氢气的容纳能力有较大区别，天然气系统存在的氢气量需控制在一定的范围之内。但总体来说，上述注气点的引入改善了天然气系统压力下降水平，提高了其对电力系统的电压支撑能力的上限，这对提高区域综合能源系统的稳定性具有一定的意义。

本领域技术人员可以理解附图只是一个优选实施例的示意图，上述本发明实施例序号仅仅为了描述，不代表实施例的优劣。

以上所述仅为本发明的较佳实施例，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。

参考文献：

[1]Li Q,An S,Gedra T W.Solving natural gas loadflow problems using electric loadflow techniques[C]//Proceedings of the North American Power Symposium,Rolla，USA，2003:1-7.

[2]Geidl M,Andersson G.A modeling and optimization approach for multiple energy carrier power flow[C]//In Proceedings of IEEE PES Power Tech,St.Petersburg,Russian Federation.2005:1-7.

[3]Abeysekera M,Wu J,Jenkins N,et al.Steady state analysis of gas networks with distributed injection of alternative gas[J].Applied Energy,2015,164:991–1002.

[4]Andrzej J.Osiadacz.Simulation and Analysis of Gas Network[M].London:E.&F.N.Spon Ltd,1986。