一种基于压缩传感的量子态重构方法及系统与流程

本申请涉及量子态重构
技术领域：
，更具体地说，涉及一种基于压缩传感的量子态重构方法及系统。
背景技术：
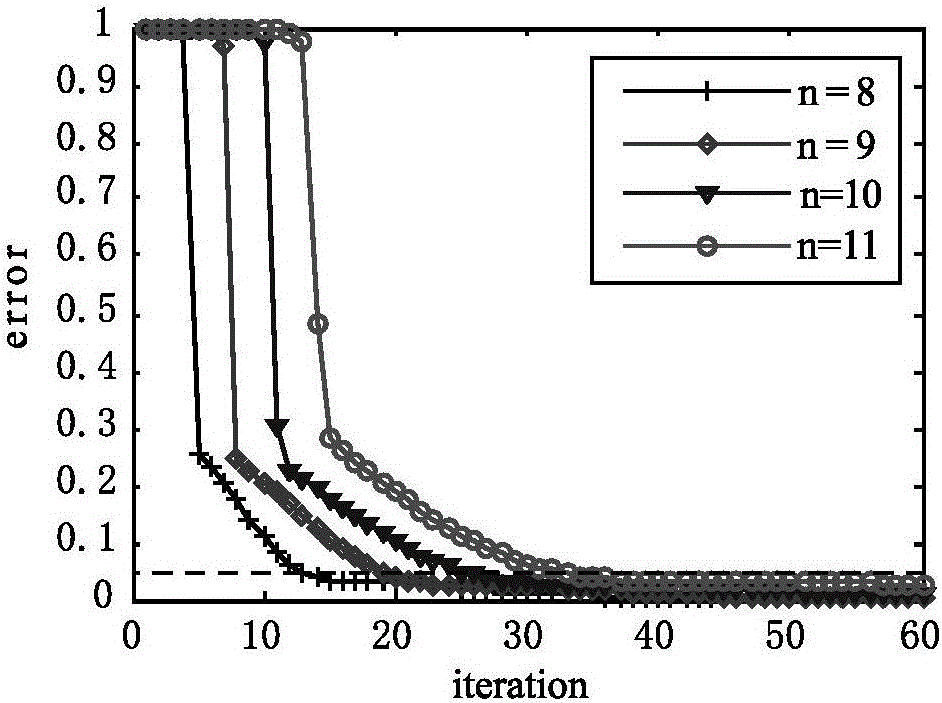
：一个具有n量子位(量子比特位)的量子系统的状态密度矩阵ρ是一个在希尔伯特空间里的d×d(其中d＝2n)矩阵，具有2n×2n＝4n个参数。因此，对该量子系统的进行量子态估计时所要估计的量子态参数数目的大小是随着n的增长呈指数增加的，换句话说，一个标准的量子态估计需要O(d2)次的测量配置。在实际应用中人们感兴趣的量子态往往是纯态或者近似纯态的，此时状态密度矩阵ρ是一个秩为r低秩的厄米矩阵。利用这一先验信息，人们将2006年由Candes、Donaho等人提出的压缩传感理论应用到量子态估计中，具体原理为：先通过一个测量矩阵A，将原始信号投影到低维空间；再通过求解一个优化问题，从少量的测量值中，精确重构出原始信号。压缩传感理论将对量子系统的量子态估计过程中的测量次数减少为M<<d2，一般定义测量率η＝M/d2。在基于压缩传感的量子态估计中，有两个重要问题需要解决：1、测量次数至少为多少时可以保证所选出的测量矩阵满足压缩传感所要求的低秩RIP条件，以至于能够在选中的少量测量数据中包含足够多的信息，重构出密度矩阵ρ；2、如何设计一个高效，并且鲁棒性强的重构算法，以便能够以压缩传感理论给出的最小测量率，达到高精度的优化问题的解。经过人们的不断努力，人们对于第一个问题已经得出结论：当测量次数M满足理论研究出的下界条件时，就可以使观测矩阵A以很高的概率满足低秩RIP理论。对于第二个问题，现有技术中公开了一种利用交替方向乘子法(AlternatingDirectionMethodofMultipliers，ADMM)求解基于压缩传感的量子态重构问题，获得了较快并且具备鲁棒性的量子态重构方法，但是由于在该方法中仍然存在大量的高阶矩阵求逆的运算导致花费时间很长，效率较低的问题。技术实现要素：为解决上述技术问题，本发明提供了一种基于压缩传感的量子态重构方法及系统，以实现降低量子态重构过程所需时间，提高运算效率的目的。为实现上述技术目的，本发明实施例提供了如下技术方案：一种基于压缩传感的量子态重构方法，包括：获取测量矩阵A和与其对应的测量值b，其中，M为测量次数，d＝2n，n为系统量子位数目，表示复数域，表示实数域；初始化密度矩阵ρ和拉格朗日乘子y，并设置迭代次数k＝1，其中，固定所述密度矩阵ρ＝ρk和所述拉格朗日乘子y＝yk，利用第一预设公式更新辅助变量，所述第一预设公式为ek+1＝(γ/λ+γλ)(-yk/λ-(Avec(ρk)-b))，其中，vec(X)表示按列将矩阵X展开为一个列向量，γ>0，表示权重值，λ>0，表示惩罚参数值；固定所述辅助变量e＝ek+1和所述拉格朗日乘子y＝yk，利用第二预设公式更新所述密度矩阵ρ＝ρk+1，所述第二预设公式为其中，为奇异值收缩算子：USVT为矩阵X的奇异值分解；为软阈值算子：表示将向量X按列排成矩阵，t>0为梯度下降步长；固定所述辅助变量e＝ek+1和所述密度矩阵ρ＝ρk+1，利用第三预设公式更新所述拉格朗日乘子，所述第三预设公式为yk+1＝yk+κλ(Avec(ρk+1)+ek+1-b)，其中，κ为常数，且κ>0；判断所述辅助变量ek+1是否满足停止条件，如果是，则将获得的密度矩阵ρk+1作为计算密度矩阵并计算归一化密度矩阵估计误差，输出计算密度矩阵和矩阵估计误差；如果否，则更新迭代次数k＝k+1，返回固定所述密度矩阵ρ＝ρk和所述拉格朗日乘子y＝yk，利用第一预设公式更新辅助变量e的步骤。可选的，所述初始化密度矩阵ρ和拉格朗日乘子y包括：定义待求解方程：其增广拉格朗日方程为其中，vec(X)表示按列将矩阵X展开为一个列向量，为ρ的共轭转置，||||*表示核范数，||||2表示2-范数运算；求解所述带求解方程获得初始化的密度矩阵ρ和拉格朗日乘子y。可选的，所述计算归一化密度矩阵估计误差包括：利用第四预设公式计算所述归一化密度矩阵估计误差，所述第四预设公式为其中，error表示所述归一化密度矩阵估计误差，为计算密度矩阵，ρ为初始化的密度矩阵，||||F表示范数运算。可选的，所述停止条件为||b-A·vec(ρk)-ek||F/||b||F＜ε1或k>kmax，其中，ε1为容限函数，kmax为最大迭代次数。一种基于压缩传感的量子态重构系统，包括：矩阵获取模块，用于获取测量矩阵A和与其对应的测量值b，其中，M为测量次数，d＝2n，n为系统量子位数目，表示复数域，表示实数域；初始化模块，用于初始化密度矩阵ρ和拉格朗日乘子y，并设置迭代次数k＝1，其中，第一迭代模块，用于固定所述密度矩阵ρ＝ρk和所述拉格朗日乘子y＝yk，利用第一预设公式更新辅助变量，所述第一预设公式为ek+1＝(γ/λ+γλ)(-yk/λ-(Avec(ρk)-b))，其中，vec(X)表示按列将矩阵X展开为一个列向量，γ>0，表示权重值，λ>0，表示惩罚参数值；第二迭代模块，用于固定所述辅助变量e＝ek+1和所述拉格朗日乘子y＝yk，利用第二预设公式更新所述密度矩阵ρ＝ρk+1，所述第二预设公式为其中，为奇异值收缩算子：USVT为矩阵X的奇异值分解；为软阈值算子：表示将向量X按列排成矩阵，t>0为梯度下降步长；第三迭代模块，用于固定所述辅助变量e＝ek+1和所述密度矩阵ρ＝ρk+1，利用第三预设公式更新所述拉格朗日乘子，所述第三预设公式为yk+1＝yk+κλ(Avec(ρk+1)+ek+1-b)，其中，κ为常数，且κ>0；判断模块，用于判断所述辅助变量ek+1是否满足停止条件，如果是，则将获得的密度矩阵ρk+1作为计算密度矩阵并计算归一化密度矩阵估计误差，输出计算密度矩阵和矩阵估计误差；如果否，则更新迭代次数k＝k+1，返回所述第一迭代模块。可选的，所述初始化模块初始化密度矩阵ρ和拉格朗日乘子y具体用于定义待求解方程：其增广拉格朗日方程为其中，vec(X)表示按列将矩阵X展开为一个列向量，为ρ的共轭转置，||||2表示2-范数运算；求解所述带求解方程获得初始化的密度矩阵ρ和拉格朗日乘子y。可选的，所述判断模块计算归一化密度矩阵估计误差具体用于利用第四预设公式计算所述归一化密度矩阵估计误差，所述第四预设公式为其中，error表示所述归一化密度矩阵估计误差，为计算密度矩阵，ρ为初始化的密度矩阵，||·||F表示范数运算。可选的，所述停止条件为||b-A·vec(ρk)-ek||F/||b||F＜ε1或k>kmax，其中，ε1为容限函数，kmax为最大迭代次数。从上述技术方案可以看出，本发明实施例提供了一种基于压缩传感的量子态重构方法及系统，其中，所述基于压缩传感的量子态重构方法将交替方向乘子法(AlternatingDirectionMethodofMultipliers，ADMM)和迭代阈值收缩法(IterativeShrinkage-ThresholdingAlgorithm，ISTA)相结合，在迭代过程中引入辅助变量e，使得在ADMM算法框架下求解量子态重构问题，可以更快地得到更精确的解；并且在更新所述密度矩阵的过程中通过3次加入括号的方式改变了常规的计算顺序，这一运算方式使得计算复杂度大大降低：首先利用第一对括号，优先计算v1＝(A·vec(ρk)+ek+1-b+yk/λ)，得到M×1的向量v1；其次，利用第二对括号，使与向量v1相乘得到d2×1的向量v2＝A*·v1，这两步运算过程可以有效避免高维矩阵和的直接相乘，使得计算复杂度由O(Md4)下降为O(Md2)。最后，对于梯度下降步长t>0的乘法，通过加入第三对括号，使得运算顺序从t·A*·v1变成了t·(A*·v1)，所参与的乘法次数从d2×M次下降到了d2次，对于高量子位量子系统，这样的下降幅度是巨大的。例如，当量子位n＝12时，d2＝224＝1.6777216e7，乘法次数下降到原来的千万分之一。综上，所述基于压缩传感的量子态重构方法能够大大降低了运算次数，进而降低了量子态重构过程所需时间，提高了运算效率。进一步的，所述基于压缩传感的量子态重构方法直接构造M×d2的测量矩阵A，采用更为普遍的、考虑测量值中含有高斯白噪声的凸优化模型，将ADMM算法中拉格朗日乘子更新的固定步长，变为可调步长，加快算法的收敛速度，减小迭代次数和计算时间。附图说明为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图获得其他的附图。图1为本申请的一个实施例提供的一种基于压缩传感的量子态重构方法的流程示意图；图2为量子位分别为8、9、10和11时，利用基于压缩传感的量子态重构方法的实际效果示意图；图3为假设测量值包含信噪比为70分贝的高斯分布的白噪声，量子位为11，固定测量比率为0.6％，最大迭代次数为60次时，利用基于压缩传感的量子态重构方法获得的归一化密度矩阵估计误差随迭代次数变化的曲线示意图；图4为本申请的一个实施例提供的一种基于压缩传感的量子态重构系统的结构示意图。具体实施方式下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。本申请实施例提供了一种基于压缩传感的量子态重构方法，如图1所示，包括：S101：获取测量矩阵A和与其对应的测量值b，其中，M为测量次数，d＝2n，n为系统量子位数目，表示复数域，表示实数域；S102：初始化密度矩阵ρ和拉格朗日乘子y，并设置迭代次数k＝1，其中，S103：固定所述密度矩阵ρ＝ρk和所述拉格朗日乘子y＝yk，利用第一预设公式更新辅助变量，所述第一预设公式为ek+1＝(γ/λ+γλ)(-yk/λ-(Avec(ρk)-b))，其中，vec(X)表示按列将矩阵X展开为一个列向量，γ>0，表示权重值，λ>0，表示惩罚参数值；S104：固定所述辅助变量e＝ek+1和所述拉格朗日乘子y＝yk，利用第二预设公式更新所述密度矩阵ρ＝ρk+1，所述第二预设公式为其中，为奇异值收缩算子：USVT为矩阵X的奇异值分解；为软阈值算子：表示将向量X按列排成矩阵，t>0为梯度下降步长；S105：固定所述辅助变量e＝ek+1和所述密度矩阵ρ＝ρk+1，利用第三预设公式更新所述拉格朗日乘子，所述第三预设公式为yk+1＝yk+κλ(Avec(ρk+1)+ek+1-b)，其中，κ为常数，且κ>0；S106：判断所述辅助变量ek+1是否满足停止条件，如果是，则将获得的密度矩阵ρk+1作为计算密度矩阵并计算归一化密度矩阵估计误差，输出计算密度矩阵和矩阵估计误差；如果否，则更新迭代次数k＝k+1，返回固定所述密度矩阵ρ＝ρk和所述拉格朗日乘子y＝yk，利用第一预设公式更新辅助变量e的步骤。所述基于压缩传感的量子态重构方法将交替方向乘子法(AlternatingDirectionMethodofMultipliers，ADMM)和迭代阈值收缩法(IterativeShrinkage-ThresholdingAlgorithm，ISTA)相结合，在迭代过程中引入辅助变量e，使得在ADMM算法框架下求解量子态重构问题，可以更快地得到更精确的解；并且在更新所述密度矩阵的过程中通过3次加入括号的方式改变了常规的计算顺序，这一运算方式使得计算复杂度大大降低：首先利用第一对括号，优先计算v1＝(A·vec(ρk)+ek+1-b+yk/λ)，得到M×1的向量v1；其次，利用第二对括号，使与向量v1相乘得到d2×1的向量v2＝A*·v1，这两步运算过程可以有效避免高维矩阵和的直接相乘，使得计算复杂度由O(Md4)下降为O(Md2)。最后，对于梯度下降步长t>0的乘法，通过加入第三对括号，使得运算顺序从t·A*·v1变成了t·(A*·v1)，所参与的乘法次数从d2×M次下降到了d2次，对于高量子位量子系统，这样的下降幅度是巨大的。例如，当量子位n＝12时，d2＝224＝1.6777216e7，乘法次数下降到原来的千万分之一。综上，所述基于压缩传感的量子态重构方法能够大大降低了运算次数，进而降低了量子态重构过程所需时间，提高了运算效率。进一步的，所述基于压缩传感的量子态重构方法直接构造M×d2的测量矩阵A，采用更为普遍的、考虑测量值中含有高斯白噪声的凸优化模型，将ADMM算法中拉格朗日乘子更新的固定步长，变为可调步长，加快算法的收敛速度，减小迭代次数和计算时间。在上述实施例的基础上，在本申请的一个实施例中，所述初始化密度矩阵ρ和拉格朗日乘子y包括：定义待求解方程：其增广拉格朗日方程为其中，vec(X)表示按列将矩阵X展开为一个列向量，为ρ的共轭转置，||||*表示核范数，||||2表示2-范数运算；求解所述带求解方程获得初始化的密度矩阵ρ和拉格朗日乘子y。需要说明的是，s.t.(subjectto)表示受约束。在上述实施例的基础上，在本申请的另一个实施例中，所述计算归一化密度矩阵估计误差包括：利用第四预设公式计算所述归一化密度矩阵估计误差，所述第四预设公式为其中，error表示所述归一化密度矩阵估计误差，为计算密度矩阵，ρ为初始化的密度矩阵，||||F表示范数运算。在上述实施例的基础上，在本申请的一个实施例中，所述停止条件为||b-A·vec(ρk)-ek||F/||b||F＜ε1或k>kmax，其中，ε1为容限函数，kmax为最大迭代次数。在上述实施例的基础上，本申请的一个具体实施例对所述基于压缩传感的量子态重构方法的实际效果进行了验证，参考图2和表1，图2和表1为无噪声情况下不同量子位归一化密度矩阵估计误差error以及所达到的具体性能；当量子位n分别为8、9、10和11，测量比率分别固定为η＝3％、1.7％、1％和0.6％时，在不同量子位情况下所得到的归一化密度矩阵估计误差随迭代次数变化结果如图2所示，其中，横坐标为迭代次数，纵坐标为归一化密度矩阵估计误差，标记有加号、菱形、三角和圆圈的曲线分别为n＝8、9、10和11时，归一化密度矩阵估计误差随迭代次数的变化曲线，虚线代表归一化密度矩阵估计误差为5％。所述基于压缩传感的量子态重构方法的具体性能指标如表1所示。实验所采用的计算机为：IntelXeonE5-2407CPU、2核、主频2.4GHz、内存16G。表1基于压缩传感的量子态重构方法的具体性能指标量子位nn＝8n＝9n＝10n＝11测量比率η3％1.7％1％0.6％error4.59％4.89％4.96％4.54％迭代次数(次)13192533重构时间(秒)3.4211.6131.7099.26图3为假设测量值b中包含信噪比为70分贝的高斯分布的白噪声，量子位n＝11，固定测量比率η＝0.6％，最大迭代次数为60次时，所得到的归一化密度矩阵估计误差随迭代次数变化的实验结果，其中虚线代表归一化密度矩阵估计误差为5％。相应的，本申请实施例还提供了一种基于压缩传感的量子态重构系统，如图4所示，包括：矩阵获取模块100，用于获取测量矩阵A和与其对应的测量值b，其中，M为测量次数，d＝2n，n为系统量子位数目，表示复数域，表示实数域；初始化模块200，用于初始化密度矩阵ρ和拉格朗日乘子y，并设置迭代次数k＝1，其中，第一迭代模块300，用于固定所述密度矩阵ρ＝ρk和所述拉格朗日乘子y＝yk，利用第一预设公式更新辅助变量，所述第一预设公式为ek+1＝(γ/λ+γλ)(-yk/λ-(Avec(ρk)-b))，其中，vec(X)表示按列将矩阵X展开为一个列向量，γ>0，表示权重值，λ>0，表示惩罚参数值；第二迭代模块400，用于固定所述辅助变量e＝ek+1和所述拉格朗日乘子y＝yk，利用第二预设公式更新所述密度矩阵ρ＝ρk+1，所述第二预设公式为其中，为奇异值收缩算子：USVT为矩阵X的奇异值分解；为软阈值算子：表示将向量X按列排成矩阵，t>0为梯度下降步长；第三迭代模块500，用于固定所述辅助变量e＝ek+1和所述密度矩阵ρ＝ρk+1，利用第三预设公式更新所述拉格朗日乘子，所述第三预设公式为yk+1＝yk+κλ(Avec(ρk+1)+ek+1-b)，其中，κ为常数，且κ>0；判断模块600，用于判断所述辅助变量ek+1是否满足停止条件，如果是，则将获得的密度矩阵ρk+1作为计算密度矩阵并计算归一化密度矩阵估计误差，输出计算密度矩阵和矩阵估计误差；如果否，则更新迭代次数k＝k+1，返回所述第一迭代模块。所述基于压缩传感的量子态重构系统将交替方向乘子法(AlternatingDirectionMethodofMultipliers，ADMM)和迭代阈值收缩法(IterativeShrinkage-ThresholdingAlgorithm，ISTA)相结合，在迭代过程中引入辅助变量e，使得在ADMM算法框架下求解量子态重构问题，可以更快地得到更精确的解；并且在更新所述密度矩阵的过程中通过3次加入括号的方式改变了常规的计算顺序，这一运算方式使得计算复杂度大大降低：首先利用第一对括号，优先计算v1＝(A·vec(ρk)+ek+1-b+yk/λ)，得到M×1的向量v1；其次，利用第二对括号，使与向量v1相乘得到d2×1的向量v2＝A*·v1，这两步运算过程可以有效避免高维矩阵和的直接相乘，使得计算复杂度由O(Md4)下降为O(Md2)。最后，对于梯度下降步长t>0的乘法，通过加入第三对括号，使得运算顺序从t·A*·v1变成了t·(A*·v1)，所参与的乘法次数从d2×M次下降到了d2次，对于高量子位量子系统，这样的下降幅度是巨大的。例如，当量子位n＝12时，d2＝224＝1.6777216e7，乘法次数下降到原来的千万分之一。综上，所述基于压缩传感的量子态重构方法能够大大降低了运算次数，进而降低了量子态重构过程所需时间，提高了运算效率。进一步的，所述基于压缩传感的量子态重构系统直接构造M×d2的测量矩阵A，采用更为普遍的、考虑测量值中含有高斯白噪声的凸优化模型，将ADMM算法中拉格朗日乘子更新的固定步长，变为可调步长，加快算法的收敛速度，减小迭代次数和计算时间。在上述实施例的基础上，在本申请的一个实施例中，所述初始化模块200初始化密度矩阵ρ和拉格朗日乘子y具体用于定义待求解方程：其增广拉格朗日方程为其中，vec(X)表示按列将矩阵X展开为一个列向量，为ρ的共轭转置，||||*表示核范数，||||2表示2-范数运算；求解所述带求解方程获得初始化的密度矩阵ρ和拉格朗日乘子y。需要说明的是，s.t.(subjectto)表示受约束。在上述实施例的基础上，在本申请的另一个实施例中，所述判断模块600计算归一化密度矩阵估计误差具体用于利用第四预设公式计算所述归一化密度矩阵估计误差，所述第四预设公式为其中，error表示所述归一化密度矩阵估计误差，为计算密度矩阵，ρ为初始化的密度矩阵，||||F表示范数运算。在上述实施例的基础上，在本申请的一个实施例中，所述停止条件为||b-A·vec(ρk)-ek||F/||b||F＜ε1或k>kmax，其中，ε1为容限函数，kmax为最大迭代次数。在上述实施例的基础上，本申请的一个具体实施例对所述基于压缩传感的量子态重构系统的实际效果进行了验证，参考图2和表1，图2和表1为无噪声情况下不同量子位归一化密度矩阵估计误差error以及所达到的具体性能；当量子位n分别为8、9、10和11，测量比率分别固定为η＝3％、1.7％、1％和0.6％时，在不同量子位情况下所得到的归一化密度矩阵估计误差随迭代次数变化结果如图2所示，其中，横坐标为迭代次数，纵坐标为归一化密度矩阵估计误差，标记有加号、菱形、三角和圆圈的曲线分别为n＝8、9、10和11时，归一化密度矩阵估计误差随迭代次数的变化曲线，虚线代表归一化密度矩阵估计误差为5％。所述基于压缩传感的量子态重构系统的具体性能指标如表1所示。实验所采用的计算机为：IntelXeonE5-2407CPU、2核、主频2.4GHz、内存16G。表1基于压缩传感的量子态重构系统的具体性能指标量子位nn＝8n＝9n＝10n＝11测量比率η3％1.7％1％0.6％error4.59％4.89％4.96％4.54％迭代次数(次)13192533重构时间(秒)3.4211.6131.7099.26图3为假设测量值b中包含信噪比为70分贝的高斯分布的白噪声，量子位n＝11，固定测量比率η＝0.6％，最大迭代次数为60次时，所得到的归一化密度矩阵估计误差随迭代次数变化的实验结果，其中虚线代表归一化密度矩阵估计误差为5％。综上所述，本申请实施例提供了一种基于压缩传感的量子态重构方法及系统，其中，所述基于压缩传感的量子态重构方法将交替方向乘子法(AlternatingDirectionMethodofMultipliers，ADMM)和迭代阈值收缩法(IterativeShrinkage-ThresholdingAlgorithm，ISTA)相结合，在迭代过程中引入辅助变量e，使得在ADMM算法框架下求解量子态重构问题，可以更快地得到更精确的解；并且在更新所述密度矩阵的过程中通过3次加入括号的方式改变了常规的计算顺序，这一运算方式使得计算复杂度大大降低：首先利用第一对括号，优先计算v1＝(A·vec(ρk)+ek+1-b+yk/λ)，得到M×1的向量v1；其次，利用第二对括号，使与向量v1相乘得到d2×1的向量v2＝A*·v1，这两步运算过程可以有效避免高维矩阵和的直接相乘，使得计算复杂度由O(Md4)下降为O(Md2)。最后，对于梯度下降步长t>0的乘法，通过加入第三对括号，使得运算顺序从t·A*·v1变成了t·(A*·v1)，所参与的乘法次数从d2×M次下降到了d2次，对于高量子位量子系统，这样的下降幅度是巨大的。例如，当量子位n＝12时，d2＝224＝1.6777216e7，乘法次数下降到原来的千万分之一。综上，所述基于压缩传感的量子态重构方法能够大大降低了运算次数，进而降低了量子态重构过程所需时间，提高了运算效率。进一步的，所述基于压缩传感的量子态重构方法直接构造M×d2的测量矩阵A，采用更为普遍的、考虑测量值中含有高斯白噪声的凸优化模型，将ADMM算法中拉格朗日乘子更新的固定步长，变为可调步长，加快算法的收敛速度，减小迭代次数和计算时间。本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的这些实施例，而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。当前第1页1 2 3