一种基于随机矩阵理论的混沌时间序列的识别方法与流程

本发明涉及一种混沌时间序列的识别方法，具体是一种基于随机矩阵理论的混沌时间序列的识别方法。

背景技术：

混沌时间序列普遍存在于物理、通信、生物、气象和经济等领域中。由于混沌动力系统产生的时间序列与随机过程产生的噪声时间序列存在着相似的时域无规律行为和频谱特性等，使得它们很难被区分。如何对混沌时间序列和噪声时间序列进行有效地辨识，不仅具有理论意义，而且具有很好的工程实用价值。

识别混沌时间序列的一般方法分为定性和定量两种方式。定性方法主要通过比较混沌信号与噪声的时频域特性来确认系统是否为混沌的。很明显，这种方法主要的缺点就是缺乏客观定量的描述，主观性较强。而定量方法是通过计算混沌系统的某些特征量，根据特征量数值大小来判别混沌是否存在。这些混沌特征量包括李雅普诺夫指数(lyapunovexponent)、柯尔莫哥洛夫熵(kolmogoroventropy)、分数维(fractaldimension)等。由于计算以上特征量数值的算法要求时间序列的长度较长，且易受噪声的干扰，所以在一些短的或含有噪声的混沌时间序列中，这些方法的应用就会受到限制，从而无法准确的对混沌时间序列进行识别。

技术实现要素：

针对上述现有技术存在的问题，本发明提供一种基于随机矩阵理论的混沌时间序列的识别方法，其可对序列较短的或含有噪声的混沌时间序列进行识别，从而便于后续的研究，其具有处理过程简单，且其普适性和鲁棒性均较好。

为了实现上述目的，本发明采用的技术方案是：一种基于随机矩阵理论的混沌时间序列的识别方法，其具体步骤为：

a、随机选取预识别的时间序列，所述时间序列的选取范围为噪声时间序列和已知混沌系统的时间序列中的一种，并根据该时间序列构建原始矩阵x；

b、对矩阵x进行归一化处理，将其转化为行向量均值为0，方差为1的非厄米特矩阵

c、将得到的非厄米特矩阵计算出其奇异值等价矩阵xu，然后对该奇异值等价矩阵xu计算得到标准的矩阵积

d、根据标准的矩阵积计算得出其特征值，并计算出特征值的平均谱半径；

e、根据随机矩阵理论的单环定律，识别出该时间序列为噪声时间序列或混沌时间序列。

进一步，所述步骤a中的已知混沌系统共三个，分别为lorenz系统、系统和hénon映射，其中lorenz系统和系统是三维连续系统，hénon映射是二维离散系统，具体为：

lorenz系统模型

当参数值取σ＝10，β＝8/3和ρ＝28时，该系统处于混沌状态；

系统模型

当参数取a＝0.2，b＝0.2，c＝5.7时，系统处于混沌状态；

hénon映射是二维离散时间动态系统，在平面上取一个点(xn,yn)，并将其映射到一个新的点：

当参数取a＝1.4，b＝0.3，初始条件为(x0,y0)＝(0,0)时，hénon映射处于混沌状态。

进一步，所述预识别的时间序列表示为v＝(v1,...vi,...vi+mn,...vt)，采用v的部分或全部元素构造一个m×n的原始矩阵x。

进一步，所述步骤b中，对矩阵x归一化，得到非厄米特矩阵

其中

进一步，步骤(3)的具体过程为：

计算所述非厄米特矩阵的奇异值等价矩阵xu；

根据所述奇异值等价矩阵xu计算矩阵乘积

根据上述矩阵乘积求取标准的矩阵积其每行元素满足

进一步，所述步骤(4)中的平均谱半径为线性特征值统计量的一种，定义为矩阵的所有特征值在复平面上距离原点的平均值：

其中是矩阵的第i个特征值。

进一步，在步骤(5)中，根据随机矩阵理论中的单环定律：

当m,n→∞，且满足c＝m/n∈(0,1]时，若的特征值分布在复平面上一个外环半径为1，内环半径为(1-c)^l2的圆环之间，且其特征值的平均谱半径位于圆环内，则确定该时间序列为噪声时间序列；若的特征值分布在圆环的内环内，且其特征值的平均谱半径分布在内环内，则确定该时间序列为混沌时间序列。

与现有技术相比，本发明优点如下：

(1)本发明使用的随机矩阵理论方法是一种普适性的统计分析方法，无需建立对象详细的数学模型，在对混沌时间序列的识别上简单易行；

(2)本发明同时也是一种简易的数据驱动的辨识方法。在辨识噪声或混沌时间序列时只需获取相应的原始数据即可进行，无需对原始数据进行额外的假设或者进行系统的机理分析等。

(3)本发明可对序列较短的或含有噪声的混沌时间序列进行识别，从而便于后续的研究，其具有处理过程简单，且其普适性和鲁棒性均较好。

(4)本发明利用线性特征值统计量—平均谱半径，可以对混沌时间序列定量的描述。

附图说明

图1是本发明的识别流程图；

图2a是本发明实施例中噪声时间序列的单环特征谱分布及平均谱半径分布图；

图2b是本发明实施例中lorenz系统的时间序列的单环特征谱分布及平均谱半径分布图；

图2c是本发明实施例中系统的时间序列的单环特征谱分布及平均谱半径分布图；

图2d是本发明实施例中hénon映射的时间序列的单环特征谱分布及平均谱半径分布图；

图3是本发明实施例中噪声和三种不同混沌时间序列的平均谱半径数据图；

图4a是本发明实施例中lorenz系统短混沌时间序列的单环特征谱分布及平均谱半径分布图；

图4b是本发明实施例中系统短混沌时间序列的单环特征谱分布及平均谱半径分布图；

图4c是本发明实施例中hénon映射短混沌时间序列的单环特征谱分布及平均谱半径分布图；

图5是本发明实施例中噪声和三种不同短混沌时间序列的平均谱半径数据图；

图6a是本发明实施例中lorenz系统不同信噪比混沌时间序列的单环特征谱分布及平均谱半径分布图；

图6b是本发明实施例中系统不同信噪比混沌时间序列的单环特征谱分布及平均谱半径分布图；

图6c是本发明实施例中hénon映射不同信噪比混沌时间序列的单环特征谱分布及平均谱半径分布图；

图7是本发明实施例中噪声和三种不同混沌时间序列在不同信噪比的平均谱半径数据图；

图8a是本发明仿真实验中原油价格数据的单环特征谱分布及平均谱半径分布图；

图8b是本发明仿真实验中肌电信号数据的单环特征谱分布及平均谱半径分布图。

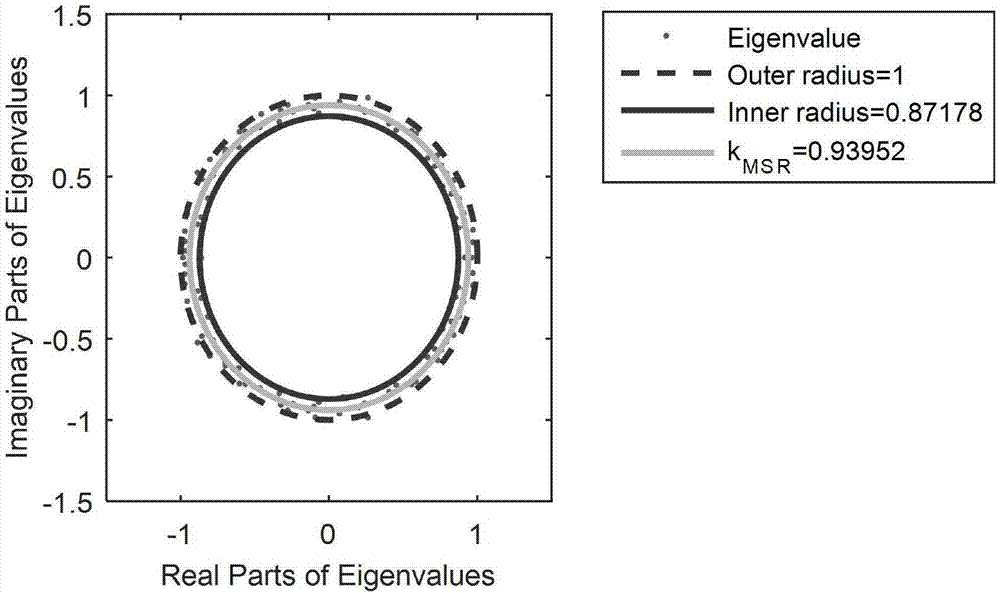
图中：eigenvalue表示特征值；outerradius表示外环；innerradius表示内环。

具体实施方式

下面将对本发明作进一步说明。

如图1所示，本发明的具体步骤为：

a、随机选取预识别的时间序列，所述时间序列的选取范围为噪声时间序列和已知混沌系统的时间序列中的一种，并根据该时间序列构建原始矩阵x；当获取的数据量充足时，将这些数据看作是一个时间序列v＝(v1,...vi,...vi+mn,...vt)，可以使用v的部分或全部元素构造一个m×n的原始矩阵x；

如仿真实验中，时间序列v来源于不同混沌系统中变量y产生的数据点，矩阵x的大小为120×500，因此c＝m/n＝0.24；

由于在实际使用过程中可能获取的数据量会比较少。少量数据的情形中，获取的数据只能构成一个短的时间序列v＝(v1,...vi,...vi+m+n,...vt)。为了能构造出维数较大的矩阵x，在此允许相邻两列之间的元素最大限度的重叠：

与长时间序列的实验相比，构造该矩阵x所需的数据点数较少，但是矩阵的维数较大，因而能够产生足够多的特征值用于统计分析。

b、对矩阵x进行归一化处理，将其转化为行向量均值为0，方差为1的非厄米特矩阵按公式(9)对原始矩阵x归一化处理，得到非厄米特矩阵

其中xi＝(xi1,xi2,...,xin)，是样本xi的平均值，σ(xi)是样本的标准差。

c、将得到的非厄米特矩阵计算出其奇异值等价矩阵xu，然后对该奇异值等价矩阵xu计算得到标准的矩阵积

首先计算出非厄米特矩阵的奇异值等价矩阵xu∈^m×n，

式中u是haar酉矩阵，表示的复共轭转置，此时，满足

随后计算矩阵积

其中是对l个这样的非厄米特矩阵经过变换之后，得到的l个对应的奇异值等价矩阵。

最后，矩阵积按照公式(12)逐行进行归一化，求取标准的矩阵积其每行元素满足

d、根据标准的矩阵积计算得出其特征值，并计算出特征值的平均谱半径；

由于矩阵的单个特征值具有随机性无法反映矩阵元素的统计特性，而矩阵迹可反映矩阵元素的这种特性，故引入能够描述矩阵迹的线性特征值统计量作为评价指标，来分析特征值的分布。平均谱半径作为线性特征值统计量的一种，其定义为复平面上矩阵的所有特征值距离中心点的平均值:

这里是矩阵的第i个特征值。

e、根据随机矩阵理论的单环定律，识别出该时间序列为噪声时间序列或混沌时间序列。

根据随机矩阵理论中的单环定律：

当m,n→∞，且满足c＝m/n∈(0,1]时，若的特征值分布在复平面上一个外环半径为1，内环半径为(1-c)^l/2的圆环之间，且其特征值的平均谱半径位于圆环内，则确定该时间序列为噪声时间序列；若的特征值分布在圆环的内环内，且其特征值的平均谱半径分布在内环内，则确定该时间序列为混沌时间序列。其中平均谱半径kmsr表征了时间序列的随机程度:若kmsr在圆环的内环和圆环的外环之间，则说明该时间序列是噪声；反之，则说明数据点之间存在较强的相关性。由于混沌时间序列具有内在的相关性，因此其平均谱半径kmsr小于圆环的内环。

仿真验证：

步骤1

当获取的数据充足时，三个混沌系统和噪声的特征值经验分布谱如图2a、2b、2c、2d所示。图3是使用不同的数据点，进行20次仿真实验得到特征值的平均谱半径值。

由图2a、2b、2c、2d和图3可见，随机噪声的特征值绝大多数分布在圆环内(即外环与内环之间)，也有极少数特征值分布在圆环之外，少数的“离群值”不影响单环定律的应用。而lorenz系统、系统和hénon映射的特征值基本上分布在内圆中，其平均谱半径也都小于圆环内径，说明这些时间序列的随机性比噪声要弱，不再符合单环定律。这种差异表明隐藏在时间序列中的相关性使得混沌系统特征值分布不同于随机噪声特征值分布。其中离散时间动态系统hénon映射的特征值分布更接近随机噪声的特征值分布，其特征值的平均谱半径比lorenz系统和系统的也更接近圆环内径，这说明了离散混沌时间序列相对连续混沌时间序列表现出更多的随机性。

步骤2

当获取的数据点非常少时，可以得到三个混沌系统它们的特征值分布(如图4a、4b、4c)以及20次仿真的特征值的平均谱半径(如图5)。

由如图4a、4b、4c可见，lorenz系统、系统和hénon映射的特征值分布和图2a、2b、2c、2d所得到的特征值分布基本一致，图5显示的特征值的平均谱半径值也基本不变。虽然可利用的混沌时间序列的数据点非常少，但本发明的方法仍能够很好地识别混沌时间序列，证明该方法可以有效地识别出短时间序列的混沌特性。

步骤3

当测量数据夹杂着观测噪声时，这将对区分的准确性产生一定的影响。在仿真实验中把观测噪声加到混沌时间序列v＝(v1,...vi,...vt)中，来验证方法的鲁棒性。假设观测噪声服从正态分布，均值为0，方差为因为观测噪声的大小决定着区分的准确性和有效性，所以引入信噪比(snr)来表示混沌时间序列中包含观测噪声的相对强度：

其中和分别表示信号(混沌时间序列)和观测噪声的方差。图6a、6b和6c显示了不同信噪比下特征值的分布情况。由图6a、6b和6c可见，随着观测噪声的增加，三个混沌系统的特征值分布逐渐接近圆环。图7给出了信噪比从1到10变化时混沌时间序列特征值的平均谱半径。可以看出当信噪比比较小时，平均谱半径依然小于圆环内径，仍能够可以有效地区分噪声信号和混沌时间序列；但是随着观测噪声强度的增大，区分噪声和混沌时间序列变得越来越困难。

步骤4

为了进一步验证方法的有效性，利用从美联储(https://fred.stlouisfed.org/)和uci(https://archive.ics.uci.edu/ml/)获得的原油价格数据的时间序列和肌电信号数据的时间序列来识别混沌特性。原油作为一种基础的能源产品，其价格的变动影响着经济领域的方方面面，原油价格的相关问题已经得到越来越多的关注和深入研究；肌电图数据通过测量肌肉的电活动，以收集关于肌肉和神经系统的信息，常被用于诊断肌肉无力或麻痹、神经损伤等，也被用于运动学、步态研究和假体设计等领域。目前已经证实原油价格数据和肌电信号数据均为混沌时间序列。

由于数据量相对较少，通过从获得的数据中取619个连续数据点进行分析。实验结果如图8a和8b所示，特征值基本上分布在圆环内径之内，表明无论是原油价格波动时间序列，还是肌电图数据，都不是完全随机的时间序列，数据之间存在着相关性，符合混沌时间序列的特征值分布，能够很好的反映出其混沌的特性，能够与随机噪声进行区分，从而进一步证明了本发明可实现识别噪声时间序列和混沌时间序列的有效性。