基于真三维显示系统的Roesser模型及其实现方法与流程

本发明涉及一种基于真三维显示系统的roesser模型及其实现方法，属于多维系统控制理论技术领域。

背景技术

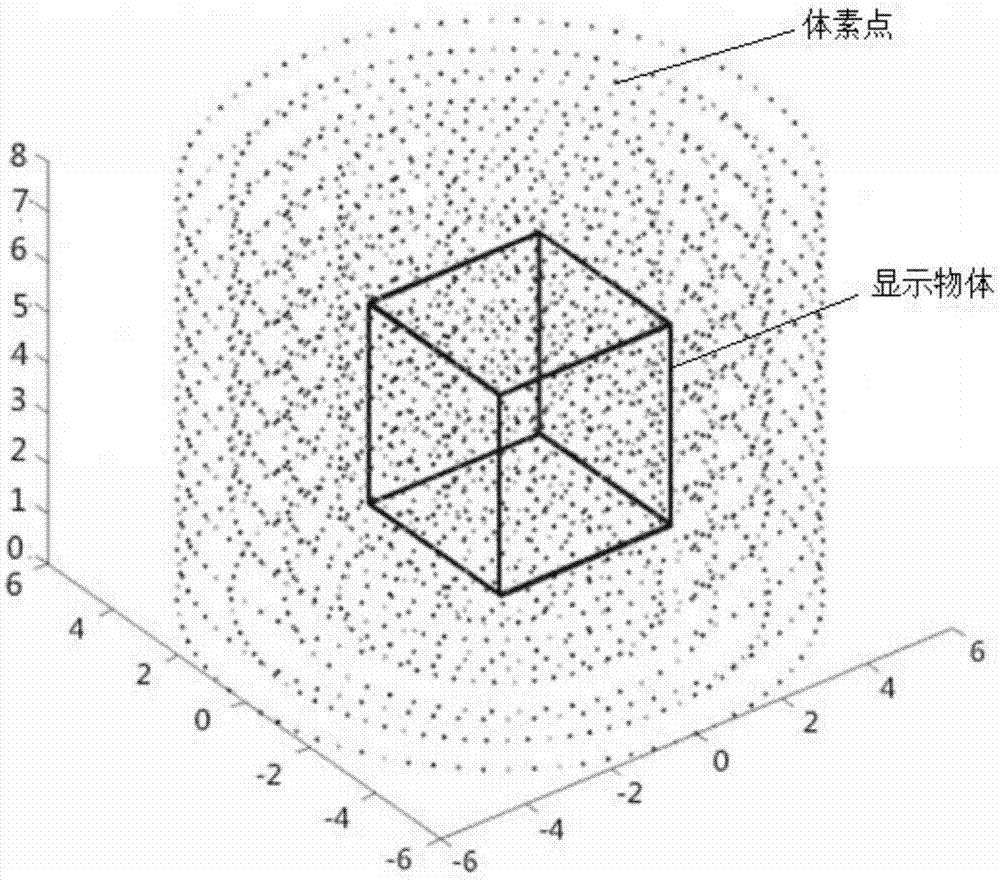
在真三维显示系统中，显示物体的每一个体素位于三维物理空间中的真实位置，且具有唯一的三维位置坐标和一维时间坐标。系统工作时，将原始三维图像数据转换成符合显示要求排列的体素点，送入显示单元，则每个体素点的亮度和色彩可控，体素点之间的相对空间位置关系被真实的体现，从而构成可直接观察的三维图像。

roesser模型是控制理论中最重要也是应用最广泛的模型之一，可以使用系统内部的状态变量来表征系统的动态特性。它由描述系统输出变量与状态变量间变换关系的输出方程组成。结合三维位置坐标与一维时间坐标，运用四维roesser模型对真三维显示系统进行状态空间表示，能够简化系统的数学表达式，反映系统中四个独立变量的变化，进而确定系统的全部内部运动状态，能够反映系统动态行为的全部信息。因此，找到roesser模型的实现方法，对真三维显示系统系统进行状态空间建模具有极高的应用价值。

现有的roesser模型实现方法有徐粒-阎石eoa变换法与ψ矩阵法。徐粒-阎石eoa变换法采用z1,z2,...,zn表示传递函数，引入eoa变换法给出了实现矩阵的求法，然而这种变换法中每次补充运算只能降低一阶。虽然可以通过一些分解来提高补充效率，但实际上只有极少数传递函数适用这种分解法。ψ矩阵法所求得的gr模型实现矩阵阶次更低，但不能分析系数值对实现矩阵的影响，因此不宜采用。

技术实现要素：

本发明为了解决现有技术存在的问题，提出一种基于真三维显示系统的roesser模型及其实现方法。

本发明的技术方案是：

基于真三维显示系统的roesser模型，其特征是，该模型为：在真三维显示系统中，将体素点的三维位置坐标与一维时间坐标结合，建立四维roessor状态空间模型，如下所示：

y(n1,n2,n3,t)＝cx(n1,n2,n3,t)+du(n1,n2,n3,t)

式中：

n1∈z，n2∈z，n3∈z，t∈z，向量x^h∈r^a，x^v∈r^b，x^l∈r^c，x^t∈r^d分别为x轴方向，y轴方向，z轴方向和时间t轴的向量；输入向量u∈r^p，输出向量y∈r^q；然后a1∈r^a×a，a2∈r^a×b，a3∈r^a×c，a4∈r^a×d，a5∈r^b×a，a6∈r^b×b，a7∈r^b×c，a8∈r^b×d，a9∈r^c×a，a10∈r^c×b，a11∈r^c×c，a12∈r^c×d，a13∈r^d×a，a14∈r^d×b，a15∈r^d×c，a16∈r^d×d，b1∈r^a×p，b2∈r^b×p，b3∈r^c×p，b4∈r^d×p，c∈r^q×(a+b+c+d)，d∈r^q×p。

在时隙t时，对于体素点(n1,n2,n3)，分别从体素(n1-1,n2,n3)、(n1,n2-1,n3)和(n1,n2,n3-1)接收状态向量组x^h(n1,n2,n3,t)，x^v(n1,n2,n3,t)和x^l(n1,n2,n3,t)；用roesser模型去计算向量x^h(n1+1,n2,n3,t)，x^v(n1,n2+1,n3,t)，x^l(n1,n2,n3+1,t)和x^t(n1,n2,n3,t+1)；发送向量x^h(n1+1,n2,n3,t)，x^v(n1,n2+1,n3,t)和x^l(n1,n2,n3+1,t)。

基于真三维显示系统的roesser模型的实现方法，其特征是，包括以下步骤：

步骤一，

令各系数矩阵：c＝[c1c2c3c4]，

根据传递函数的定义，该四维roesser模型的输出量y(n1,n2,n3,t)的z变换n(z1,z2,z3,z4)与输入量u(n1,n2,n3,t)的z变换d(z1,z2,z3,z4)之比：

对系统进行z变换，则系统对应的传递函数为：

h(z1,z2,z3,z4)＝cz(ir-az)^-1b+d(3)

其中，对角阵z＝diag{z1ia,z2ib,z3ic,z4id}，阶数r＝a+b+c+d；

根据因果性d＝0；

步骤二，定义四维多项式初始矩阵为

构造矩阵：

该矩阵应具有如下性质：

(a)对角线上第一个元素只能是x；

(b)对角线上其他元素只能是关于某一变量zk,k∈{1,2,3,4}的一维线性多项式，且常数项只能是1；

(c)除第一行外，非对角线元素只能为关于某一变量zk,k∈{1,2,3,4}的线性单项式；

(d)除x外，第一行中的元素均为常数项；

(e)同一行的元素只能包含同一个元素zk,k∈{1,2,3,4}，且从第二行开始，所有的行都是按照z1,z2,z3,z4的顺序排列的；

真三维显示系统的roesser模型实现方法即为通过矩阵初等变换和补充运算，将初始矩阵m0变换为m；

矩阵m0中对角线上第一个元素x在这里只是一个符号标志，而不是一个变量，在对初始矩阵m0变换的过程中，不能改变x的位置和表达式；这是因为，为了满足性质(a)和(b)，在对初始矩阵m0变换的过程中，不能对第一行进行任何变换运算，设置x就是为了阻止对第一行和第一列进行变换运算；

步骤三，设任意一不含常数项的四维多项式为p'(z1,z2,z3,z4)，对其中某个变量zk,k∈{1,2,3,4}显然可以分解成如下形式：

p'(z1,z2,z3,z4)＝p1(zk)+p2(z1,...,zk-1,zk+1,...,z4)+zkp3(z1,z2,z3,z4)(6)

其中，p1(zk)是只含有zk的一维线性多项式，p2(z1,...,zk-1,zk+1,...,z4)是不含有zk的四维线性多项式，且p1(zk)，p2(z1,...,zk-1,zk+1,...,z4)，p3(z1,z2,z3,z4)均不含常数项；

令则初始矩阵m0为

令根据式(6)，将和分解为

式中，p1和q1是只含z1的一维线性单项式，p2和q2是不含z1的三维线性多项式，p3和q3是四维多项式；

接着进行如下运算：

m1＝augment(m0)

m1＝addrow(m1,3,2,-z1)

m1＝addcol(m1,3,2,p3)

接着依次对p3、q3及m1中每次运算所产生的新的行进行运算，使得m1中含z1的项都变为关于z1的线性单项式；

m1中的每一行依次对变量z1、z2、z3、z4进行同样的运算，使得m1中除了x之外的对角线元素均为常数项为1的4维线性多项式，而除第一行外的非对角元素均为不含常数项的4维线性多项式；

步骤四，假设通过步骤一得到的矩阵m1为

式中，*和#都是线性多项式，ai,bi,ci,di,i＝{1,2,3,4}都是系数；

将第一步中所得到的矩阵m1转化成m2，使得m2中除x外的对角线元素均为常数项为1的一维线性多项式，而除第一行外的非对角元素均为关于某个变量zk,k∈{1,2,3,4}的线性单项式；

对式(10)中的m1进行如下运算

m2＝augment(m1)；

m2＝addrow(m2,4,2,-1)；

m2＝addcol(m2,4,1,a2z2)；

m2＝addcol(m2,4,2,b2z2)；

在同一行中，对变量z3,z4进行相似的运算，最终得到矩阵m2，使得m2中第二行的前三个元素分别为a1z1，1+b1z1和c1z1，其余元素均为-1；

步骤五，通过适当的行变换和列变换，将m2中的每一行按照z1、z2、z3、z4的顺序排列，并将所有的一维线性多项式元素移到对角线位置，再通过列变换消去-1项，得到矩阵m3；

根据式(5)得出矩阵a,b,c。

本发明的有益效果：

本发明运用四维roesser模型对真三维显示系统进行状态空间表示，可以表征和计算体素变量，使得在时隙t计算的各变量只与相邻的前一体素或前一时刻有关，从而能够简化运算，便于微控制器的软件实现。

与徐粒-阎石eoa变换法eoa变换法相比，本发明的四维roesser模型实现方法得到的实现矩阵阶次更低，又克服了ψ矩阵法不能分析系数值对实现矩阵的影响的缺点，因此既能简化系统数学表达，又有利于系统分析与设计，具有极高的应用价值。

附图说明

图1是本发明基于真三维显示系统的roesser模型示意图。

具体实施方式

下面结合附图对本发明做进一步详细说明。

如图1所示，基于真三维显示系统的roesser模型，该模型为：在真三维显示系统中，显示物体的体素点按显示要求有序排列，且具有唯一的三维位置坐标和一维时间坐标，将体素点的三维位置坐标与一维时间坐标结合，建立四维roessor状态空间模型，如下所示：

y(n1,n2,n3,t)＝cx(n1,n2,n3,t)+du(n1,n2,n3,t)

式中：

n1∈z，n2∈z，n3∈z，t∈z，向量x^h∈r^a，x^v∈r^b，x^l∈r^c，x^t∈r^d分别为x轴方向，y轴方向，z轴方向和时间t轴的向量。输入向量u∈r^p，输出向量y∈r^q。然后a1∈r^a×a，a2∈r^a×b，a3∈r^a×c，a4∈r^a×d，a5∈r^b×a，a6∈r^b×b，a7∈r^b×c，a8∈r^b×d，a9∈r^c×a，a10∈r^c×b，a11∈r^c×c，a12∈r^c×d，a13∈r^d×a，a14∈r^d×b，a15∈r^d×c，a16∈r^d×d，b1∈r^a×p,b2∈r^b×p，b3∈r^c×p，b4∈r^d×p，c∈r^q×(a+b+c+d)，d∈r^q×p。

在时隙t时，对于体素点(n1,n2,n3)，分别从体素(n1-1,n2,n3)、(n1,n2-1,n3)和(n1,n2,n3-1)接收状态向量组x^h(n1,n2,n3,t)，x^v(n1,n2,n3,t)和x^l(n1,n2,n3,t)；用roesser模型去计算向量x^h(n1+1,n2,n3,t)，x^v(n1,n2+1,n3,t)，x^l(n1,n2,n3+1,t)和x^t(n1,n2,n3,t+1)；发送向量x^h(n1+1,n2,n3,t)，x^v(n1,n2+1,n3,t)和x^l(n1,n2,n3+1,t)。

基于真三维显示系统的roesser模型的实现方法，包括以下步骤：

步骤一，

令各系数矩阵：c＝[c1c2c3c4]，

对系统进行z变换，则系统对应的传递函数为：

h(z1,z2,z3,z4)＝cz(ir-az)^-1b+d(2)

其中，对角阵z＝diag{z1ia,z2ib,z3ic,z4id}，阶数r＝a+b+c+d。

根据传递函数的定义，该四维roesser模型的输出量y(n1,n2,n3,t)的z变换n(z1,z2,z3,z4)与输入量u(n1,n2,n3,t)的z变换d(z1,z2,z3,z4)之比：

每个体素点的显示是一个线性过程，由于物体的三维数学模型一定可实现可观测，即是一个因果过程，则整个体素空间的显示过程是一个第一卦限上的线性因果关系的过程，所以d＝0。

令m表示一个矩阵，定义以下符号表示的操作为：

addrow(m,i,j,k)：将矩阵m的第i行所有元素乘以k后加到第j行对应的元素上；

addcol(m,i,j,k)：将矩阵m的第i列所有元素乘以k后加到第j列对应的元素上；

swaprow(m,i,j)：交换矩阵m的第i行和第j行对应的元素；

swapcol(m,i,j)：交换矩阵m的第i列和第j列对应的元素；

步骤二，定义四维多项式初始矩阵为：

构造矩阵：

该矩阵具有如下特点：

(a)对角线上第一个元素只能是x；

(b)对角线上其他元素只能是关于某一变量zk,k∈{1,2,3,4}的一维线性多项式，且常数项只能是1；

(c)除第一行外，非对角线元素只能为关于某一变量zk,k∈{1,2,3,4}的线性单项式；

(d)除x外，第一行中的元素均为常数项；

(e)同一行的元素只能包含同一个元素zk,k∈{1,2,3,4}，且从第二行开始，所有的行都是按照z1,z2,z3,z4的顺序排列的。

真三维显示系统的roesser模型实现方法即为通过矩阵初等变换和补充运算，将初始矩阵m0变换为m。

矩阵m0中对角线上第一个元素x在这里只是一个符号标志，而不是一个变量，在对初始矩阵m0变换的过程中，不能改变x的位置和表达式。这是因为，为了满足性质(a)和(b)，在对初始矩阵m0变换的过程中，不能对第一行进行任何变换运算，设置x就是为了阻止对第一行和第一列进行变换运算。

步骤三，设任意一不含常数项的四维多项式为p'(z1,z2,z3,z4)，对其中某个变量zk,k∈{1,2,3,4}显然可以分解成如下形式：

p'(z1,z2,z3,z4)＝p1(zk)+p2(z1,...,zk-1,zk+1,...,z4)+zkp3(z1,z2,z3,z4)(7)

其中，p1(zk)是只含有zk的一维线性多项式，p2(z1,...,zk-1,zk+1,...,z4)是不含有zk的四维线性多项式，且p1(zk)，p2(z1,...,zk-1,zk+1,...,z4)，p3(z1,z2,z3,z4)均不含常数项。

令则初始矩阵m0为

令根据式(7)，将和分解为

式中，p1和q1是只含z1的一维线性单项式，p2和q2是不含z1的三维线性多项式，p3和q3是四维多项式。

接着进行如下运算：

m1＝augment(m0)

m1＝addrow(m1,3,2,-z1)

m1＝addcol(m1,3,2,p3)

接着依次对p3、q3及m1中每次运算所产生的新的行进行运算，使得m1中含z1的项都变为关于z1的线性单项式。

m1中的每一行依次对变量z1、z2、z3、z4进行同样的运算，使得m1中除了x之外的对角线元素均为常数项为1的4维线性多项式，而除第一行外的非对角元素均为不含常数项的4维线性多项式。

步骤四，假设通过步骤一得到的矩阵m1为

式中，*和#都是线性多项式，ai,bi,ci,di,i＝{1,2,3,4}都是系数。

将第一步中所得到的矩阵m1转化成m2，使得m2中除x外的对角线元素均为常数项为1的一维线性多项式，而除第一行外的非对角元素均为关于某个变量zk,k∈{1,2,3,4}的线性单项式。

对式(11)中的m1进行如下运算

m2＝augment(m1)；

m2＝addrow(m2,4,2,-1)；

m2＝addcol(m2,4,1,a2z2)；

m2＝addcol(m2,4,2,b2z2)；

在同一行中，对变量z3,z4进行相似的运算，最终得到矩阵m2，使得m2中第二行的前三个元素分别为a1z1，1+b1z1和c1z1，其余元素均为-1。

步骤五，通过适当的行变换和列变换，将m2中的每一行按照z1、z2、z3、z4的顺序排列，并将所有的一维线性多项式元素移到对角线位置，再通过列变换消去-1项，得到矩阵m3。

根据式(5)得出矩阵a,b,c。

实施例：

已知严密因果传递函数：

由严密因果性，得：d＝h(0,0,0,0)＝0。

构造初始矩阵：

对其做如下变换：

m1＝augment(m0)

m1＝addrow(m1,3,2,-z1)

m1＝addcol(m1,3,1,z2+z3+z4)

m2＝augment(m1)

m2＝addrow(m2,4,2,-z2)

m2＝addcol(m2,4,2,z3)

m3＝augment(m2)

m3＝addrow(m3,5,2,-1)

m3＝addcol(m3,5,4,-z2)

m4＝augment(m3)

m4＝addrow(m4,6,3,-1)

m4＝addcol(m4,6,1,z3+z4)

m4＝addcol(m4,6,2,z3+z4)

m5＝augment(m4)

m5＝addrow(m5,7,6,-1)

m5＝addcol(m5,7,1,z4)

m5＝addcol(m5,7,2,z4)

m5＝swaprow(m5,4,5)

m5＝swapcol(m5,4,5)

m5＝addcol(m5,2,4,1)

m5＝addcol(m5,3,6,1)

得：

根据式(12)，得：a＝1,b＝2,c＝2,d＝1，即实现矩阵的阶数r＝6。

c＝[110011],d＝0。