一种基于预测-校正模型的网格简化方法与流程

本发明属于计算机图形学领域，涉及三维网格简化技术，特别是涉及一种基于预测-校正模型的网格简化方法。

背景技术

在计算机中，三维模型通常表示为面模型或者体模型；其中，使用多边形网格尤其是三角网格的面模型最为常用，这种模型的通用性和灵活性比较好，而且数学表示简单。随着人们对于图像质量要求的提高，网格模型复杂度也随之提高，即便是一个非常简单的模型，可能也需要上万个三角面来描述，因此网格模型简化算法的研究显得尤为重要。

目前基于三角网格的简化方法有许多种，根据原理的不同大致可以分为顶点删除法、顶点聚类法、边折叠法和面折叠法等。其中，边折叠法使用最为广泛。garland等提出基于qem(quadricerrormetrics，二次误差测度)的简化算法，其误差测度为顶点到平面的距离平方和，优点为计算速度快，生成网格较为平均，是一种非常有效的化简算法。但此方法会在边折叠过程中引入折叠误差，并造成误差的累积。

技术实现要素：

为解决上述问题，本发明公开了一种基于预测-校正模型的网格简化方法，通过校正边折叠过程中新顶点的二次误差矩阵，能够有效的控制简化过程中的累积误差。

为了达到上述目的，本发明提供如下技术方案：

一种基于预测-校正模型的网格简化方法，包括如下步骤：

第一步，读取三维网格中所有的顶点和面，计算其基础二次方矩阵和二次误差矩阵；

第二步，计算出所有边的初始折叠误差和对应的新顶点的位置，并将初始折叠误差插入优先队列中；

第三步，从优先队列中选择折叠误差最小的一条边，进行一次折叠操作，并更新相关的顶点和面；

第四步，根据新顶点的位置，重新计算相邻面的基础二次方矩阵和新顶点的二次误差矩阵；

第五步，重新计算与折叠点相邻的边的折叠误差和对应的新顶点的位置，更新优先队列；

第六步，判断是否满足简化条件，若不满足，则返回第三步；若满足，则过程结束。

进一步的，第一步包括如下过程：

通过下式计算每个面的基础二次方矩阵kp，存入对象的属性中：

其中，p＝[abcd]^t代表了平面：

ax+by+cz+d＝0(a²+b²+c²＝1)

a、b、c由面的单位法向量得到，d＝-(ax+by+cz)；

将计算获得的矩阵kp保存在顶点的属性中；

通过下式计算所有顶点的二次误差矩阵q：

其中planes(v)代表了与顶点v相邻的所有面，最终将计算获得的q保存在顶点的属性中。

进一步的，第二步中新顶点位置和折叠误差的计算方法如下：

通过下式计算新顶点的二次误差矩阵的估计值

判断矩阵

是否可逆，其中，qij是矩阵中的项；

如果矩阵不可逆，则从折叠边的两个端点v1、v2或中点(v1+v2)/2中选择折叠代价最小的作为折叠新顶点；如果矩阵可逆，则计算出该新顶点的位置为：

通过下式计算折叠误差：

进一步的，所述第三步更新相关顶点和面的过程中包括以下过程：

获取顶点v1，v2所有相邻的面，删除共有的面，将其他面中的顶点v1，v2替换为新顶点

获取顶点v1，v2所有相邻的顶点，更新这些顶点的相邻顶点列表，用新顶点代替v1，v2，并同时更新新顶点的相邻顶点列表。

进一步的，所述第三步中使用costheap的delmin()方法获得折叠代价最小的一条边。

进一步的，所述第四步包括以下过程：

针对折叠后的新顶点重新计算与其相邻的面的基础二次方矩阵：

重新计算顶点的二次误差矩阵：

使用上式中的取代第二步中二次误差矩阵的预测值

进一步的，所述第五步使用与第二步相同的方法重新计算与新顶点相邻的边的折叠误差和对应的折叠点的位置。

进一步的，所述第六步中的简化条件为顶点数或简化比例。

与现有技术相比，本发明具有如下优点和有益效果：

本发明采用预测-校正的思想进行边折叠，与原有方法相比，新顶点的二次误差矩阵由更新后的邻接面计算而来，而不是直接由两个端点的二次误差矩阵相加得到。基于此，本发明能够在快速高效的精简网格的同时，有效的控制边折叠过程中的累积误差，改善简化模型的质量，尤其是对于细节的保留效果突出，有较强的通用性，相较于传统方法能够取得更为突出的简化效果，从而提升整体的简化效果。

附图说明

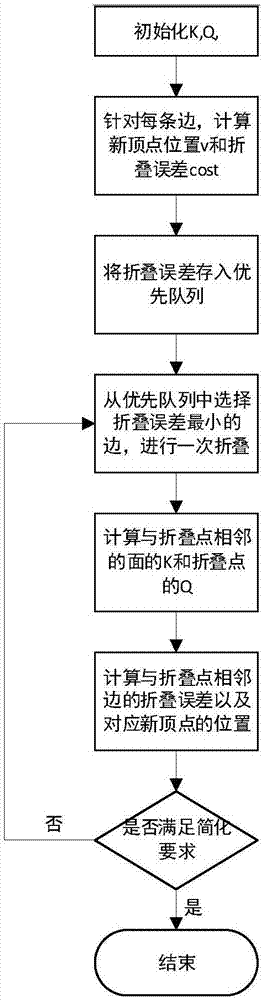
图1为本发明提供的一种基于预测-校正模型的网格简化方法的流程图。

图2为采用qem算法和本发明方法对dinosaur模型进行简化的效果对比图；其中(a)为原模型；(b)为采用qem算法对原模型简化后效果图，简化比例50％；(c)为采用qem算法对原模型简化后效果图，简化比例10％；(d)为采用本发明方法对原模型简化后效果图，简化比例50％；(e)为采用本发明方法对原模型简化后效果图，简化比例10％。

图3为图2中qem算法和本发明方法在简化比例α＝0.1时局部细节放大比较图，其中(a)为qem算法细节放大图，(b)为本发明方法放大图。

图4为采用qem算法和本发明方法对castle模型进行简化的效果对比图；其中(a)为原模型；(b)为采用qem算法对原模型简化后效果图，简化比例10％；(c)为采用本发明方法对原模型简化后效果图，简化比例10％。

具体实施方式

以下将结合具体实施例对本发明提供的技术方案进行详细说明，应理解下述具体实施方式仅用于说明本发明而不用于限制本发明的范围。

本实施例采用java作为编程语言，如图1所示，本实施例采用如下步骤：

步骤1，读取三维网格中所有的顶点和面计算基础二次方矩阵kp和二次误差矩阵q。

定义p＝[abcd]^t代表了平面：

ax+by+cz+d＝0(a²+b²+c²＝1)

a、b、c可以由面的单位法向量得到；d＝-(ax+by+cz)，通过代入面的一个顶点坐标，可以获得d的值。

使用距离的平方作为误差的度量，折叠点v的误差可以写作：

其中planes(v)代表了与顶点v相邻的所有面，将其写成二次型的形式：

其中，kp是平面p的基础二次方矩阵：

建立两个类vertex和face，用来对应模型中的顶点和面。对三维obj文件进行解析，读取网格三维网格中所有的顶点和面，分别建立两个arraylist：vertexlist用于保存顶点，facelist用于保存面。在解析的同时，保存与顶点相邻的顶点和面的信息，存入vertex属性中的顶点邻接表和面邻接表中。

首先遍历facelist，对其中的每一个face对象(即所有面)计算基础二次方矩阵kp，存入对象的属性中，将计算获得的矩阵kp保存在顶点的属性中。

接着遍历顶点的列表vertexlist，计算所有顶点的二次误差矩阵q，某一顶点v的初始二次误差矩阵定义为相邻面基础二次方矩阵乘以面积约束因子的和，即初始二次误差矩阵为：

最终将计算获得的q保存在顶点的属性中。

步骤2，在顶点的数据结构中包括与其相邻的待折叠的边的另一个顶点，最小的折叠代价以及新顶点的位置，这样就可以将所有边的折叠代价作为顶点的属性保存在顶点的数据结构中。本步骤对于列表vertexlist中的每个顶点vertex，遍历与其相邻的所有顶点，从而遍历两个顶点之间构成的与顶点vertex相邻的边，计算边的折叠代价。计算方法为：

在计算每条边的初始折叠误差时，使用边的两个顶点的二次误差矩阵之和作为新顶点的二次误差矩阵的估计值，并以此计算新顶点的位置。即对于边两个顶点v1，v2，在步骤1中已经计算出了其二次误差矩阵q(v1)和q(v2)，计算判断矩阵

是否可逆。其中，qij是矩阵中的项。如果矩阵不可逆，则从折叠边的两个端点v1、v2或中点(v1+v2)/2中选择折叠代价最小的作为折叠新顶点。如果矩阵可逆，则可以计算出该新顶点的位置为：

则折叠所产生的误差(即折叠代价)为：

将该误差插入到优先队列中，同时记录相应的顶点索引，以便后续步骤引用。

步骤3，使用costheap的delmin()方法获得折叠代价最小的一条边，对其进行折叠操作，并更新相关顶点和面的属性。对于一次折叠操作其新顶点的坐标由上一步计算得到。在一次边折叠后，要更新与该边关联的所有顶点和面的拓扑关系，进行局部网格重构，具体如下：

分别使用两个列表记录与原顶点v1,v2相邻的所有的面和所有的顶点。删除与原顶点v1,v2所有相邻的面，重新建立新顶点到所有相邻顶点的连接。更新相关顶点的顶点邻接表(保存相邻顶点信息)和面邻接表(保存相邻面信息)。

步骤4，查询新顶点的面邻接表，计算所有面的基础二次方矩阵kp：

再计算顶点的二次误差矩阵：

使用计算出的二次误差矩阵q取代之前的预测值将其存入顶点的属性中。

步骤5，查询新顶点的顶点邻接表，重新计算与相邻的所有边的折叠误差以及对应的新顶点的位置。计算方法与步骤2中所述方法相同。将计算后的结果重新插入优先队列中。

步骤6，判断是否满足设定的简化条件，本例中简化条件设置为判断网格当前的顶点数是否小于设定的顶点数n。若顶点数大于n，则返回步骤3；若顶点数小于等于n，则算法结束。简化条件可以为其他条件，如简化比例等。

为了说明本发明中算法的有效性，我们分别对多个模型使用qem算法和本发明方法进行简化，对比简化后的结果。

图2是dinosaur模型的简化效果对比。图2(a)是原始模型，包含了约2000个顶点和3000个面。图(b)和图(c)分别是使用qem算法将模型的顶点数简化至原来的50％和10％的效果，图(d)和图(e)则是使用本发明方法将模型的顶点数简化至原来的50％和10％的效果。

从图中可以看出，当简化的比例较小(50％)的时候，两种算法都能得到非常好的简化效果，细节特征都得到了很好的保留，几乎无法看出它们与原模型的区别。但是当简化的比例较大(10％)的时候，两种算法还是显示出了区别。qem算法生成的网格较为平均，保证了模型的整体效果，但是这也导致了其在平坦的区域使用了较多的三角形(背部和腹部)，从而使一些明显的特征保留不够，如恐龙模型的眼睛区域；而改进后的方法在恐龙面部和腿部使用了更多的三角形，因此对细节特征的保留更好，如图3所示。

图4是castle模型的简化效果对比。图4(a)是原始模型，包含约3000个顶点和6000个面。图4(b)和图4(c)分别是使用qem算法和本文的算法对原模型简化到顶点数的10％的效果图。此模型与dinosaur模型相比，存在许多曲率剧烈变化的表面，因此特征更为突出。可以发现，在图(c)中，城堡的角旗部分使用了更多的三角形，因此特征保留更为完整；而在原本相对平整的城墙部分使用的三角形更少，整体的简化效果也更好。

本方案在算法复杂度上，由于三角面的面积可以非常容易的获得，计算新顶点的二次误差矩阵也可以在常数时间内完成，所以时间复杂度与qem算法相同，均为o(nlogn)，并不会显著增加运行时间。

本发明方案所公开的技术手段不仅限于上述实施方式所公开的技术手段，还包括由以上技术特征任意组合所组成的技术方案。应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也视为本发明的保护范围。